Natężenie pola elektrycznego – zadanie nr 3

Oblicz natężenie pola elektrycznego w punkcie P o współrzędnych (5,4), jeżeli ładunek o wartości q  = 2 ⋅ 10^-5 C umieszczono w punkcie (1,1). Jednostką na każdej osi układu współrzędnych jest 1 m.

(Zadanie ze zbioru: K. Chyła Zbiór prostych zadań z fizyki dla uczniów szkół średnich)

Zacznijmy od sporządzenia rysunku przedstawiającego sytuację opisaną w treści zadania:

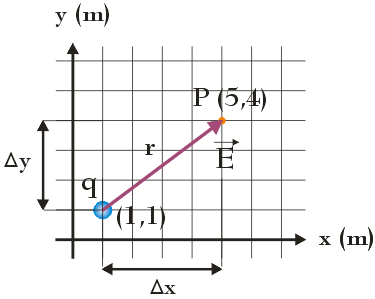
Ładunek q  jest ładunkiem dodatnim, w związku z czym natężenie pola elektrycznego $\vec{E}$  jest skierowane od tego ładunku. Aby obliczyć wartość natężenia pola elektrycznego w punkcie P musimy zgodnie z poniższym wzorem znać wartość ładunku q  oraz odległość r  dzielącą ten ładunek od punktu P:

$$E = k \hspace{.05cm} \frac{q}{r^2}$$

Odległość r  nie jest podana w treści zadania. Możemy ją jednak z łatwością obliczyć, ponieważ zgodnie z powyższym rysunkiem odległość tą możemy wyrazić jako (korzystamy z twierdzenia Pitagorasa):

$$r^2 = \left( \Delta \hspace{.03cm} x \right)^2 + \left( \Delta \hspace{.03cm} y \right)^2$$

gdzie Δx  i Δy  to odległość dzieląca ładunek q  od punktu P wzdłuż linii równoległej odpowiednio do osi OX i OY: Δx  = x_p  – x_q , Δy  = y_p – y_q .

Ponieważ x_p  = 5 m, x_q  = 1 m, y_p  = 4 m, y_q  = 1 m, dlatego Δx  = 4 m, a Δy  = 3 m. Podstawiając te wartości do wzoru na r², dostaniemy:

$$r^2 = \left( 4 \hspace{.03cm} \textrm{m} \right)^2 + \left( 3 \hspace{.03cm} \textrm{m} \right)^2 = 25 \hspace{.05cm} \textrm{m}^2$$

Po wstawieniu do wzoru $E = k \dfrac{q}{r^2}$ wartości liczbowych k  (k  = 9 ⋅ 10⁹ N ⋅ m²/C²), q  i r² oraz wykonaniu obliczeń, dostaniemy wartość natężenia pola elektrycznego, równą:

$$E = 9 \cdot 10^9 \hspace{.05cm} \tfrac{\textrm{N} \hspace{.05cm} \cdot \hspace{.05cm} \textrm{m}^2}{\textrm{C}^2} \cdot \frac{2 \cdot 10^{-5} \hspace{.05cm} \textrm{C}}{25 \hspace{.05cm} \textrm{m}^2} = 7200 \hspace{.05cm} \tfrac{\textrm{N}}{\textrm{C}}$$