Fale mechaniczne – opis. Amplituda, faza, liczba falowa, okres, częstotliwość, częstość kołowa i prędkość fali

W tym artykule zajmiemy się opisem wielkości fizycznych charakteryzujących fale mechaniczne. Za przykład posłuży nam fala poprzeczna wytworzona w linie, czyli fala, w której drgania ośrodka (w tym przypadku drgania elementów liny) zachodzą w kierunku prostopadłym do kierunku rozchodzenia się fali. Wzory, które znajdziesz w dalszej części tego artykułu będzie można zastosować nie tylko do opisu mechanicznych fal poprzecznych, ale także do opisu mechanicznych fal podłużnych (np. fal dźwiękowych). A zatem do dzieła!

Jak wytworzyć i opisać mechaniczną falę poprzeczną?

Gdy złapiemy jeden koniec napiętej liny i zaczniemy poruszać nim w sposób ciągły w górę i w dół ruchem harmonicznym, to efektem tych działań będzie powstanie ciągłego zaburzenia kształtu liny poruszającego się wzdłuż niej z pewną prędkością. To zaburzenie kształtu liny to nic innego tylko fala. Zgodnie z poniższym rysunkiem elementy liny poruszają się prostopadle do kierunku rozchodzenia się fali, w związku z czym fala wytworzona w linie jest falą poprzeczną.

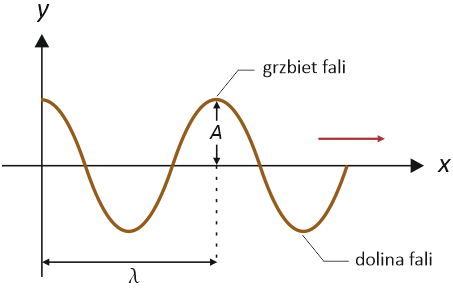
Aby móc powiedzieć coś więcej na temat tej fali, musimy zacząć od znalezienia funkcji, która pozwoli nam opisać jej kształt. Funkcja ta musi opisywać poprzeczne przemieszczenie y  elementu liny w zależności od położenia x  elementu liny oraz od czasu t. Patrząc na powyższy rysunek nietrudno się domyślić, że kształt fali wytworzonej w linie może być opisany za pomocą jednej z dwóch podstawowych funkcji trygonometrycznych tj. funkcji sinus albo funkcji cosinus. Ponieważ w artykule Ruch harmoniczny – opis przyjęliśmy, że wychylenie ciała z położenia równowagi będziemy opisywać przy pomocy funkcji cosinus, to i w tym przypadku postąpimy tak samo. Gdy fala wytworzona w linie porusza się w dodatnim kierunku osi x  (czyli tak jak na powyższym rysunku), przemieszczenie y  elementu liny w punkcie x  w chwili t, wynosi:

$$y \hspace{.05cm} (x, t) = A \hspace{.1cm} \textrm{cos} \left( k \hspace{.05cm} x \hspace{.15cm} – \hspace{.1cm} \omega \hspace{.05cm} t \right)$$

gdzie:
A  – amplituda fali,
kx  – ωt  – faza fali,
k  – liczba falowa,
ω  – częstość kołowa.

(w przypadku fali poruszającej się w ujemnym kierunku osi x  faza fali będzie równa kx  + ωt )

Amplituda fali

Amplitudą fali A  nazywamy bezwzględną wartość maksymalnego przemieszczenia elementu ośrodka (w naszym przykładzie elementu liny) względem jego położenia równowagi. Zwróć uwagę, że zgodnie z rysunkiem maksymalne przemieszczenie elementu liny występuje zarówno w dodatniej, jak i ujemnej połówce kosinusoidy. Ze względu na ten fakt interesuje nas właśnie bezwzględna wartość A (dzięki temu A  zawsze będzie dodatnie). Jednostką amplitudy w układzie SI jest jednostka długości, czyli metr (m).

Faza fali

Fazą fali nazywamy argument kx  – ωt  funkcji cosinus występującej w wyrażeniu opisującym przemieszczenie y  elementu liny. Faza fali ulega zmianie wraz ze zmianą położenia x  oraz czasu t. Korzystając z własności funkcji cosinus możemy stwierdzić, że wartość wyrażenia cos (kx – ωt ) zmienia się w przedziale [-1, +1]. Wartość cos (kx – ωt ) = 1 odpowiada grzbietowi fali przechodzącemu przez element ośrodka (przemieszczenie y  = 1), z kolei wartość cos (kx – ωt ) = -1 – dolinie fali (przemieszczenie y  = -1).

Liczba falowa i długość fali

Długość fali λ  to odległość między kolejnymi powtórzeniami kształtu fali, mierzona równolegle do kierunku rozprzestrzeniania się fali. Jednostką długości fali w układzie SI jest jednostka długości, czyli metr (m).

Wielkość k  występująca w wyrażeniu kx  – ωt  nazywana jest liczbą falową. Wielkość ta zdefiniowana jest następująco:

$$k = \dfrac{2 \hspace{.05cm} \pi}{\lambda}$$

Jednostką liczby falowej w układzie SI jest radian na sekundę (rad/s).

Okres i częstość kołowa fali

Okres T  to czas, w którym dowolny element ośrodka (np. element liny) wykonuje jedno pełne drganie. Jednostką okresu w układzie SI jest jednostka czasu, czyli sekunda (s).

Wielkość ω  występująca w wyrażeniu kx  – ωt  to częstość kołowa fali, opisująca szybkość, z jaką powtarza się jedno pełne drganie elementu ośrodka. Wielkość ta związana jest z okresem ruchu T następującą zależnością:

$$\omega = \frac{2 \hspace{.05cm} \pi}{T}$$

Jednostką częstości kołowej w układzie SI jest radian na sekundę (rad/s).

Częstotliwość fali

Odwrotnością okresu T  jest częstotliwość f  opisująca liczbę pełnych drgań elementu ośrodka wykonywanych podczas każdej sekundy ruchu ciała. Częstotliwość f  jest równa:

$$f = \frac{1}{T}$$

Jednostką częstotliwości w układzie SI jest herc (Hz), związany z jednostką czasu – sekundą – poniższą zależnością:

$$1 \hspace{.05cm} \textrm{Hz} = \frac{1}{\textrm{s}}$$

Po podstawieniu zależności wiążącej okres T  z częstotliwością f  do wyrażenia na częstość kołową ω, otrzymamy:

$$\omega = \frac{2 \hspace{.05cm} \pi}{T} = 2 \hspace{.05cm} \pi \hspace{.05cm} f$$

Prędkość fali

Prędkość V, z jaką fala rozchodzi się w ośrodku możemy obliczyć z poniższego wzoru:

$$V = \dfrac{\omega}{k}$$

Ponieważ $\omega = 2 \hspace{.05cm} \pi \hspace{.05cm} f$,  a  $k = \dfrac{2 \hspace{.05cm} \pi}{\lambda}$,  mamy:

$$V = \dfrac{2 \hspace{.05cm} \pi \hspace{.05cm} f}{\dfrac{2 \hspace{.05cm} \pi}{\lambda}} = \lambda \hspace{.05cm} f$$

Jednostką prędkości fali w układzie SI jest metr na sekundę (m/s).