Zwierciadło płaskie, wklęsłe i wypukłe – zadanie nr 2

Oblicz w jakiej odległości od zwierciadła sferycznego wklęsłego o promieniu krzywizny r  = 0,4 m należy umieścić przedmiot P, aby na ekranie odległym o y  = 2,5 m od zwierciadła otrzymać obraz tego przedmiotu?

Położenie, rodzaj oraz orientacja obrazu przedmiotu wytwarzanego przez zwierciadło sferyczne wklęsłe zależy od położenia tego przedmiotu względem środka zwierciadła wklęsłego. Aby otrzymać obraz przedmiotu po tej samej stronie zwierciadła, po której znajduje się przedmiot (czyli tak jak w naszym zadaniu), należy, zgodnie z teorią umieścić ten przedmiot za ogniskową f  zwierciadła.

Aby obliczyć w jakiej odległości od środka zwierciadła s  należy umieścić przedmiot P, skorzystamy z poniższego wzoru:

$$\frac{1}{x} + \frac{1}{y} = \frac{1}{f}$$

gdzie:
x  – odległość przedmiotu od środka zwierciadła,
y  – odległość obrazu od środka zwierciadła,
f  – ogniskowa zwierciadła.

Odległość y  jest znana. Wartość ogniskowej f  nie jest podana. Możemy ją jednak z łatwością obliczyć, ponieważ znamy promień krzywizny r  zwierciadła. Zależność pomiędzy r  a f  przedstawia się następująco:

$$f = \tfrac{1}{2} \hspace{.05cm} r$$

Wstawiając tą zależność do pierwszego równania (w miejsce f ), otrzymamy:

$$\frac{1}{x} + \frac{1}{y} = \frac{1}{\tfrac{1}{2} \hspace{.05cm} r}$$

Po przekształceniu powyższego wyrażenia względem szukanej odległości x , dostaniemy:

$$\frac{1}{x} = \frac{1}{\tfrac{1}{2} \hspace{.05cm} r} \hspace{.1cm} – \hspace{.1cm} \frac{1}{y} = \frac{y \hspace{.15cm} – \hspace{.05cm} \tfrac{1}{2} \hspace{.05cm} r}{\tfrac{1}{2} \hspace{.05cm} r \hspace{.05cm} y} = \frac{2 \hspace{.05cm} y \hspace{.1cm} – \hspace{.1cm} r}{y \hspace{.05cm} r}$$

i po odwróceniu stronami:

$$x = \frac{y \hspace{.05cm} r}{2 \hspace{.05cm} y \hspace{.1cm} – \hspace{.1cm} r}$$

Po wstawieniu do powyższego wzoru wartości liczbowych podanych w treści zadania otrzymamy odległość x  równą:

$$x = \frac{2,\hspace{-.1cm}5 \hspace{.05cm} \textrm{m} \cdot 0,\hspace{-.1cm}4 \hspace{.05cm} \textrm{m}}{2 \cdot 2,\hspace{-.1cm}5 \hspace{.05cm} \textrm{m} \hspace{.1cm} – \hspace{.1cm} 0,\hspace{-.1cm}4 \hspace{.05cm} \textrm{m}} = \frac{1 \hspace{.05cm} \textrm{m}^2}{4,\hspace{-.1cm}6 \hspace{.1cm} \textrm{m}} = 0,\hspace{-.1cm}22 \hspace{.1cm} \textrm{m}$$

Zauważ, że odległość x , zgodnie z tym co napisaliśmy wyżej, przyjmuje większą wartość, niż ogniskowa f  zwierciadła (f  = 1/2 r  = 0,2 m), co oznacza, że otrzymany wynik jest wynikiem prawidłowym.

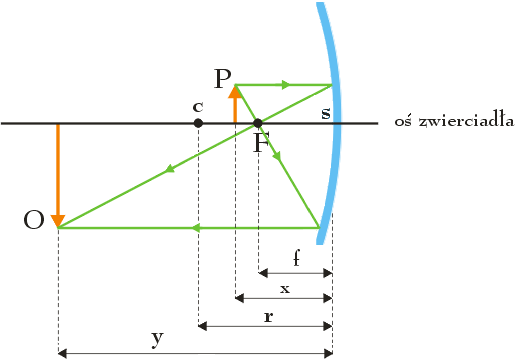
Obraz przedmiotu utworzony na ekranie, zgodnie z poniższym rysunkiem, jest obrazem rzeczywistym, odwróconym i powiększonym (odległości x , y , r  i f  nie odpowiadają tym podanym w treści zadania):