Szeregowe i równoległe łączenie rezystorów – zadanie nr 4

Oblicz opór zastępczy R_Z  układu oporników przedstawionych na poniższym rysunku wiedząc, że rezystancja oporników wynosi: R₁ = 3 Ω, R₂ = 4 Ω, R₃ = 7 Ω, R₄ = 10 Ω, R₅ = 5 Ω i R₆ = 2 Ω.

Przed przystąpieniem do obliczenia oporu zastępczego R_Z  oporników, określmy na początku sposób ich połączenia w obwodzie. Zwróć uwagę, że początki oraz końce rezystorów R₁ i R₂ oraz R₅ i R₆ połączone są za pomocą wspólnych przewodów, co oznacza, że oporniki te są połączone równolegle. Oporniki R₃ i R₄ są z kolei ustawione jeden za drugim, a więc, zgodnie z teorią, są połączone w sposób szeregowy (zobacz: Szeregowe i równoległe łączenie rezystorów). W oparciu o te informacje możemy zająć się obliczeniem oporu zastępczego R_Z . Sposób w jaki to zrobimy, zależy oczywiście od nas. My skupimy się tutaj na obliczeniu składowych oporów dla rezystorów połączonych równolegle, by później, po uproszczeniu obwodu, wyznaczyć R_Z  ze wzoru na połączenie szeregowe oporników.

Zajmijmy się więc obliczeniem oporu zastępczego dla rezystorów R₁ i R₂ oraz R₅ i R₆. Jak napisaliśmy wcześniej, rezystory te są połączone równolegle, dlatego też:

$$\frac{1}{R_{12}} = \frac{1}{R_1} + \frac{1}{R_2}$$

oraz

$$\frac{1}{R_{56}} = \frac{1}{R_5} + \frac{1}{R_6}$$

Zgodnie z treścią zadania R₁ = 3 Ω, R₂ = 4 Ω, R₅ = 5 Ω i R₆ = 2 Ω, w związku z czym:

$$\frac{1}{R_{12}} = \frac{1}{3 \hspace{.05cm} \Omega} + \frac{1}{4 \hspace{.05cm} \Omega} = \frac{4}{12 \hspace{.05cm} \Omega} + \frac{3}{12 \hspace{.05cm} \Omega} = \frac{7}{12 \hspace{.05cm} \Omega}$$

oraz

$$\frac{1}{R_{56}} = \frac{1}{5 \hspace{.05cm} \Omega} + \frac{1}{2 \hspace{.05cm} \Omega} = \frac{2}{10 \hspace{.05cm} \Omega} + \frac{5}{10 \hspace{.05cm} \Omega} = \frac{7}{10 \hspace{.05cm} \Omega}$$

Po odwróceniu stronami dwóch powyższych równań, dostaniemy:

$$R_{12} = \tfrac{12}{7} \hspace{.05cm} \Omega \hspace{1cm} , \hspace{1cm} R_{56} = \tfrac{10}{7} \hspace{.05cm} \Omega$$

Po zastąpieniu oporników połączonych równolegle rezystorami R₁₂ i R₅₆, układ z początku zadania przedstawia się obecnie następująco:

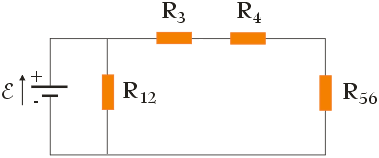
Zauważ, że rezystory R₃, R₄ oraz R₅₆ są połączone szeregowo, dlatego, aby jeszcze bardziej uprościć powyższy obwód obliczmy rezystancję zastępczą R₃₄₅₆ dla tej grupy rezystorów:

$$R_{3456} = R_3 + R_4 + R_{56} = 7 \hspace{.05cm} \Omega + 10 \hspace{.05cm} \Omega + \tfrac{10}{7} \hspace{.05cm} \Omega = 18 \hspace{.05cm} \tfrac{3}{7} \hspace{.05cm} \Omega$$

Ostatecznie, więc mamy obwód składający się z dwóch rezystorów połączonych równolegle:

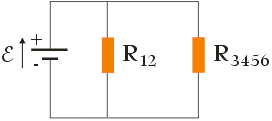
Pozostaje nam zatem obliczenie oporu zastępczego R_Z :

$$\frac{1}{R_Z} = \frac{1}{R_{12}} + \frac{1}{R_{3456}} = \frac{1}{\frac{12}{7} \hspace{.05cm} \Omega} + \frac{1}{\frac{129}{7} \hspace{.05cm} \Omega} = \frac{7}{12 \hspace{.05cm} \Omega} + \frac{7}{129\hspace{.05cm} \Omega} = \frac{987}{1548 \hspace{.05cm} \Omega}$$

$$R_Z = \frac{1548}{987} \hspace{.05cm} \Omega$$