Szeregowe i równoległe łączenie rezystorów

Rezystory podobnie jak cewki i kondensatory mogą być połączone na dwa główne sposoby. Jednym z tych sposobów jest połączenie szeregowe, drugim – połączenie równoległe. Poniżej znajdziesz opis i wyprowadzenie wzorów pozwalających obliczyć opór zastępczy układu rezystorów połączonych szeregowo oraz równolegle.

Szeregowe połączenie rezystorów

Gdy kilka oporników ustawionych jest jeden za drugim i połączonych przewodami tak, że różnica potencjałów U  przyłożona jest do jednego oraz drugiego końca takiego układu rezystorów to takie połączenie oporników nazywamy połączeniem szeregowym. Poniższy rysunek przedstawia prosty obwód elektryczny składający się z doskonałego źródła siły elektromotorycznej oraz rezystorów połączonych szeregowo, znajdujących się pomiędzy punktami A i B, między którymi źródło SEM utrzymuje stałą różnicę potencjałów ε.

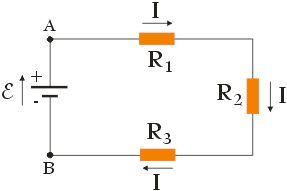
Zgodnie z powyższym rysunkiem nośniki ładunku mogą poruszać się w obwodzie tylko jedną drogą (brak węzłów w obwodzie), dlatego też przez każdy opornik musi przepływać prąd o takim samym natężeniu równym I.

Oporniki połączone szeregowo możemy zastąpić przez opornik zastępczy o oporze R_Z , przez który, przy tej samej różnicy potencjałów, przepłynie prąd o takim samym natężeniu, jak przez każdy z oporników stanowiących część układu oporników połączonych szeregowo. Na poniższym rysunku przedstawiono obwód elektryczny, w którym trzy oporniki z poprzedniego rysunku, zastąpiono jednym równoważnym (im) opornikiem o oporze R_Z .

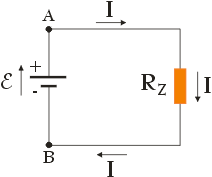
Aby wyprowadzić wyrażenie pozwalające obliczyć opór R_Z  opornika zastępczego (zastępującego oporniki połączone szeregowo) zastosujemy drugie prawo Kirchhoffa dla obydwu obwodów pokazanych na powyższych rysunkach. Zaczynając i kończąc analizę w punkcie A oraz poruszając się zgodnie z ruchem wskazówek zegara, dostaniemy dla pierwszego obwodu:

$$V_A \hspace{.1cm} – \hspace{.1cm} I \hspace{.05cm} R_1 \hspace{.1cm} – \hspace{.1cm} I \hspace{.05cm} R_2 \hspace{.1cm} – \hspace{.1cm} I \hspace{.05cm} R_3 + \varepsilon = V_A$$

z kolei dla obwodu z opornikiem zastępczym R_Z :

$$V_A \hspace{.1cm} – \hspace{.1cm} I \hspace{.05cm} R_Z + \varepsilon = V_A$$

Ponieważ natężenie prądu I  płynącego przez obydwa obwody przyjmuje jednakową wartość, dlatego też po przekształceniu powyższych wyrażeń względem prądu I  i przyrównaniu ich stronami, otrzymamy:

$$I = \frac{\varepsilon}{R_1 + R_2 + R_3} = \frac{\varepsilon}{R_Z} = I$$

Opór zastępczy rezystorów połączonych szeregowo – wzór

Widzimy więc, że wzór na opór zastępczy dla trzech rezystorów połączonych szeregowo ma postać:

$$R_Z = R_1 + R_2 + R_3$$

W ogólności, w przypadku n  rezystorów opór zastępczy możemy obliczyć stosując poniższe wyrażenie:

$$R_Z = \sum\limits_{i=1}^n R_i = R_1 + R_2 + … + R_n$$

gdzie R_i  to opór i-tego rezystora w obwodzie.

Równoległe połączenie rezystorów

Drugim sposobem łączenia rezystorów jest łączenie ich w sposób równoległy tj. taki, w którym oporniki z jednej oraz z drugiej strony połączone są za pomocą wspólnych przewodów, do końców których przykładana jest różnica potencjałów U. Takie połączenie oporników powoduje, że na każdym z nich występuje takie samo napięcie o wartości U, które wytwarza na każdym rezystorze prąd o różnym natężeniu (w przypadku rezystorów o jednakowym oporze, prąd przepływający przez te rezystory będzie miał oczywiście taką samą wartość). Zauważ, że zgodnie z poniższym rysunkiem prąd ze źródła SEM może poruszać się kilkoma drogami (prąd dopływając do węzła ulega rozgałęzieniu), co uzasadnia prawdziwość wcześniejszego stwierdzenia.

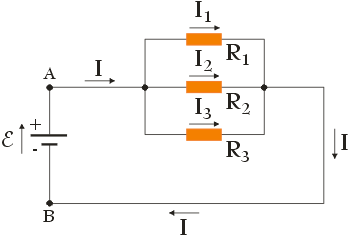
W związku z powyższym możemy zapisać, że:

Podobnie jak w przypadku rezystorów połączonych szeregowo, także i w przypadku układu oporników połączonych równolegle możemy zastąpić je za pomocą jednego równoważnego im opornika o oporze R_Z. Do końców tego opornika przykładana jest taka sama różnica potencjałów U, powodująca powstanie prądu o natężeniu I  równym sumie natężeń prądów wytworzonych we wszystkich opornikach połączonych równolegle.

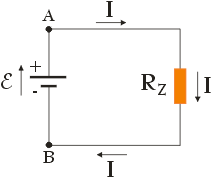
Aby wyprowadzić wzór pozwalający obliczyć opór zastępczy R_Z  oporników połączonych równolegle skorzystamy z pierwszego prawa Kirchhoffa. Zapisanie tego prawa dla układu oporników połączonych równoległe da nam:

$$I = I_1 + I_2 + I_3$$

Natężenie prądu I₁, I₂ oraz I₃ przepływającego, odpowiednio, przez opornik R₁, R₂  i R₃ obliczymy korzystając z definicji oporu elektrycznego. Ponieważ jak napisaliśmy wcześniej różnica potencjałów źródła SEM o wartości ε  przyłożona do układu oporników połączonych równolegle równa jest różnicy potencjałów na każdym z oporników z osobna, dlatego też:

$$I_1 = \frac{\varepsilon}{R_1} \hspace{1cm} , \hspace{1cm} I_2 = \frac{\varepsilon}{R_2} \hspace{1cm} , \hspace{1cm} I_3 = \frac{\varepsilon}{R_3}$$

Podstawiając każdy z prądów do równania I  = I₁  + I₂  + I₃, dostaniemy:

$$I = \frac{\varepsilon}{R_1} + \frac{\varepsilon}{R_2} + \frac{\varepsilon}{R_3} = \varepsilon \left( \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \right)$$

Podobne równanie otrzymamy dla obwodu z oporem zastępczym R_Z :

$$I = \frac{\varepsilon}{R_Z}$$

Porównując stronami dwa powyższe równania, uzyskamy:

$$I = \frac{\varepsilon}{R_1} + \frac{\varepsilon}{R_2} + \frac{\varepsilon}{R_3} = \varepsilon \left( \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \right) = \frac{\varepsilon}{R_Z} = I$$

Opór zastępczy rezystorów połączonych równolegle – wzór

Z powyższego wyrażenia wynika wzór pozwalający obliczyć opór zastępczy R_Z  dla trzech oporników połączonych równolegle:

$$\frac{1}{R_Z} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}$$

W ogólności, w przypadku n  rezystorów opór zastępczy możemy obliczyć stosując poniższe wyrażenie:

$$\frac{1}{R_Z} = \sum\limits^n_{i = 1} \frac{1}{R_i} = \frac{1}{R_1} + \frac{1}{R_2} + … + \frac{1}{R_n}$$