Prawa Kirchhoffa – zadanie nr 1

Obwód na poniższym rysunku składa się z rzeczywistego źródła siły elektromotorycznej SEM oraz rezystora o oporze R. Wiedząc, że różnica potencjałów na zaciskach źródła wynosi ε  = 12 V, opór wewnętrzny źródła r_w  = 2 Ω, a rezystancja opornika R  = 6 Ω, oblicz natężenie prądu przepływającego przez ten obwód.

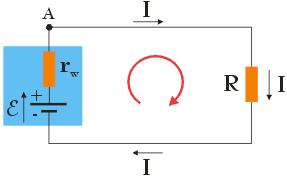
Wyrażenie pozwalające obliczyć natężenie prądu przepływającego przez obwód elektryczny można otrzymać korzystając z drugiego prawa Kirchhoffa. Analizę dla tego obwodu rozpoczniemy i zakończymy w punkcie A, zaznaczonym na powyższym rysunku, poruszając się zgodnie z ruchem wskazówek zegara, co symbolizuje czerwona strzałka (wybór punktu oraz kierunku analizy jest zupełnie dowolny – ważne jest, aby pamiętać o rozpoczęciu i zakończeniu analizy w tym samym punkcie tj. przeprowadzeniu analizy przy pełnym obejściu dowolnego oczka w obwodzie). Zwróć uwagę, że poruszając się zgodnie z ruchem wskazówek zegara, poruszamy się zgodnie z kierunkiem przepływu prądu w obwodzie, wyznaczonym przez strzałkę stojącą przy źródle SEM, która skierowana jest od bieguna o mniejszym potencjale (biegun -) do bieguna o większym potencjale (biegun +). Po przeprowadzeniu analizy dla punktu A, dostaniemy:

$$\hspace{.1cm} – \hspace{.1cm} I \hspace{.05cm} R + \varepsilon \hspace{.1cm} – \hspace{.1cm} I \hspace{.05cm} r_w = 0$$

gdzie:
I R  – spadek napięcia na rezystorze,
I r_w  – spadek napięcia na źródle SEM,
ε  – napięcie na zaciskach źródła SEM.

Przekształcając powyższe wyrażenie względem prądu I, dostaniemy:

$$I = \frac{\varepsilon}{R + r_w}$$

skąd po podstawieniu wartości liczbowych i wykonaniu obliczeń, otrzymamy szukaną wartość natężenia prądu równą:

$$I = \frac{12 \hspace{.05cm} \textrm{V}}{6 \hspace{.05cm} \Omega + 2 \hspace{.05cm} \Omega} = 1,\hspace{-.1cm}5 \hspace{.05cm} \textrm{A}$$

Aby pokazać, że wybór punktu i kierunku analizy obwodu nie ma wpływu na końcowy wynik, przeprowadźmy analizę dla punktu B, zaznaczonego na poniższym rysunku, poruszając się tym razem w kierunku przeciwnym do kierunku przepływu prądu, a więc przeciwnie do ruchu wskazówek zegara:

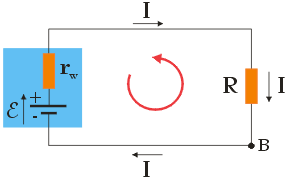
Z drugiego prawa Kirchhoffa dostaniemy wówczas:

$$I \hspace{.05cm} R + I \hspace{.05cm} r_w \hspace{.1cm} – \hspace{.1cm} \varepsilon = 0$$

Po przekształceniu powyższego równania względem I, podstawieniu wartości liczbowych oraz wykonaniu obliczeń, otrzymamy:

$$I = \frac{\varepsilon}{R + r_w} = \frac{12 \hspace{.05cm} \textrm{V}}{6 \hspace{.05cm} \Omega + 2 \hspace{.05cm} \Omega} = 1,\hspace{-.1cm}5 \hspace{.05cm} \textrm{A}$$

Przeprowadzając analizę dla punktu B dostaliśmy taką samą wartość natężenia prądu, co w przypadku analizy dla punktu A. Potwierdziliśmy tym samym, że wybór punktu oraz kierunku analizy nie ma wpływu na końcowy rezultat, w tym przypadku natężenia prądu.