Prawa Kirchhoffa – zadanie nr 2

Oblicz natężenie prądu płynącego przez amperomierz w obwodzie przedstawionym na poniższym rysunku wiedząc, że ε  = 1,5 V, R_w  = 1 Ω, R₁  = 2 Ω i R₂  = 4 Ω.

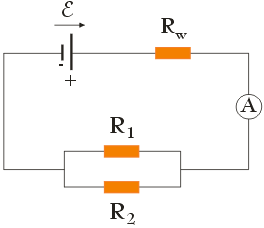
Zanim określimy kierunek przepływu prądu w obwodzie oraz zanim przeprowadzimy jego analizę, dokonajmy na początek jego uproszczenia. Rezystory R₁  i R₂  są połączone równolegle, w związku z czym możemy je zastąpić opornikiem zastępczym R₁₂. Opór tego rezystora obliczymy stosując poniższe wyrażenie:

$$\frac{1}{R_{12}} = \frac{1}{R_1} + \frac{1}{R_2} \hspace{1cm} \longrightarrow \hspace{1cm} \frac{1}{R_{12}} = \frac{R_1 + R_2}{R_1 \cdot R_2}$$

Po odwróceniu stronami powyższego równania, podstawieniu do niego wartości liczbowych podanych w treści zadania oraz wykonaniu obliczeń, dostaniemy:

$$R_{12} = \frac{R_1 \cdot R_2}{R_1 + R_2} = \frac{2 \hspace{.05cm} \Omega \cdot 4 \hspace{.05cm} \Omega}{2 \hspace{.05cm} \Omega + 4 \hspace{.05cm} \Omega} = 1,\hspace{-.1cm}33 \hspace{.05cm} \Omega$$

Zastępując rezystory R₁  i R₂  równoważnym im opornikiem R₁₂  spowodowaliśmy, że obecnie nasz obwód przedstawia się następująco:

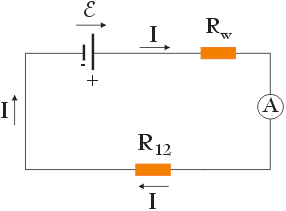
Kierunek przepływu prądu w obwodzie wyznaczony jest przez strzałkę stojącą przy źródle SEM tj. odbywa się zgodnie z ruchem wskazówek zegara. Ponadto, zgodnie z rysunkiem, prąd może płynąć przez obwód tylko jedną drogą (brak węzłów w obwodzie), zatem przez każdy element obwodu, a więc także i przez amperomierz, przepływa prąd o jednakowym natężeniu. Aby znaleźć wartość natężenia tego prądu skorzystamy z drugiego prawa Kirchhoffa. Stosując to prawo dla punktu A i poruszając się zgodnie z ruchem wskazówek zegara, dostaniemy:

$$\varepsilon \hspace{.1cm} – \hspace{.1cm} I \hspace{.05cm} R_w \hspace{.1cm} – \hspace{.1cm} I \hspace{.05cm} R_{12} = 0$$

Po przekształceniu powyższego wzoru względem I, dostaniemy:

$$I \left( R_w + R_{12} \right) = \varepsilon \hspace{1cm} \longrightarrow \hspace{1cm} I = \frac{\varepsilon}{R_w + R_{12}}$$

Wartość ε, R_w  i R₁₂  podano w treści zadania, zatem natężenie prądu I  przepływającego przez amperomierz wynosi:

$$I = \frac{1,\hspace{-.1cm}5 \hspace{.05cm} \textrm{V}}{1 \hspace{.05cm} \Omega + 1,\hspace{-.1cm}33 \hspace{.05cm} \Omega} = 0,\hspace{-.1cm}64 \hspace{.05cm} \textrm{A}$$