Prawa Kirchhoffa – zadanie nr 3

Oblicz natężenie prądu płynącego przez amperomierz w obwodzie przedstawionym na poniższym rysunku wiedząc, że ε  = 12 V, R_w  = 1 Ω, R₁  = 6 Ω i R₂  = 12 Ω.

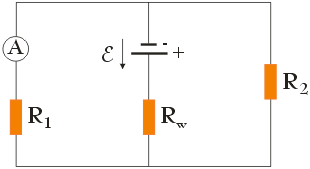
(Zadanie ze zbioru: K. Chyła Zbiór prostych zadań z fizyki dla uczniów szkół średnich)

Na początku przerysujmy powyższy obwód, wprowadzając na nim dodatkowe oznaczenia:

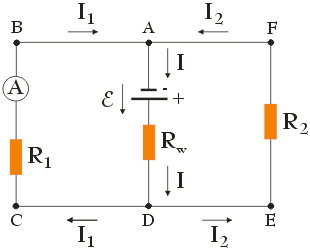
Zgodnie z rysunkiem, w obwodzie tym możemy wyróżnić dwa węzły – oznaczone literami A i D, trzy gałęzie łączące te węzły: lewą (ABCD), środkową (AD) i prawą (AFED) oraz trzy oczka: lewe (ABCDA), prawe (AFEDA) oraz oczko duże (ABCDEFA). Kierunek przepływu prądu w obwodzie wyznacza strzałka stojąca przy źródle SEM. Zauważ, że prąd I, wytwarzany przez źródło SEM, po dotarciu do węzła D rozgałęzia się na prądy I₁  oraz I₂. Prąd I₁  przepływa przez lewą gałąź, prąd I₂  – przez gałąź prawą. W każdej z tych gałęzi natężenie prądu nie ulega zmianie, zatem amperomierz w gałęzi lewej zmierzy prąd o natężeniu I₁. Aby znaleźć wartość tego prądu skorzystamy z drugiego prawa Kirchhoffa, zapisując je dla lewego oraz dużego oczka. Zaczynając i kończąc analizę w punkcie B oraz poruszając się zgodnie z ruchem wskazówek zegara, dostaniemy:

– dla lewego oczka:

$$\varepsilon \hspace{.1cm} – \hspace{.1cm} I \hspace{.05cm} R_w \hspace{.1cm} – \hspace{.1cm} I_1 \hspace{.05cm} R_1 = 0$$

– dla dużego oczka:

$$I_2 \hspace{.05cm} R_2 \hspace{.1cm} – \hspace{.1cm} I_1 \hspace{.05cm} R_1 = 0$$

Otrzymaliśmy dwa równania, w których występują aż trzy niewiadome: I, I₁  oraz I₂. Oznacza to, że potrzebujemy jeszcze jednego równania, które pozwoli nam powiązać te wszystkie prądy ze sobą. To „brakujące” równanie możemy otrzymać zapisując dla węzła D pierwsze prawo Kirchhoffa. Otrzymamy wówczas:

$$I = I_1 + I_2$$

Po przekształceniu powyższego równania względem prądu I₁, dostaniemy:

$$I_1 = I \hspace{.1cm} – \hspace{.1cm} I_2$$

Aby znaleźć wyrażenie na I  oraz I₂  przekształćmy dwa pierwsze równania:

$$\varepsilon \hspace{.1cm} – \hspace{.1cm} I \hspace{.05cm} R_w \hspace{.1cm} – \hspace{.1cm} I_1 \hspace{.05cm} R_1 = 0 \hspace{1cm} \longrightarrow \hspace{1cm} I = \frac{\varepsilon \hspace{.1cm} – \hspace{.1cm} I_1 \hspace{.05cm} R_1}{R_w}$$

oraz

$$I_2 \hspace{.05cm} R_2 \hspace{.1cm} – \hspace{.1cm} I_1 \hspace{.05cm} R_1 = 0 \hspace{1cm} \longrightarrow \hspace{1cm} I_2 = \frac{I_1 \hspace{.05cm} R_1}{R_2}$$

Podstawiając wzór na I  i I₂  do równania I₁  = I  – I₂, otrzymamy:

$$I_1 = \frac{\varepsilon \hspace{.1cm} – \hspace{.1cm} I_1 \hspace{.05cm} R_1}{R_w} \hspace{.1cm} – \hspace{.1cm} \frac{I_1 \hspace{.05cm} R_1}{R_2}$$

Mnożąc obydwie strony powyższego wyrażenia przez R_w  i R₂, dostaniemy:

$$I_1 \hspace{.05cm} R_2 \hspace{.05cm} R_w = \left( \varepsilon \hspace{.1cm} – \hspace{.1cm} I_1 \hspace{.05cm} R_1 \right) R_2 \hspace{.1cm} – \hspace{.1cm} I_1 \hspace{.05cm} R_1 \hspace{.05cm} R_w$$

skąd po przekształceniach uzyskamy ostateczne wyrażenie na I₁ :

$$I_1 = \frac{\varepsilon \hspace{.05cm} R_2}{R_1 \hspace{.05cm} R_w + R_2 \hspace{.05cm} R_w + R_1 \hspace{.05cm} R_2} = \frac{\varepsilon \hspace{.05cm} R_2}{R_w \left( R_1 + R_2 \right) + R_1 \hspace{.05cm} R_2}$$

Po podstawieniu wartości liczbowych podanych w treści zadania oraz wykonaniu obliczeń, otrzymamy szukaną wartość prądu I₁, równą:

$$I_1 = \frac{12 \hspace{.05cm} \textrm{V} \cdot 12 \hspace{.05cm} \Omega}{1 \hspace{.05cm} \Omega \cdot \left( 6 \hspace{.05cm} \Omega + 12 \hspace{.05cm} \Omega \right) + 6 \hspace{.05cm} \Omega \cdot 12 \hspace{.05cm} \Omega} = 1,\hspace{-.1cm}6 \hspace{.05cm} \textrm{A}$$