Prawa Kirchhoffa – zadanie nr 4

Oblicz natężenie prądu płynącego przez amperomierz w obwodzie przedstawionym na poniższym rysunku wiedząc, że ε  = 12 V, R_w  = 1 Ω i R  = 24 Ω.

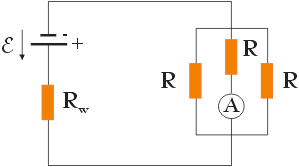
(Zadanie ze zbioru: K. Chyła Zbiór prostych zadań z fizyki dla uczniów szkół średnich)

Obwód przedstawiony na powyższym rysunku składa się z rzeczywistego źródła siły elektromotorycznej o oporze wewnętrznym R_w  oraz trzech oporników połączonych równolegle. Rezystory te mają jednakowy opór R  = 24 Ω, co oznacza, że przez każdy z tych oporników przepłynie prąd o takim samym natężeniu. Prąd ten, który oznaczymy jako I₁  równy jest 1/3 wartości całkowitego natężenia prądu I  przepływającego przez cały obwód:

$$I_1 = \tfrac{1}{3} \hspace{.05cm} I$$

Takie właśnie natężenie prądu zmierzy amperomierz umieszczony w środkowej gałęzi. Widzimy więc, że wielkością szukaną jest natężenie prądu I. Aby znaleźć wyrażenie na prąd I  zastąpmy na początku oporniki połączone równolegle rezystorem zastępczym R_Z. Każdy z tych trzech rezystorów, jak napisaliśmy wyżej, ma jednakowy opór, zatem:

$$\frac{1}{R_Z} = \frac{1}{R} + \frac{1}{R} + \frac{1}{R} = \frac{3}{R}$$

skąd po przekształceniu, otrzymamy:

$$R_Z = \tfrac{1}{3} \hspace{.05cm} R$$

Po zastąpieniu rezystorów opornikiem R_Z, obwód przedstawia się teraz następująco:

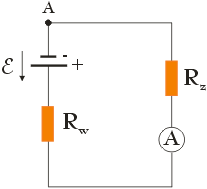
Kolejnym krokiem w znalezieniu wyrażenia na prąd I  jest skorzystanie z drugiego prawa Kirchhoffa. Zauważ, że zgodnie ze strzałką stojącą przy źródle SEM, kierunek przepływu prądu w obwodzie odbywa się przeciwnie do ruchu wskazówek zegara. Przeprowadzając analizę dla punktu A, zaznaczonego na powyższym rysunku, i poruszając się zgodnie z kierunkiem przepływu prądu otrzymamy:

$$\varepsilon \hspace{.1cm} – \hspace{.1cm} I \hspace{.05cm} R_w \hspace{.1cm} – \hspace{.1cm} I \hspace{.05cm} R_Z = 0$$

skąd po przekształceniu względem I, dostaniemy:

$$I = \frac{\varepsilon}{R_w + R_Z}$$

Wstawiając powyższe wyrażenie do wzoru na I₁, uzyskamy:

$$I_1 = \tfrac{1}{3} \hspace{.05cm} I = \frac{\varepsilon}{3 \left( R_w + R_Z \right)}$$

Ponieważ R_Z  = R /3, dlatego:

$$I_1 = \frac{\varepsilon}{3 \left( R_w + \tfrac{1}{3} \hspace{.05cm} R \right)} = \frac{\varepsilon}{3 \hspace{.05cm} R_w + R}$$

Po podstawieniu do powyższego równania wartości liczbowych podanych w treści zadania oraz wykonaniu obliczeń otrzymamy szukaną wartość natężenia prądu I₁, równą:

$$I_1 = \frac{12 \hspace{.05cm} \textrm{V}}{3 \hspace{.05cm} \Omega + 24 \hspace{.05cm} \Omega} = 0,\hspace{-.1cm}44 \hspace{.05cm} \textrm{A}$$