Prawa Kirchhoffa – zadanie nr 5

Oblicz natężenie prądu, jaki popłynie przez opór R  = 2 Ω, jeżeli siły elektromotoryczne ogniw i ich opory wewnętrzne są identyczne i wynoszą odpowiednio ε  = 1,5 V i R_w  = 0,5 Ω.

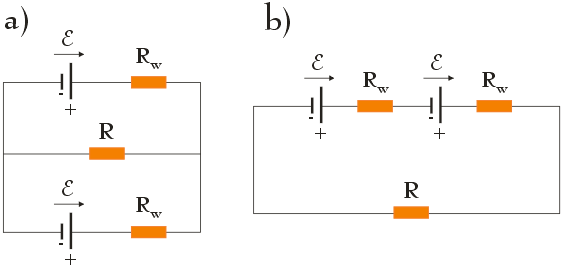
(Zadanie ze zbioru: K. Chyła Zbiór prostych zadań z fizyki dla uczniów szkół średnich)

Obwód elektryczny z podpunktu a) oraz b) składa się z dwóch rzeczywistych źródeł siły elektromotorycznej o oporze wewnętrznym R_w  oraz rezystora o oporze R. Różnica pomiędzy tymi obwodami tkwi w różnym sposobie połączenia źródeł SEM i opornika: w pierwszym przypadku mamy do czynienia z połączeniem równoległym, w drugim przypadku – z połączeniem szeregowym. Aby znaleźć natężenie prądu przepływającego przez rezystor R  skorzystamy z drugiego prawa Kirchhoffa.

Aby ułatwić zapisanie odpowiednich równań, na poniższych rysunkach zaznaczyliśmy kierunek przepływu prądu w obydwu obwodach:

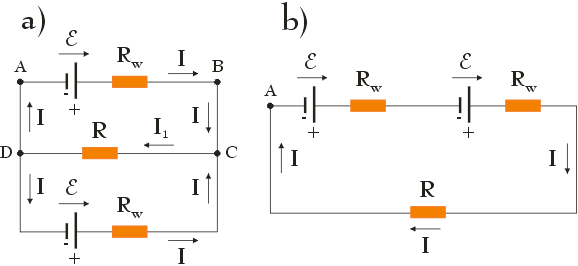
Obwód a)

Na początku zajmiemy się obwodem z podpunktu a). Analizę przeprowadzimy dla górnego oczka (ABCDA), poruszając się zgodnie z ruchem wskazówek zegara. Dostaniemy wówczas:

$$\varepsilon \hspace{.1cm} – \hspace{.1cm} I \hspace{.05cm} R_w \hspace{.1cm} – \hspace{.1cm} I_1 \hspace{.05cm} R = 0$$

skąd po przekształceniach otrzymamy wzór na prąd I₁  przepływający przez rezystor R :

$$I_1 = \frac{\varepsilon \hspace{.1cm} – \hspace{.1cm} I \hspace{.05cm} R_w}{R}$$

Następnie zapisując dla węzła C pierwsze prawo Kirchhoffa dostaniemy wyrażenie łączące prąd I₁  z prądem I. Zauważ, że do węzła C wpływają dwa prądy o natężeniu I, które „łączą się” w prąd I₁. Korzystając z tego faktu możemy więc zapisać:

$$I_1 = 2 \hspace{.05cm} I \hspace{1cm} \longrightarrow \hspace{1cm} I = \tfrac{1}{2} \hspace{.05cm} I_1$$

Po wstawieniu wyrażenia I  = I₁ /2 do równania I₁  = (ε  – I R_w )/R  oraz po podstawieniu wartości liczbowych i wykonaniu obliczeń, otrzymamy szukaną wartość natężenia prądu I₁, równą:

$$I_1 \hspace{.05cm} R = \varepsilon \hspace{.1cm} – \hspace{.1cm} \frac{I_1 \hspace{.05cm} R_w}{2} \hspace{1cm} \longrightarrow \hspace{1cm} I_1 = \frac{\varepsilon}{R + \tfrac{1}{2} \hspace{.05cm} R_w} = \frac{1,\hspace{-.1cm}5 \hspace{.05cm} \textrm{V}}{2 \hspace{.05cm} \Omega + \tfrac{1}{2} \cdot 0,\hspace{-.1cm}5 \hspace{.05cm} \Omega} = 0,\hspace{-.1cm}67 \hspace{.05cm} \textrm{A}$$

Obwód b)

Podobnie postąpimy z obwodem z podpunktu b). Wszystkie elementy wchodzące w skład tego obwodu, czyli dwa rzeczywiste źródła SEM i rezystor o oporze R, połączone są w sposób szeregowy, dlatego też przez cały ten obwód płynie prąd o jednakowym natężeniu. Zapisując drugie prawo Kirchhoffa dla punktu A, zaznaczonego na rysunku, dostaniemy:

$$\varepsilon \hspace{.1cm} – \hspace{.1cm} I \hspace{.05cm} R_w + \varepsilon \hspace{.1cm} – \hspace{.1cm} I \hspace{.05cm} R_w \hspace{.1cm} – \hspace{.1cm} I \hspace{.05cm} R = 0$$

Przekształcając powyższe równanie względem prądu I, podstawiając do niego wartości liczbowe oraz wykonując obliczenia, otrzymamy:

$$I = \frac{2 \hspace{.05cm} \varepsilon}{2 \hspace{.05cm} R_w + R} = \frac{2 \cdot 1,\hspace{-.1cm}5 \hspace{.05cm} \textrm{V}}{2 \cdot 0,\hspace{-.1cm}5 \hspace{.05cm} \Omega + 2 \hspace{.05cm} \Omega} = 1 \hspace{.05cm} \textrm{A}$$