Prawa Kirchhoffa – zadanie nr 6

Oblicz jakie napięcie wskaże woltomierz, jeżeli różnica potencjałów na zaciskach źródła SEM wynosi ε  = 100 V, a rezystancja oporników jest równa: R₁  = R₂  = 5 Ω, R₃  = 10 Ω, R₄  = 40 Ω.

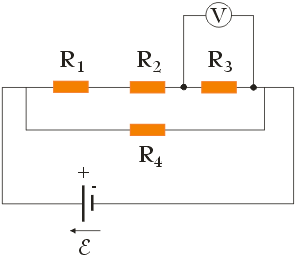
(Zadanie ze zbioru: K. Chyła Zbiór prostych zadań z fizyki dla uczniów szkół średnich)

Na początku zajmijmy się uproszczeniem obwodu pokazanego na powyższym rysunku. Zwróć uwagę, że rezystory R₁  i R₂  połączone są szeregowo, w związku z czym możemy je zastąpić opornikiem zastępczym R₁₂  o rezystancji równej (zobacz: Szeregowe i równoległe łączenie rezystorów):

$$R_{12} = R_1 + R_2 = 5 \hspace{.05cm} \Omega + 5 \hspace{.05cm} \Omega = 10 \hspace{.05cm} \Omega$$

Zastępując oporniki R₁  i R₂  rezystorem R₁₂  spowodowaliśmy, że obecnie nasz obwód elektryczny przedstawia się następująco:

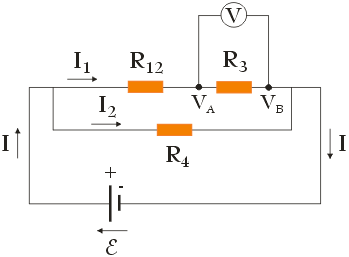
Aby znaleźć różnicę potencjałów U, jaką wskaże woltomierz przy przepływie prądu I₁  przez rezystor R₃  (zobacz: rysunek powyżej), skorzystamy z drugiego prawa Kirchhoffa. Prawo to zastosujemy dwukrotnie dla dużego oczka (czyli oczka składającego się ze źródła SEM oraz rezystorów R₁₂  i R₃ ): pierwszy raz, aby znaleźć wyrażenie na napięcie U  = V_A  – V_B , drugi raz – aby znaleźć wzór na natężenie prądu I₁.

Dla obydwu wspomnianych przypadków analizę rozpoczniemy w punkcie V_B , poruszając się zgodnie z kierunkiem przepływu prądu (czyli zgodnie z ruchem wskazówek zegara), przy czym przy wyznaczaniu różnicy potencjałów, zakończymy ją w punkcie V_A, a w przypadku drugim – w punkcie V_B  (tj. po obejściu całego oczka). W związku z powyższym dla pierwszego przypadku, dostaniemy:

$$V_B + \varepsilon \hspace{.1cm} – \hspace{.1cm} I_1 \hspace{.05cm} R_{12} = V_A$$

a dla drugiego:

$$\varepsilon \hspace{.1cm} – \hspace{.1cm} I_1 \hspace{.05cm} R_{12} \hspace{.1cm} – \hspace{.1cm} I_1 \hspace{.05cm} R_3 = 0$$

Z pierwszego równania otrzymamy wzór na U :

$$U = V_A \hspace{.1cm} – \hspace{.1cm} V_B = \varepsilon \hspace{.15cm} – \hspace{.05cm} I_1 \hspace{.05cm} R_{12}$$

a z drugiego wzór na I₁ :

$$I_1 = \frac{\varepsilon}{R_{12} + R_3}$$

Po wstawieniu wyrażenia na I₁  do wzoru na U, otrzymamy:

$$U = \varepsilon \hspace{.1cm} – \hspace{.1cm} \frac{\varepsilon \hspace{.05cm} R_{12}}{R_{12} + R_3} = \varepsilon \left( 1 \hspace{.1cm} – \hspace{.1cm} \frac{R_{12}}{R_{12} + R_3} \right)$$

i w konsekwencji szukaną wartość napięcia jaką zmierzy woltomierz, równą:

$$U = 100 \hspace{.05cm} \textrm{V} \cdot \left( 1 \hspace{.1cm} – \hspace{.1cm} \frac{10 \hspace{.05cm} \Omega}{10 \hspace{.05cm} \Omega + 10 \hspace{.05cm} \Omega} \right) = 50 \hspace{.05cm} \textrm{V}$$