Prawa Kirchhoffa – zadanie nr 7

Oblicz jakie napięcie wskaże woltomierz, jeżeli różnica potencjałów na zaciskach źródła SEM wynosi ε  = 100 V, a rezystancja oporników jest równa: R₁  = 5 Ω, R₂  = R₃  = 10 Ω.

(Zadanie ze zbioru: K. Chyła Zbiór prostych zadań z fizyki dla uczniów szkół średnich)

Sposób w jaki rozwiążemy to zadanie będzie podobny do tego jaki zastosowaliśmy w przypadku zadania Prawo Kirchhoffa – zadanie nr 6. Na początku korzystając z drugiego prawa Kirchhoffa zapiszmy dla oczka składającego się ze źródła SEM oraz rezystorów R₁  i R₃  wyrażenie na napięcie U  = V_A  – V_B . Analizę rozpoczniemy w punkcie V_B , a zakończymy w punkcie V_A, poruszając się zgodnie z kierunkiem przepływu prądu I  tj. zgodnie z ruchem wskazówek zegara (zobacz rysunek poniżej).

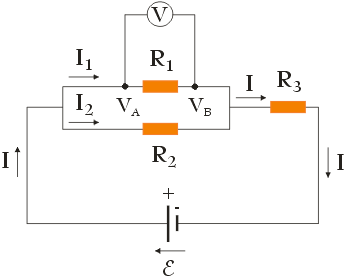
Dostaniemy:

$$V_B \hspace{.1cm} – \hspace{.1cm} I \hspace{.05cm} R_3 + \varepsilon = V_A \hspace{1cm} \longrightarrow \hspace{1cm} U = V_A \hspace{.1cm} – \hspace{.1cm} V_B = \varepsilon \hspace{.1cm} – \hspace{.1cm} I \hspace{.05cm} R_3$$

Wielkością szukaną jest, zgodnie z powyższym równaniem, natężenie prądu I, czyli prądu wytwarzanego przez źródło SEM. Aby dowiedzieć się ile wynosi to natężenie, uprościmy obwód pokazany na powyższym rysunku do tego stopnia, aby składał się on tylko z rezystora R_Z  – rezystora równoważnego opornikom R₁, R₂  i R₃. W tym celu najpierw obliczmy opór R₁₂  dla połączonych równolegle rezystorów R₁  i R₂ :

$$\frac{1}{R_{12}} = \frac{1}{R_1} + \frac{1}{R_2} = \frac{R_1 + R_2}{R_1 \cdot R_2} \hspace{1cm} \longrightarrow \hspace{1cm} R_{12} = \frac{R_1 \cdot R_2}{R_1 + R_2}$$

Teraz wyznaczmy opór R_Z. Zgodnie z poniższym rysunkiem:

rezystory R₁₂  i R₃  połączone są szeregowo, w związku z czym opór R_Z  wynosi:

$$R_Z = R_{12} + R_3 = \frac{R_1 \cdot R_2}{R_1 + R_2} + R_3 = \frac{R_1 \hspace{.05cm} R_2 + R_3 \left( R_1 + R_2 \right)}{R_1 + R_2}$$

Ostatecznie więc obwód z rezystorem R_Z  przedstawia się następująco:

Drugie prawo Kirchhoffa zapisane dla tego obwodu wynosi:

$$\varepsilon \hspace{.1cm} – \hspace{.1cm} I \hspace{.05cm} R_Z = 0 \hspace{1cm} \longrightarrow \hspace{1cm} I = \frac{\varepsilon}{R_Z}$$

Podstawiając powyższe równanie do wzoru na U, otrzymamy:

$$U = \varepsilon \hspace{.15cm} – \hspace{.05cm} I \hspace{.05cm} R_3 = \varepsilon \hspace{.15cm} – \hspace{.05cm} \frac{\varepsilon \hspace{.05cm} R_3}{R_Z} = \varepsilon \hspace{.1cm} – \hspace{.1cm} \frac{\varepsilon \hspace{.05cm} R_3 \left( R_1 + R_2 \right)}{R_1 \hspace{.05cm} R_2 + R_3 \left( R_1 + R_2 \right)} = \frac{\varepsilon \hspace{.05cm} R_1 \hspace{.05cm} R_2}{R_1 \hspace{.05cm} R_2 + R_3 \left( R_1 + R_2 \right)}$$

skąd po podstawieniu wartości liczbowych oraz wykonaniu obliczeń, dostaniemy wartość U  równą:

$$U = \frac{100 \hspace{.05cm} \textrm{V} \cdot 5 \hspace{.05cm} \Omega \cdot 10 \hspace{.05cm} \Omega}{5 \hspace{.05cm} \Omega \cdot 10 \hspace{.05cm} \Omega + 10 \hspace{.05cm} \Omega \cdot \left( 5 \hspace{.05cm} \Omega + 10 \hspace{.05cm} \Omega \right)} = 25 \hspace{.05cm} \textrm{V}$$