Szeregowe i równoległe łączenie rezystorów – zadanie nr 3

Oblicz opór zastępczy R_Z  układu oporników przedstawionych na poniższym rysunku wiedząc, że rezystancja oporników wynosi: R₁ = R₅ = 3 Ω, R₂ = 11 Ω, R₃ = R₆ = 2 Ω, R₄ = 6 Ω, R₇ = 5 Ω.

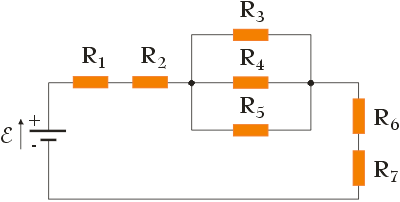
W przypadku obwodów elektrycznych składających się z dużej liczby rezystorów połączonych w sposób mieszany tj. równolegle oraz szeregowo (czyli tak jak na powyższym rysunku), dobrze jest, aby przy obliczaniu oporu zastępczego R_Z  oporników przyjąć odpowiednią strategię. Jedna z nich może polegać na obliczaniu składowych oporów zastępczych dla grup oporników połączonych w ten sam sposób (szeregowo lub równolegle), aby później pododawać otrzymane wartości uzyskując całkowity opór zastępczy R_Z . Inna, z kolei, na upraszczaniu (o ile jest to oczywiście możliwe) układu oporników do takiego stopnia, w którym wszystkie opory będą połączone w jednakowy sposób i wówczas, korzystając tylko z jednego wzoru na połączenie szeregowe albo równoległe, obliczać opór zastępczy R_Z . To jaką przyjmiemy strategię zależy oczywiście od nas oraz od konkretnego układu rezystorów.

Przed przystąpieniem do obliczenia oporu zastępczego R_Z  dla układu rezystorów musimy na podstawie sposobu ułożenia oporników w obwodzie określić sposób ich połączenia. Jeżeli rezystory z jednej oraz z drugiej strony połączone są za pomocą wspólnych przewodów, do końców których przykładana jest taka sama różnica potencjałów, czyli tak jak w przypadku rezystorów R₃, R₄ i R₅, wówczas rezystory te są połączone równolegle. Z kolei, gdy oporniki ustawione są jeden za drugim oraz połączone przewodnikami tak, że różnica potencjałów przyłożona jest do jednego oraz drugiego końca takiego układu rezystorów, czyli tak jak w przypadku rezystorów R₁ i R₂ oraz R₆ i R₇, wówczas rezystory te są połączone szeregowo. Takie różne ułożenie rezystorów w obwodzie powoduje, że przez oporniki połączone równolegle przepływa prąd o różnym natężeniu (poza przypadkiem, w którym oporniki mają jednakowy opór), a przez oporniki połączone szeregowo – prąd o jednakowym natężeniu. Na poniższym rysunku przedstawiono schematycznie przepływ prądu dla tego obwodu:

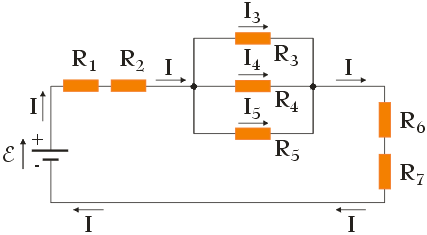
Aby uprościć nieco ten układ oporników zastąpmy rezystory R₃, R₄ i R₅ (połączone równolegle) opornikiem zastępczym o oporze R₃₄₅. W tym celu skorzystamy ze wzoru na opór zastępczy rezystorów połączonych równolegle:

$$\frac{1}{R_{345}} = \frac{1}{R_3} + \frac{1}{R_4} + \frac{1}{R_5}$$

Po podstawieniu w miejsce R₃, R₄ i R₅ wartości oporów podanych w treści zadania, dostaniemy:

$$\frac{1}{R_{345}} = \frac{1}{2 \hspace{.05cm} \Omega} + \frac{1}{6 \hspace{.05cm} \Omega} + \frac{1}{3 \hspace{.05cm} \Omega} = \frac{3}{6 \hspace{.05cm} \Omega} + \frac{1}{6 \hspace{.05cm} \Omega} + \frac{2}{6 \hspace{.05cm} \Omega} = \frac{6}{6 \hspace{.05cm} \Omega} = \frac{1}{\Omega}$$

skąd po odwróceniu powyższego równania (aby opór R₃₄₅ znalazł się w liczniku) otrzymamy wartość oporu R₃₄₅, równą:

$$R_{345} = 1 \hspace{.05cm} \Omega$$

Po zastąpieniu rezystorów R₃, R₄ i R₅ równoważnym im opornikiem R₃₄₅, spowodowaliśmy, że obecnie wszystkie oporniki połączone są w ten sam sposób tj. w sposób szeregowy:

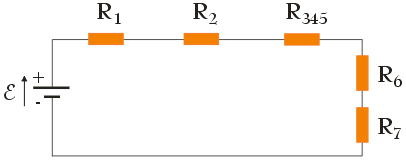
Aby więc obliczyć opór zastępczy R_Z  dla grupy rezystorów przedstawionej na powyższym rysunku skorzystamy ze wzoru na opór zastępczy rezystorów połączonych szeregowo:

$$R_Z = R_1 + R_2 + R_{345} + R_6 + R_7$$

Po podstawieniu do powyższego wzoru wartości liczbowych oraz wykonaniu obliczeń dostaniemy szukaną wartość oporu zastępczego R_Z , równą:

$$R_Z = 3 \hspace{.05cm} \Omega + 11 \hspace{.05cm} \Omega + 1 \hspace{.05cm} \Omega + 2 \hspace{.05cm} \Omega + 5 \hspace{.05cm} \Omega = 22 \hspace{.05cm} \Omega$$