Szeregowe i równoległe łączenie rezystorów – zadanie nr 2
Oblicz opór zastępczy RZ układu oporników przedstawionych na poniższym rysunku wiedząc, że rezystancja oporników wynosi: R1 = 4 Ω, R2 = 1 Ω, R3 = 7 Ω.
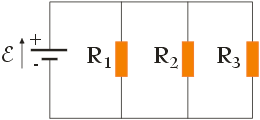
Rezystory R1, R2 i R3 połączone są z jednej oraz z drugiej strony za pomocą wspólnych przewodów, do końców których przykładana jest jednakowa różnica potencjałów ε. Oznacza to, że rezystory te są połączone równolegle, a więc aby obliczyć opór zastępczy RZ będziemy musieli skorzystać z poniższego wzoru:
$$\frac{1}{R_Z} = \sum\limits^n_{i = 1} \frac{1}{R_i} = \frac{1}{R_1} + \frac{1}{R_2} + … + \frac{1}{R_n}$$
Powyższy wzór dla układu trzech oporników przyjmie następującą postać:
$$\frac{1}{R_Z} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}$$
Po podstawieniu do powyższego wzoru wartości liczbowych oraz wykonaniu obliczeń, dostaniemy:
$$\frac{1}{R_Z} = \frac{1}{4 \hspace{.05cm} \Omega} + \frac{1}{1 \hspace{.05cm} \Omega} + \frac{1}{7 \hspace{.05cm} \Omega} = \frac{7}{28 \hspace{.05cm} \Omega} + \frac{28}{28 \hspace{.05cm} \Omega} + \frac{4}{28 \hspace{.05cm} \Omega} = \frac{39}{28} \hspace{.05cm} \frac{1}{\Omega}$$
Ponieważ wszystkie opory występują w mianowniku, dlatego też konieczne staje się odwrócenie lewej i prawej strony powyższego równania. Po wykonaniu takiego przekształcenia otrzymamy wartość oporu zastępczego RZ , równą:
$$R_Z = \tfrac{28}{39} \hspace{.05cm} \Omega$$
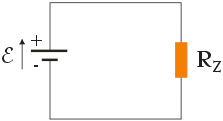
Na poniższym rysunku przedstawiono obwód z opornikiem o oporze RZ = 28/39 Ω, zastępującym oporniki R1, R2 i R3 połączone równolegle:

4 komentarze
Siema
Dodano dnia 29 października 2017 o godz. 09:26
Witam, jest mi ktoś w stanie wyjaśnić dlaczego przy dodawaniu wartości oporników 1/r1 itd. wychodzi na 7/28 ohma? jest to dla mnie kompletnie nie logiczne
Admin
Dodano dnia 29 października 2017 o godz. 10:29
Witam. Przy połączeniu równoległym opór rezystorów „wędruje” do mianownika. Aby obliczyć opór zastępczy Rz musimy wszystkie ułamki dodać do siebie. Aby to zrobić ułamki musimy „sprowadzić” do wspólnego mianownika – w przypadku tego zadania wspólnym mianownikiem ułamków jest 28 (mnożymy wszystkie mianowniki przez siebie i mamy: $4 \cdot 1 \cdot 7 = 28$). Znając wspólny mianownik, mamy: $\frac{1}{4} = \frac{7}{28}$ (bo $\frac{1}{4} \cdot \frac{1 \cdot 7}{4 \cdot 7} = \frac{7}{28}$), $\frac{1}{1} = \frac{28}{28}$ oraz $\frac{1}{7} = \frac{4}{28}$.
Dominik
Dodano dnia 30 listopada 2017 o godz. 22:37
wspólny mianownik , skoro mianownik powięszyłeś 7 razy to i góre powiększasz 7 razy. tak samo jest dalej w mianowniku masz 1 i w liczniku 1 to masz 28/28.
Dominik
Dodano dnia 30 listopada 2017 o godz. 22:38
nie zobaczyłem że już odpowiedział ktoś wyżej 😀