Prawa Keplera – zadanie nr 3

Pewien satelita poruszający się po orbicie wokół Ziemi znajduje się na wysokości 820 km nad jej powierzchnią, gdy jest najdalej od Ziemi, a na wysokości 480 km, gdy jest najbliżej Ziemi. Znajdź półoś wielką orbity a  oraz jej mimośród e. Promień Ziemi r_z  = 6370 km.

Aby znaleźć półoś wielką a  oraz mimośród e  orbity, po której satelita porusza się wokół Słońca, skorzystamy z poniższego rysunku:

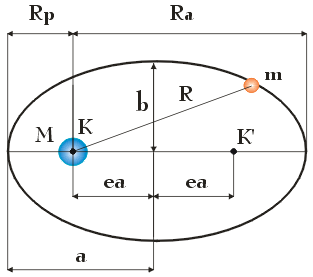
Najbliższa (peryhelium) oraz najdalsza (aphelium) odległość satelity od powierzchni Ziemi została oznaczona odpowiednio jako R_p  i R_a . Zauważ, że zgodnie z rysunkiem:

$$R_p + R_a = 2 \hspace{.05cm} a$$

w związku z czym:

$$a = \frac{R_p + R_a}{2} = \frac{6850 \hspace{.05cm} \textrm{km} + 7190 \hspace{.05cm} \textrm{km}}{2} = 7020 \hspace{.05cm} \textrm{km}$$

(do odległości podanych w treści zadania dodaliśmy promień Ziemi r_z )

Znając wartość półosi wielkiej orbity a  możemy przystąpić do obliczenia mimośrodu e  tej orbity. W tym celu ponownie skorzystamy z powyższego rysunku. Zwróć uwagę, że:

$$R_p + e \hspace{.05cm} a = a$$

Po przekształceniu powyższego wyrażenia względem e , podstawieniu wartości liczbowych oraz wykonaniu obliczeń, dostaniemy:

$$e = \frac{a \hspace{.1cm} – \hspace{.1cm} R_p}{a} = \frac{7020 \hspace{.05cm} \textrm{km} \hspace{.1cm} – \hspace{.1cm} 6850 \hspace{.05cm} \textrm{km}}{7020 \hspace{.05cm} \textrm{km}} = 0,\hspace{-.1cm}024$$

Uzyskana wartość mimośrodu e oznacza, że orbita po której satelita porusza się wokół Ziemi, ma kształt zbliżony do okręgu.