Potencjał elektryczny – zadanie nr 4

W dwóch wierzchołkach znajdującego się w próżni trójkąta równobocznego umieszczono ładunki + e  i – 2 e. Jaki ładunek należy umieścić w trzecim wierzchołku, aby potencjał pola elektrycznego w geometrycznym środku trójkąta wynosił zero?

Sytuację przedstawioną w treści zadania przedstawia poniższy rysunek:

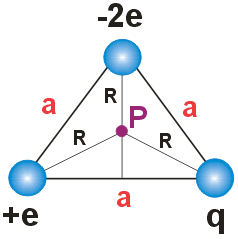
gdzie:
a – bok trójkąta,
R  – odległość od ładunku do środka geometrycznego P trójkąta równobocznego.

Wielkością szukaną jest wartość ładunku q, dla którego potencjał elektryczny w punkcie P jest równy V  = 0. Potencjał pola elektrycznego to wielkość skalarna wyrażona wzorem:

$$V = k \hspace{.05cm} \frac{q}{r}$$

gdzie:
k  – stała elektrostatyczna równa 9 ⋅ 10⁹ (N ⋅ m²)/C²,
q  – ładunek elektryczny,
r  – odległość od ładunku do punktu, w którym chcemy obliczyć potencjał pola elektrycznego.

W naszym przypadku odległość r  dla każdego z trzech ładunków przyjmuje jednakową wartość równą R  (środek geometryczny trójkąta równobocznego znajduje się w samym środku trójkąta, w związku z czym odległość od środka geometrycznego do każdego z ładunków jest taka sama), dlatego potencjał pola w punkcie P wynosi:

$$V = k \hspace{.05cm} \frac{e}{R} + k \hspace{.05cm} \frac{\hspace{.1cm} – \hspace{.1cm} 2 \hspace{.05cm} e}{R} + k \hspace{.05cm} \frac{q}{r} = 0$$

Po wyłączeniu przed nawias wspólnego czynnika k /R, dostaniemy:

$$\frac{k}{R} \left( e \hspace{.1cm} – \hspace{.1cm} 2 \hspace{.05cm} e + q \right) = 0$$

Wielkość k /R  jest różna od zera, dlatego potencjał pola V  = 0, gdy wyrażenie (e  – 2 e  + q ) = 0. Oznacza to, że ładunek q  musi być równy:

$$e \hspace{.1cm} – \hspace{.1cm} 2 \hspace{.05cm} e + q = 0 \hspace{1cm} \longrightarrow \hspace{1cm} q = 2 \hspace{.05cm} e \hspace{.1cm} – \hspace{.1cm} e = e$$