Natężenie pola elektrycznego – zadanie nr 6

Dla której z przedstawionych poniżej kombinacji jednakowych ładunków q  natężenie pola w środku kwadratu jest równe 0? Ile wynosi potencjał w środku poszczególnych kwadratów?

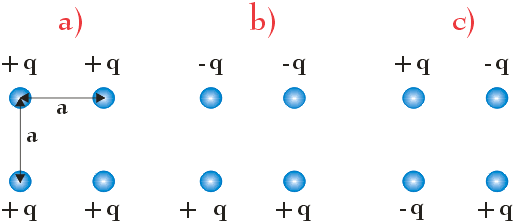
(Zadanie ze zbioru: K. Chyła Zbiór prostych zadań z fizyki dla uczniów szkół średnich)

Przypadek a)

Wszystkie ładunki są naładowane dodatnio, dlatego natężenie pola wytwarzanego przez każdy z tych ładunków jest skierowane od niego. Przedstawia to poniższy rysunek:

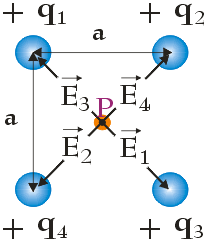
Dla czytelności początek każdego wektora umieściliśmy w punkcie, w którym obliczane jest wypadkowe natężenie pola, czyli w punkcie znajdującym się w środku okręgu oznaczonym jako P.

Wypadkowe natężenie pola $\vec{E}_{wyp}$  jest sumą wektorową wszystkich wektorów:

$$\vec{E}_{wyp} = \vec{E}_1 + \vec{E}_2 + \vec{E}_3 + \vec{E}_4$$

Zwróć uwagę, że wektory $\vec{E}_1$  i  $\vec{E}_3$  oraz  $\vec{E}_2$  i  $\vec{E}_4$ są względem siebie przeciwnie skierowane, a ponieważ ich długości są takie same (jednakowa wartość ładunku i odległości ładunku od środka okręgu), dlatego $\vec{E}_1$  = – $\vec{E}_3$  oraz  $\vec{E}_2$  = – $\vec{E}_4$.

Po podstawieniu tych relacji do wzoru na $\vec{E}_{wyp}$, otrzymamy:

$$\vec{E}_{wyp} = \hspace{.1cm} – \hspace{.1cm} \vec{E}_3 \hspace{.1cm} – \hspace{.1cm} \vec{E}_4 + \vec{E}_3 + \vec{E}_4 = 0$$

W podobny sposób obliczymy wypadkowy potencjał pola V_wyp . Potencjał V  wytwarzany przez każdy z tych ładunków w punkcie P wynosi:

$$V = k \hspace{.05cm} \frac{q}{\frac{\sqrt{2}}{2} \hspace{.05cm} a} = \frac{2 \hspace{.05cm} k \hspace{.05cm} q}{\sqrt{2} \hspace{.05cm} a}$$

gdzie $\frac{\sqrt{2}}{2} a$ to odległość dzieląca ładunek q  od punktu P, równa połowie długości przekątnej kwadratu o boku a.

Potencjał pola jest wielkością skalarną (nie posiadającą zwrotu), dlatego jego wypadkowa wartość w punkcie P jest sumą algebraiczną potencjałów pochodzących od każdego z ładunków. Ponieważ wszystkie ładunki są jednakowe, dlatego:

$$V_{wyp} = 4 \cdot \frac{2 \hspace{.05cm} k \hspace{.05cm} q}{\sqrt{2} \hspace{.05cm} a} = \frac{4 \cdot 2 \hspace{.05cm} q}{4 \hspace{.05cm} \pi \hspace{.05cm} \varepsilon_0 \hspace{.05cm} \sqrt{2} \hspace{.05cm} a} = \frac{2 \hspace{.05cm} q}{\pi \hspace{.05cm} \varepsilon_0 \hspace{.05cm} \sqrt{2} \hspace{.05cm} a} = \frac{\sqrt{2} \hspace{.05cm} q}{\pi \hspace{.05cm} \varepsilon_0 \hspace{.05cm} a}$$

Przypadek b)

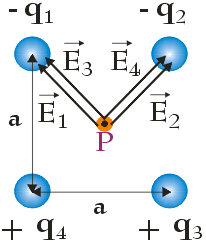
Wektory $\vec{E}_2$  i  $\vec{E}_4$ nachylone są do osi OX pod kątem φ  = 45^o (pod takim właśnie kątem nachylone są przekątne względem boków w kwadracie), z kolei wektory $\vec{E}_1$  i  $\vec{E}_3$ pod kątem α  = 135^o (90^o + 45^o). Aby obliczyć wypadkowe natężenie pola elektrostatycznego w punkcie P rozłożymy każdy z tych wektorów na dwie składowe: składową równoległą do osi OX oraz składową równoległą do osi OY (dla czytelności wszystkie składowe zostały rozsunięte – w rzeczywistości składowe E_1y , E_2y , E_3y  i E_4y nachodzą wzajemnie na siebie, podobnie jak składowe E_1x  i E_3x  oraz składowe E_2x  i E_4x ):

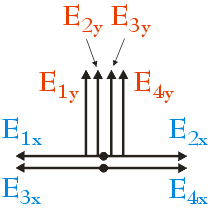
Składowe x  i y  mają taką samą wartość. Zauważ, że składowe E_2x  i E_4x  zwrócone są przeciwnie do składowych E_1x  i E_3x, dlatego też ich suma jest równa zero. Składowe y  wszystkich wektorów zwrócone są w tym samym kierunku i to właśnie ich suma da nam wypadkowe natężenie pola elektrostatycznego w punkcie P:

$$E_{wyp} = E_{1y} + E_{2y} + E_{3y} + E_{4y}$$

Wartość składowych E_2y  i E_4y wynosi:

$$E_{2y} = E_{4y} = k \hspace{.05cm} \frac{q}{\left( \frac{\sqrt{2}}{2} \hspace{.05cm} a \right)^2} \textrm{sin} \hspace{.05cm} 45^{\textrm{o}} = \frac{2 \hspace{.05cm} k \hspace{.05cm} q}{a^2} \cdot \frac{\sqrt{2}}{2} = \frac{\sqrt{2} \hspace{.05cm} k \hspace{.05cm} q}{a^2}$$

a składowych E_1y  i E_3y :

$$E_{1y} = E_{3y} = k \hspace{.05cm} \frac{q}{\left( \frac{\sqrt{2}}{2} \hspace{.05cm} a \right)^2} \textrm{sin} \hspace{.05cm} 135^{\textrm{o}} = \frac{2 \hspace{.05cm} k \hspace{.05cm} q}{a^2} \cdot \frac{\sqrt{2}}{2} = \frac{\sqrt{2} \hspace{.05cm} k \hspace{.05cm} q}{a^2}$$

Po obliczeniu sumy składowych x, dostaniemy:

$$E_{wyp} = 4 \cdot \frac{\sqrt{2} \hspace{.05cm} k \hspace{.05cm} q}{a^2} = 4 \cdot \frac{\sqrt{2} \hspace{.05cm} q}{4 \hspace{.05cm} \pi \hspace{.05cm} \varepsilon_0 \hspace{.05cm} a^2} = \frac{\sqrt{2} \hspace{.05cm} q}{\pi \hspace{.05cm} \varepsilon_0 \hspace{.05cm} a^2}$$

Wypadkowy potencjał dla tego układu ładunków jest z kolei równy:

$$V_{wyp} = \hspace{.1cm} – \hspace{.1cm} \frac{k \hspace{.05cm} q}{\left( \frac{\sqrt{2}}{2} \hspace{.05cm} a \right)} \hspace{.1cm} – \hspace{.1cm} \frac{k \hspace{.05cm} q}{\left( \frac{\sqrt{2}}{2} \hspace{.05cm} a \right)} + \frac{k \hspace{.05cm} q}{\left( \frac{\sqrt{2}}{2} \hspace{.05cm} a \right)} + \frac{k \hspace{.05cm} q}{\left( \frac{\sqrt{2}}{2} \hspace{.05cm} a \right)} = 0$$

Przypadek c)

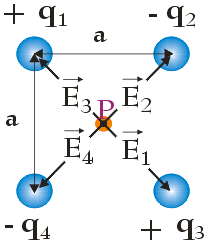
Dla tego układu ładunków mamy podobną sytuację co w przypadku a). Wektory $\vec{E}_2$  i  $\vec{E}_4$  oraz  $\vec{E}_1$  i  $\vec{E}_3$ zwrócone są w przeciwnym kierunku, dlatego wypadkowe natężenie pola wynosi:

$$\vec{E}_{wyp} = \vec{E}_1 + \vec{E}_2 + \vec{E}_3 + \vec{E}_4 = 0$$

Wypadkowy potencjał jest z kolei równy:

$$V_{wyp} = \frac{k \hspace{.05cm} q}{\left( \frac{\sqrt{2}}{2} \hspace{.05cm} a \right)} \hspace{.1cm} – \hspace{.1cm} \frac{k \hspace{.05cm} q}{\left( \frac{\sqrt{2}}{2} \hspace{.05cm} a \right)} + \frac{k \hspace{.05cm} q}{\left( \frac{\sqrt{2}}{2} \hspace{.05cm} a \right)} \hspace{.1cm} – \hspace{.1cm} \frac{k \hspace{.05cm} q}{\left( \frac{\sqrt{2}}{2} \hspace{.05cm} a \right)} = 0$$