Natężenie pola elektrycznego – zadanie nr 5

Oblicz natężenie i potencjał pola elektrostatycznego układu dwóch ładunków punktowych + q  i – q  odległych o l, w punkcie leżącym w połowie odległości pomiędzy nimi.

(Zadanie ze zbioru: K. Chyła Zbiór prostych zadań z fizyki dla uczniów szkół średnich)

Na początku przedstawmy sytuację opisaną w treści zadania za pomocą poniższego rysunku:

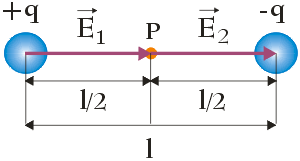
Ładunek + q  jest naładowany dodatnio, dlatego natężenie pola elektrostatycznego $\vec{E}_1$, związanego z tym ładunkiem, jest skierowane od niego. Ładunek – q  jest naładowany ujemnie i dlatego natężenie pola elektrostatycznego $\vec{E}_2$ zwrócone jest do niego. Aby wyznaczyć wypadkowe natężenie pola elektrostatycznego w punkcie P, położonym w połowie odległości pomiędzy ładunkami + q  i – q, musimy obliczyć sumę wektorową wektorów $\vec{E}_1$  i  $\rm \vec{E}_2$:

$$\vec{E}_{wyp} = \vec{E}_1 + \vec{E}_2$$

Natężenie pola wytwarzanego przez każdy z tych ładunków w punkcie P jest równe:

$$E_1 = k \hspace{.05cm} \frac{|q|}{\left( \frac{l}{2} \right)^2} = k \hspace{.05cm} \frac{q}{\left( \frac{l}{2} \right)^2}$$

oraz

$$E_2 = k \hspace{.05cm} \frac{|\hspace{.1cm} – \hspace{.1cm} q|}{\left( \frac{l}{2} \right)^2} = k \hspace{.05cm} \frac{q}{\left( \frac{l}{2} \right)^2}$$

Zauważ, że zgodnie z rysunkiem wektory $\vec{E}_{1}$  i  $\vec{E}_{2}$ mają jednakowe zwroty, dlatego aby obliczyć wypadkowe natężenie pola musimy dodać wartości tych wektorów opisane powyższymi wzorami (gdyby zwroty wektorów były przeciwne, obliczalibyśmy różnicę wartości wektorów). Po podstawieniu tych wyrażeń do wzoru na $\vec{E}_{wyp}$, otrzymamy:

$$E_{wyp} = k \hspace{.05cm} \frac{q}{\left( \frac{l}{2} \right)^2} + k \hspace{.05cm} \frac{q}{\left( \frac{l}{2} \right)^2} = 2 \hspace{.05cm} k \hspace{.05cm} \frac{q}{\left( \frac{l}{2} \right)^2} = 8 \hspace{.05cm} k \hspace{.05cm} \frac{q}{l^2}$$

Ponieważ $k = \dfrac{1}{4 \hspace{.05cm} \pi \hspace{.05cm} \epsilon_0}$, zatem:

$$E_{wyp} = \frac{8 \hspace{.05cm} q}{4 \hspace{.05cm} \pi \hspace{.05cm} \varepsilon_0 \hspace{.05cm} l^2} = \frac{2 \hspace{.05cm} q}{\pi \hspace{.05cm} \varepsilon_0 \hspace{.05cm} l^2}$$

W podobny sposób obliczymy wypadkowy potencjał pola V_wyp  w punkcie P. Zgodnie z definicją:

$$V = k \hspace{.05cm} \frac{q}{r}$$

dlatego:

$$V_1 = k \hspace{.05cm} \frac{q}{\left( \frac{l}{2} \right)} = \frac{2 \hspace{.05cm} k \hspace{.05cm} q}{l}$$

oraz

$$V_2 = k \hspace{.05cm} \frac{\hspace{.1cm} – \hspace{.1cm} q}{\left( \frac{l}{2} \right)} = \hspace{.1cm} – \hspace{.1cm} \frac{2 \hspace{.05cm} k \hspace{.05cm} q}{l}$$

Potencjał elektryczny jest wielkością skalarną, w związku z czym obliczenie jego wypadkowej wartości będzie polegało na algebraicznym (a nie wektorowym) dodaniu wartości potencjałów V₁  i V₂. Korzystając z tego faktu, dostaniemy:

$$V_{wyp} = V_1 + V_2 = \frac{2 \hspace{.05cm} k \hspace{.05cm} q}{l} \hspace{.1cm} – \hspace{.1cm} \frac{2 \hspace{.05cm} k \hspace{.05cm} q}{l} = 0$$