Arkusz maturalny z fizyki – poziom rozszerzony – rok 2018 („nowa matura”) – zadania nr 9 – 12

Wahadło wykonuje drgania, a więc siła reakcji napiętej liny $\vec{F_r}$  musi przyjmować większą wartość, niż siła grawitacji $\vec{F_g}$  (warunek kontynuacji drgań wahadła). W przypadku zaniku drgań, siły te będą się równoważyć.

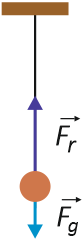
Prawidłowa odpowiedź: $\vec{F_r} \hspace{.05cm} > \hspace{.05cm} \vec{F_g}$.

Punktem wyjścia dla naszych obliczeń będzie wzór na okres T  wahadła matematycznego:

$$T = 2 \hspace{.05cm} \pi \hspace{.05cm} \sqrt{\dfrac{L}{g}}$$

gdzie L  to odległość dzieląca punkt zawieszenia wahadła od środka jego masy, a g  – przyspieszenie ziemskie.

Wahadło matematyczne to jeden z przykładów oscylatora harmonicznego, którego drgania zachodzą w płaszczyźnie pionowej, pod wpływem siły grawitacji. W większości zadań dotyczących wahadła matematycznego mamy do czynienia z ciałem o znikomo małej masie i rozmiarach, wskutek czego za długość wahadła przyjmujemy długość nici, na której ciało to jest zawieszone. W tym jednak przypadku nie możemy tego zrobić, gdyż kula zawieszona na linie ma średnicę równą 0,8 m. Oznacza to, że za długość L  wahadła musimy przyjąć długość l  liny oraz promień r  kuli (bierzemy pod uwagę odległość od punktu zawieszenia wahadła do środka masy kuli): $L = l + r$ .

Aby obliczyć czas t , po którym kula dotrze od najwyższego do najniższego punktu toru jej ruchu należy zauważyć, że czas ten odpowiada 1/4 okresu T  wahadła matematycznego (okres to czas, w jakim wykonywane jest jedno pełne drganie ciała), zatem:

$$t = \dfrac{T}{4} = \tfrac{1}{4} \cdot 2 \hspace{.05cm} \pi \hspace{.05cm} \sqrt{\dfrac{l + r}{g}} = \frac{\pi}{2} \hspace{.05cm} \sqrt{\dfrac{l + r}{g}}$$

Po podstawieniu do powyższego wyrażenia wartości liczbowych oraz wykonaniu obliczeń, dostaniemy:

$$t = \frac{3,\hspace{-.05cm}14}{2} \cdot \sqrt{\dfrac{6 \hspace{.05cm} \textrm{m} + 0,\hspace{-.05cm}4 \hspace{.05cm} \textrm{m}}{9,\hspace{-.05cm}81 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2}}} = 1,\hspace{-.05cm}27 \hspace{.05cm} \textrm{s} \approx 1,\hspace{-.05cm}3 \hspace{.05cm} \textrm{s}$$

Prawidłowa odpowiedź: czas potrzebny kuli na przebycie drogi od najwyższego do najniższego punktu jej toru wynosi ok. 1,3 s.

Rozbieżność wyników może wynikać z:

• pominięcia w modelu wahadła sił oporów ruchu
• rozmiarów kuli (model wahadła zakłada, że ciało zawieszone na linie/nici ma znikomo małą masę oraz rozmiary w stosunku do długości liny/nici)
• rozciągliwości liny (zgodnie z teorią lina nie powinna być rozciągliwa)
• dużych wychyleń kuli (wzór na okres wahadła matematycznego jest słuszny tylko dla drgań o małej amplitudzie)

Prawidłowa odpowiedź: jak napisano powyżej.

Opór zastępczy oporników w pomiarze nr 2 był równy 2 Ω. Rezystancja każdego opornika wynosi 4 Ω. Aby otrzymać wartość oporu z pomiaru 2 oporniki musiały być połączone w sposób równoległy. Jeden z takich układów oporników, dla którego opór zastępczy wynosi 2 Ω przedstawiono na poniższym rysunku:

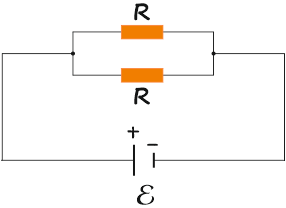
Dla pewności wykonajmy proste obliczenia:

$$\dfrac{1}{R_z} = \dfrac{1}{R} + \dfrac{1}{R} = \dfrac{1}{4 \hspace{.05cm} \Omega} + \dfrac{1}{4 \hspace{.05cm} \Omega} = \dfrac{1}{2 \hspace{.05cm} \Omega} \hspace{1cm} \longrightarrow \hspace{1cm} R_Z = 2 \hspace{.05cm} \Omega$$

Podpunkt a)

Podpunkt b)

Wykresem zależności U (R ) jest krzywa nazywaną hiperbolą. Zauważ, że dla coraz większych wartości rezystancji R  wartość napięcia U  będzie tylko nieznacznie rosnąć, zbliżając się, w tym przypadku, do U  = 6 V. I tyle właśnie powinna wynosić wartość SEM baterii.

Prawidłowa odpowiedź: wartość SEM baterii wynosi w przybliżeniu 6 V.

Rzeczywiste źródło siły elektromotorycznej (SEM), którego przykładem jest bateria, posiada pewien opór wewnętrzny r_w , na którego wartość składa się opór elektryczny wszystkich elementów wchodzących w skład danego źródła SEM. Aby obliczyć opór wewnętrzny oraz wartość źródła SEM skorzystamy z drugiego prawa Kirchhoffa zapisanego dla obwodu przedstawionego w zadaniu 10.1:

$$\varepsilon \hspace{.15cm} – \hspace{.1cm} I \hspace{.05cm} r_w \hspace{.15cm} – \hspace{.1cm} U = 0$$

gdzie ε  to wartość SEM baterii, I r_w  – spadek napięcia na baterii, związany z jej oporem wewnętrznym, a U  to wartość napięcia zmierzona woltomierzem, po dołączeniu do baterii układu oporników o oporze zastępczym R_z .

Aby ułatwić sobie obliczenia skorzystamy z prawa Ohma, które pozwoli nam wyeliminować natężenie prądu I  z powyższego równania (przez baterię oraz układ oporników, traktowany jako całość, przepływa prąd o tym samym natężeniu). Dostaniemy wówczas:

$$\varepsilon \hspace{.15cm} – \hspace{.1cm} \dfrac{U}{R_z} \hspace{.05cm} r_w \hspace{.15cm} – \hspace{.1cm} U = 0 \hspace{1cm} \longrightarrow \hspace{1cm} \varepsilon = \dfrac{U}{R_z} \hspace{.05cm} r_w + U$$

Mamy więc dwie niewiadome, których wartość musimy znaleźć. W tym celu zapiszmy dwa układy równań, do których wstawimy wartości liczbowe U  oraz R_z  dla 2-go oraz 3-go pomiaru (mamy tu pełną dowolność; tylko od nas zależy jakie dwa pomiary weźmiemy pod uwagę):

$$\varepsilon = \dfrac{3,\hspace{-.05cm}8 \hspace{.05cm} \textrm{V}}{2 \hspace{.05cm} \Omega} \hspace{.05cm} r_w + 3,\hspace{-.05cm}8 \hspace{.05cm} \textrm{V}$$

$$\varepsilon = \dfrac{4,\hspace{-.05cm}6 \hspace{.05cm} \textrm{V}}{4 \hspace{.05cm} \Omega} \hspace{.05cm} r_w + 4,\hspace{-.05cm}6 \hspace{.05cm} \textrm{V}$$

Gdy do pierwszego równania w miejsce ε  wstawimy drugie równanie, otrzymamy:

$$\dfrac{4,\hspace{-.05cm}6 \hspace{.05cm} \textrm{V}}{4 \hspace{.05cm} \Omega} \hspace{.05cm} r_w + 4,\hspace{-.05cm}6 \hspace{.05cm} \textrm{V} = \dfrac{3,\hspace{-.05cm}8 \hspace{.05cm} \textrm{V}}{2 \hspace{.05cm} \Omega} \hspace{.05cm} r_w + 3,\hspace{-.05cm}8 \hspace{.05cm} \textrm{V} \hspace{1cm} \longrightarrow \hspace{1cm} r_w \cdot \left( \dfrac{4,\hspace{-.05cm}6 \hspace{.05cm} \textrm{V}}{4 \hspace{.05cm} \Omega} \hspace{.15cm} – \hspace{.1cm} \dfrac{3,\hspace{-.05cm}8 \hspace{.05cm} \textrm{V}}{2 \hspace{.05cm} \Omega} \right) = \hspace{.15cm} – \hspace{.1cm} 0,\hspace{-.05cm}8 \hspace{.05cm} \textrm{V}$$

Po przekształceniu powyższego wyrażenia oraz wykonaniu obliczeń, dostaniemy:

$$r_w = \dfrac{\hspace{.15cm} – \hspace{.1cm} 0,\hspace{-.05cm}8 \hspace{.05cm} \textrm{V}}{\left( \dfrac{4,\hspace{-.05cm}6 \hspace{.05cm} \textrm{V}}{4 \hspace{.05cm} \Omega} \hspace{.15cm} – \hspace{.1cm} \dfrac{3,\hspace{-.05cm}8 \hspace{.05cm} \textrm{V}}{2 \hspace{.05cm} \Omega} \right)} = \dfrac{\hspace{.15cm} – \hspace{.1cm} 0,\hspace{-.05cm}8 \hspace{.05cm} \textrm{V}}{\hspace{.15cm} – \hspace{.1cm} \dfrac{6 \hspace{.05cm} \textrm{V} \cdot \Omega}{8 \hspace{.05cm} \Omega^2}} = 1,\hspace{-.05cm}1 \hspace{.05cm} \Omega$$

Znając wartość oporu wewnętrznego źródła możemy przystąpić do obliczenia jego wartości (korzystamy z pierwszego równania):

$$\varepsilon = \dfrac{3,\hspace{-.05cm}8 \hspace{.05cm} \textrm{V}}{2 \hspace{.05cm} \Omega} \cdot 1,\hspace{-.05cm}1 \hspace{.05cm} \Omega + 3,\hspace{-.05cm}8 \hspace{.05cm} \textrm{V} = 5,\hspace{-.05cm}9 \hspace{.05cm} \textrm{V}$$

Prawidłowa odpowiedź: ε  = 5,9 V, r_w  = 1,1 Ω.

Główna trudność tego zadania polega na odpowiednim narysowaniu normalnej do powierzchni, czyli prostej prostopadłej do powierzchni granicznej ośrodków w punkcie odbicia i załamania światła, względem której wyznaczamy położenie promienia odbitego oraz załamanego. Gdy uporamy się z tym problemem naszkicowanie promienia odbitego i załamanego będzie już formalnością. Aby tego dokonać skorzystamy z prawa odbicia oraz prawa załamania światła. Zgodnie z prawem odbicia kąt odbicia jest równy kątowi padania światła, w związku z czym kierunek promienia odbitego od powierzchni granicznej powietrze-szkło będzie wyznaczony przez kąt odbicia światła α. Aby narysować promień załamany należy zauważyć, że powietrze posiada mniejszy współczynnik załamania światła, niż szkło, w związku z czym kąt załamania światła β będzie mniejszy od kąta padania światła α (β  < α), a więc promień załamany będzie leżał blisko normalnej do powierzchni.

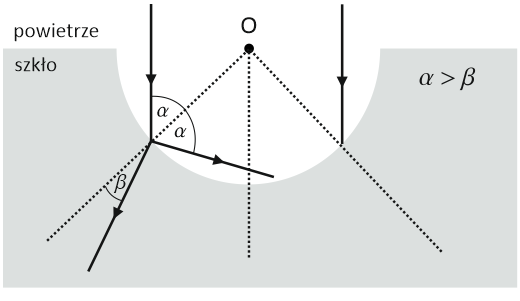
Zmiana kierunku rozchodzenia się światła przy przejściu przez dwa przezroczyste ośrodki (tzw. zjawisko załamania światła) występuje wtedy, gdy prędkość światła, po przejściu z jednego ośrodka do drugiego, ulega zmianie. Przedstawiony w zadaniu bieg promieni świetlnych będzie więc możliwy tylko wtedy, gdy światło w cieczy oraz w szkle będzie rozchodzić się z taką samą prędkością. Korzystając z prawa załamania światła, nazywanego również prawem Snella, możemy dodać, że w tym konkretnym przypadku kąt załamania światła w cieczy będzie równy kątowi padania światła na powierzchnię graniczną ciecz-szkło.

Prawidłowa odpowiedź: światło musi rozchodzić się z jednakową prędkością w obydwu ośrodkach.

Fala stojąca to fala powstająca wskutek interferencji (nakładania się) dwóch fal sinusoidalnych o takich samych długościach fali oraz amplitudach, poruszających się w przeciwnych kierunkach. Węzłami nazywamy miejsca, w których amplituda fali przyjmuje zerową wartość, a strzałki to miejsca, w których amplituda fali przyjmuje wartość największą. Wyobraźmy sobie falę stojącą jako nieco ‘zmodyfikowaną’ falę sinusoidalną. Każda połówka takiej sinusoidy ma długość równą połowie długości fali: λ /2. W ‘skład’ każdej takiej połówki wchodzą dwa węzły oraz jedna strzałka. Strzałka fali położona jest dokładnie w centralnej części takiej połówki, a więc jest ona oddalona od każdego z węzłów o wielkość równą połowie długości połówki sinusoidy tj. o wielkość λ /4.

Prawidłowa odpowiedź: odpowiedź A : λ /4.

Obydwa końce struny są unieruchomione, w związku z czym możemy je traktować jako węzły fali stojącej oddalone od siebie o wielkość l  równą długości tejże struny. Najprostszy schemat zakłada wytworzenie w tej strunie fali stojącej składającej się z dwóch węzłów oraz jednej strzałki, zlokalizowanej w środku struny (wyobraź sobie, że zostanie utworzona jedna z dwóch połówek fali – każda z tych połówek jest równa połowie długości fali). Wówczas długość struny będzie odpowiadać połowie długości fali λ:

$$l = \dfrac{\lambda}{2}$$

Gdy przekształcimy powyższy wzór względem λ  i dokonamy obliczeń, otrzymamy największą długość fali stojącej możliwej do wytworzenia w tej strunie:

$$\lambda_{max} = 2 \cdot l = 2 \cdot 90 \hspace{.05cm} \textrm{cm} = 180 \hspace{.05cm} \textrm{cm}$$

Prawidłowa odpowiedź: λ_max  = 180 cm.

Zacznijmy od zapisania ogólnego wzoru pozwalającego obliczać częstotliwości rezonansowe drgań wytworzonych w strunie o długości l  z unieruchomionymi końcami:

$$f_n = n \hspace{.05cm} \dfrac{V}{2 \hspace{.05cm} l}$$

gdzie n  to dodatnia liczba całkowita nazywana liczbą harmoniczną, a V  to prędkość fali wytworzonej w strunie.

Dla n  = 1 otrzymamy najniższą częstotliwość rezonansową w strunie nazywaną drganiem podstawowym albo pierwszą harmoniczną. Kolejne częstotliwości rezonansowe wytworzone w strunie są całkowitymi wielokrotnościami drgania podstawowego. W zadaniu podano dwie kolejne częstotliwości fal stojących równe 450 Hz oraz 675 Hz. Częstotliwość fali, której wartość wynosi 675 Hz oznaczmy jako f_n , a częstotliwość równą 450 Hz, jako f_n-1 . Dostaniemy wówczas:

$$f_n = n \hspace{.05cm} \dfrac{V}{2 \hspace{.05cm} l} = n \hspace{.05cm} f_1 \hspace{1cm} , \hspace{1cm} f_{n -1} = (n \hspace{.15cm} – \hspace{.1cm} 1) \hspace{.05cm} \dfrac{V}{2 \hspace{.05cm} l} = (n \hspace{.15cm} – \hspace{.1cm} 1) \hspace{.05cm} f_1$$

gdzie $f_1 = \tfrac{V}{2 \hspace{.05cm} l}$  to częstotliwość rezonansowa dla n  = 1 (drganie podstawowe).

Aby dowiedzieć się ile wynosi częstotliwość drgania podstawowego, podstawmy powyższe wyrażenia do wzoru $f_n \hspace{.1cm} – \hspace{.1cm} f_{n-1}$ :

$$f_n \hspace{.15cm} – \hspace{.1cm} f_{n-1} = n \hspace{.05cm} f_1 \hspace{.15cm} – \hspace{.1cm} (n \hspace{.15cm} – \hspace{.1cm} 1) \hspace{.05cm} f_1 = f_1$$

Zgodnie z powyższym wzorem częstotliwość drgania podstawowego w tej strunie wynosi:

$$ f_1 = 675 \hspace{.05cm} \textrm{Hz} \hspace{.15cm} – \hspace{.1cm} 450 \hspace{.05cm} \textrm{Hz} = 225 \hspace{.05cm} \textrm{Hz}$$

Znając częstotliwość drgania podstawowego możemy przystąpić do sprawdzenia czy możliwe jest wytworzenie w tej strunie fali stojącej o częstotliwości 1575 Hz. Jak napisaliśmy wyżej kolejne częstotliwości rezonansowe wytworzone w strunie są całkowitymi wielokrotnościami drgania podstawowego, zatem:

$$\dfrac{1575 \hspace{.1cm} \textrm{Hz}}{225 \hspace{.1cm} \textrm{Hz}} = 7$$

Wynikiem dzielenia jest liczba całkowita, a więc fala stojąca o częstotliwości 1575 Hz może zostać wytworzona w tej strunie.

Rozwiązania kolejnych zadań z tego arkusza maturalnego znajdziesz na poniższych stronach: