Arkusz maturalny z fizyki – poziom rozszerzony – rok 2018 („nowa matura”) – zadania nr 5 – 8

Układ pudełek znajduje się w spoczynku, w związku z czym wypadkowa sił działających na ten układ musi być równa zero. Pojawienie się siły tarcia statycznego F_Ts  działającej na górne pudełko, której wartość musimy znaleźć, związane jest bezpośrednio z siłą ciężkości F_g2  działającą na pudełko dolne. Siła ta przenoszona jest za pośrednictwem linki łączącej obydwa pudełka. Przyjmując do obliczeń wartość przyspieszenia grawitacyjnego g  = 10 m/s², mamy:

$$F_{Ts} = F_{g2} = m_2 \hspace{.05cm} g = 0,\hspace{-.05cm}2 \hspace{.05cm} \textrm{kg} \cdot 10 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2} = 2 \hspace{.05cm} \textrm{N}$$

gdzie m₂  to masa dolnego pudełka.

Prawidłowa odpowiedź: A – 3.

Aby obydwa pudełka zaczęły się poruszać, siła ciężkości działająca na dolne pudełko musi być większa od maksymalnej siły tarcia statycznego działającej na pudełko górne (zobacz: Tarcie. Siła tarcia):

$$\vec{F}_{g2} \hspace{.05cm} > \hspace{.05cm} \vec{F}_{Ts,max} \hspace{1cm} \longrightarrow \hspace{1cm} (m_2 + m_x) \hspace{.05cm} g \hspace{.05cm} > \hspace{.05cm} \mu_s \hspace{.05cm} N \hspace{1cm} \longrightarrow \hspace{1cm} (m_2 + m_x) \hspace{.05cm} g \hspace{.05cm} > \hspace{.05cm} \mu_s \hspace{.05cm} m_1 \hspace{.05cm} g$$

gdzie m₁  to masa górnego pudełka, a m_x  to masa piasku, jaką należy dosypać do dolnego pudełka, aby układ pudełek zaczął się poruszać.

Po skróceniu oraz przekształceniu stronami powyższego wyrażenia, otrzymamy:

$$m_x \hspace{.05cm} > \hspace{.05cm} \mu_s \hspace{.05cm} m_1 \hspace{.05cm} – \hspace{.05cm} m_2$$

i w konsekwencji:

$$m_x \hspace{.05cm} > \hspace{.05cm} 0,\hspace{-.05cm}25 \hspace{.05cm} \cdot 1 \hspace{.05cm} \textrm{kg} \hspace{.1cm} – \hspace{.05cm} 0,\hspace{-.05cm}2 \hspace{.05cm} \textrm{kg} \hspace{1cm} \longrightarrow \hspace{1cm} m_x \hspace{.05cm} > \hspace{.05cm} 0,\hspace{-.05cm}05 \hspace{.05cm} \textrm{kg}$$

Prawidłowa odpowiedź: masa piasku musi być większa niż 0,05 kg.

Praca W  wykonana przez siłę, z jaką pracownik działał na deskę, podczas ustawiania jej od pozycji poziomej do pozycji pionowej, odpowiada zmianie energii potencjalnej ΔE_p  deski. Wiemy, że deska jest sztywna oraz jednorodna, w związku z czym środek masy deski znajduje się w połowie jej długości, a więc w odległości 2 m od jej końców. Podczas podnoszenia środek masy deski przebywa w pionie drogę równą 2 m, zatem praca W  była równa:

$$W = \Delta \hspace{0.05cm} E_p = m \hspace{0.05cm} g \hspace{0.05cm} \Delta \hspace{0.02cm} h_{sm} = 20 \hspace{0.05cm} \textrm{kg} \cdot 10 \hspace{0.05cm} \tfrac{\textrm{m}}{\textrm{s}^2} \cdot 2 \hspace{0.05cm} \textrm{m} = 400 \hspace{0.05cm} \textrm{J}$$

Prawidłowa odpowiedź: praca jaką wykonał pracownik podczas podnoszenia deski była równa 400 J.

Podczas każdego z ‘postojów’ przy podnoszeniu deski, pracownik utrzymywał deskę nieruchomo, więc możemy założyć, że deska ta znajdowała się w równowadze statycznej. Aby obliczyć siłę, z jaką pracownik działał na linę, gdy deska była uniesiona względem podłoża pod kątem 25^o skorzystamy z warunku równowagi momentów sił działających na deskę:

Zgodnie z poniższym rysunkiem na deskę działają dwie siły: siła $\vec{F}$, z jaką pracownik działa na linę oraz siła ciężkości $\vec{F_g}$. Zwróć uwagę, że siły te działają w kierunku pionowym, a nas interesują składowe tych sił, prostopadłe do deski (deska jest nachylona pod kątem 25^o względem podłoża). Obliczenia przeprowadzimy dla momentów sił mierzonych względem punktu podparcia deski oznaczonego na rysunku literą P.

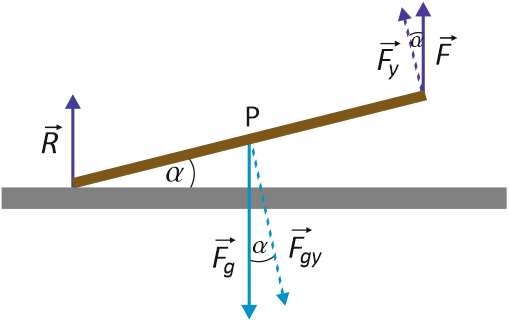
Z warunku równowagi momentów sił, mamy więc:

$$- \hspace{.05cm} \tfrac{l}{2} \hspace{.05cm} F_{gy} + l \hspace{.05cm} F_y = 0 \hspace{1cm} \longrightarrow \hspace{1cm} – \hspace{.05cm} \tfrac{l}{2} \hspace{.05cm} F_{g} \hspace{.08cm} \textrm{cos} \hspace{.05cm} \alpha + l \hspace{.05cm} F \hspace{.08cm} \textrm{cos} \hspace{.05cm} \alpha = 0$$

gdzie l /2 to ramię siły ciężkości (punkt zaczepienia siły ciężkości oddalony jest właśnie o taką odległość od punktu P), a l  to jednocześnie długość deski oraz ramię siły, z jaką pracownik działa na linę.

Po przekształceniu powyższego wzoru względem szukanej siły F , skróceniu wyrazów podobnych oraz podstawieniu wartości liczbowych i wykonaniu obliczeń, dostaniemy:

$$F = \dfrac{F_g}{2} = \dfrac{m \hspace{.05cm} g}{2} = \dfrac{20 \hspace{.05cm} \textrm{kg} \cdot 10 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2}}{2} = 100 \hspace{.05cm} \textrm{N}$$

Prawidłowa odpowiedź: siła, z jaką pracownik działał na linę była równa 100 N.

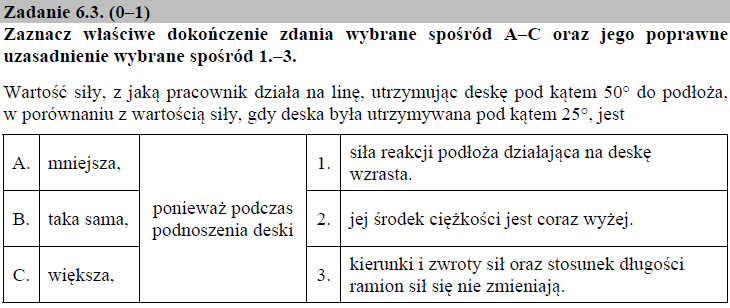
Zmiana kąta nachylenia deski względem podłoża nie wpływa na wartość siły, z jaką pracownik działa na linę. Zauważ, że gdybyśmy do wzoru opisującego równowagę momentów sił (patrz: zadanie 6.2) wstawili w miejsce kąta α inną wartość (np. β , gdzie β  ≠ α) to i tak wartości kątów uległyby skróceniu i otrzymalibyśmy dokładnie taki sam wzór na siłę F  jak w zadaniu 6.2. Dzieje się tak dlatego, że zarówno zwrot sił, jak i długość ich ramion nie ulegają zmianie podczas zmiany kąta nachylenia deski.

Prawidłowa odpowiedź: B – 3.

Zdanie 1

Zgodnie ze wzorem na pracę W , który zapisaliśmy w zadaniu 6.1, wartość tej pracy zależy tylko i wyłącznie od masy deski, przyspieszenia ziemskiego oraz drogi, jaką w pionie przebywa środek masy deski. Wielkości te nie zależą od miejsca zamocowania liny, a więc zdanie to jest prawdziwe.

Zdanie 2

Aby dowiedzieć się jak zmieni się wartość siły, z jaką pracownik działa na deskę, dokonajmy stosownych obliczeń. Ramię tej siły wynosi teraz 3/4 l , a więc korzystając ze wzoru opisującego równowagę momentów sił (zobacz: zadanie 6.2), mamy:

$$\tfrac{l}{2} \hspace{.05cm} F_{g} \hspace{.08cm} \textrm{cos} \hspace{.05cm} \alpha = \tfrac{3}{4} \hspace{.05cm} l \hspace{.05cm} F \hspace{.08cm} \textrm{cos} \hspace{.05cm} \alpha \hspace{1cm} \longrightarrow \hspace{1cm} F = \tfrac{2}{3} \hspace{.05cm} F_g = \tfrac{2}{3} \cdot 20 \hspace{.05cm} \textrm{kg} \cdot 10 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2} = 133,\hspace{-.05cm}3 \hspace{.05cm} \textrm{N}$$

Wartość tej siły jest większa od wartości uzyskanej w zadaniu 6.2, a więc zdanie to jest prawdziwe.

Zdanie 3

Gdybyśmy zapisali dla tego układu warunek równowagi sił, otrzymalibyśmy:

$$\vec{R} + \vec{F} = \vec{F_g}$$

gdzie $\vec{R}$  to siła reakcji podłoża.

Aby równanie to było spełnione siła reakcji podłoża musi ‘reagować’ na zmianę siły, z jaką pracownik działa na linę. Wraz ze wzrostem siły napięcia liny siła reakcji musi się zmniejszać i odwrotnie, dlatego też i to zdanie jest prawdziwe.

Prawidłowa odpowiedź: 1 – P , 2 – P , 3 – P.

Zdanie 1

Jak wynika z treści zadania układ składający się z chłopców oraz ich deskorolek możemy traktować jako układ izolowany tj. układ nie wymieniający masy z otoczeniem, w którym wypadkowa sił zewnętrznych działających na układ jest równa zero. Zgodnie z zasadą zachowania pędu całkowity pęd układu izolowanego pozostaje stały w czasie (zobacz: Zasada zachowania pędu), w związku z czym pęd układu chłopcy-deskorolki przyjmuje jednakową wartość przed oraz po ich odepchnięciu.

Zdanie 2

Masy chłopców oraz ich deskorolek są jednakowe, w związku z czym po odepchnięciu pęd układu deskorolka – chłopiec A będzie równy pędowi układu deskorolka – chłopiec B.

Zdanie 3

W pierwszym przypadku tj. gdy chłopiec A odepchnął się od ściany, siły wprawiające układ deskorolka – chłopiec A w ruch wykonały nad tym układem pracę, czego bezpośrednią konsekwencją jest zmiana energii kinetycznej tego układu. W drugim przypadku tj. gdy chłopiec A odepchnął się od deskorolki chłopca B praca wykonana przez siły wprawiające te dwa układy w ruch spowodowała zmianę energii kinetycznej zarówno chłopca A, jak i chłopca B. Ponieważ w jednym oraz w drugim przypadku została wykonana jednakowa praca, dlatego też możemy oczekiwać, że energia kinetyczna chłopca A (a więc także i jego prędkość) będzie mniejsza, niż w przypadku odepchnięcia się od ściany.

Prawidłowa odpowiedź: 1 – P, 2 – F, 3 – F.

Zacznijmy od zapisania ogólnej zależności zgodnie, z którą całkowita praca wykonana przez siły wprawiające w ruch układ deskorolka – chłopiec (W₁) przyjmuje jednakową wartość, co praca W₂ wykonana przez siły wprawiające w ruch układ deskorolki – chłopcy:

$$W_1 = W_2$$

Gdy chłopiec A odpycha się od ściany praca W₁ równa się zmianie jego energii kinetycznej E_k1A :

$$W_1 = \Delta \hspace{.02cm} E_{k1A} = \tfrac{1}{2} \hspace{.05cm}m_A \hspace{.05cm} V_{1A}^2 \hspace{.15cm} – \hspace{.1cm} \tfrac{1}{2} \hspace{.05cm}m_A \hspace{.05cm} V_{0,1A}^2 = \tfrac{1}{2} \hspace{.05cm}m_A \hspace{.05cm} V_{1A}^2$$

Początkowo chłopiec A nie poruszał się, dlatego też prędkość początkowa V_0,1A  = 0 m/s. Prędkość końcowa V_1A  jest znana i wynosi 4 m/s. W drugim przypadku tj. gdy chłopiec A odepchnął się od chłopca B praca W₂ równa się zmianie ich energii kinetycznych E_k2A  oraz E_k2B  (w poniższym wzorze pominięto wyrazy związane z początkową energią kinetyczną chłopców, gdyż ich prędkość początkowa była równa 0 m/s):

$$W_2 = \Delta \hspace{.02cm} E_{k2A} + \Delta \hspace{.02cm} E_{k2B} = \tfrac{1}{2} \hspace{.05cm}m_A \hspace{.05cm} V_{2A}^2 + \tfrac{1}{2} \hspace{.05cm}m_B \hspace{.05cm} V_{2B}^2$$

Podstawiając dwa powyższe wyrażenia do wzoru W₁ = W₂, dostaniemy:

$$ \tfrac{1}{2} \hspace{.05cm}m_A \hspace{.05cm} V_{1A}^2 = \tfrac{1}{2} \hspace{.05cm}m_A \hspace{.05cm} V_{2A}^2 + \tfrac{1}{2} \hspace{.05cm}m_B \hspace{.05cm} V_{2B}^2$$

Aby obliczyć prędkość V_2A , skorzystamy z zasady zachowania pędu dla tego układu:

$$\vec{p}_p = \vec{p}_k \hspace{1cm} \longrightarrow \hspace{1cm} 0 = \vec{p}_{2A} + \vec{p}_{2B} = m_A \hspace{.05cm} \vec{V}_{2A} + m_B \hspace{.05cm} \vec{V}_{2B}$$

gdzie $\vec{p}_p$ i $\vec{p}_k$ to odpowiednio początkowy i końcowy wektor pędu układu (chłopcy początkowo spoczywali, więc ich początkowy pęd wynosił 0).

Po przekształceniu powyższego wyrażenia, dostaniemy:

$$m_A \hspace{.05cm} \vec{V}_{2A} = \hspace{.15cm} – \hspace{.1cm} m_B \hspace{.05cm} \vec{V}_{2B}$$

Znak ‘-’ oznacza, że chłopcy po odepchnięciu się poruszali się w przeciwnych kierunkach. Zgodnie z treścią zadania masy chłopców i deskorolek są jednakowe, dlatego też m_A  = m_B . Korzystając z tego faktu możemy stwierdzić, że prędkości chłopców po ich odepchnięciu także muszą posiadać jednakową wartość: V_2A  = V_2B . Mamy więc:

$$ \tfrac{1}{2} \hspace{.05cm}m_A \hspace{.05cm} V_{1A}^2 = \tfrac{1}{2} \hspace{.05cm}m_A \hspace{.05cm} V_{2A}^2 + \tfrac{1}{2} \hspace{.05cm}m_A \hspace{.05cm} V_{2A}^2 = m_A \hspace{.05cm} V_{2A}^2$$

Po skróceniu, wykonaniu przekształceń oraz podstawieniu wartości liczbowych i wykonaniu obliczeń, otrzymamy:

$$V_{2A}^2 = \tfrac{1}{2} \hspace{.05cm} V_{1A}^2 \hspace{1cm} \longrightarrow \hspace{1cm} V_{2A} = \dfrac{V_{1A}}{\sqrt{2}} = \dfrac{4 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}}}{\sqrt{2}} = 2,\hspace{-.05cm}83 \tfrac{\textrm{m}}{\textrm{s}}$$

Prawidłowa odpowiedź: prędkość chłopca A po odepchnięciu się od deskorolki chłopca B wynosi 2,83 m/s.

Zdanie 1

Zgodnie z teorią całkowita praca wykonana przez gaz podczas przemian termodynamicznych równa się polu powierzchni zawartej wewnątrz wykresu w układzie p (V ) – w takim właśnie układzie został przedstawiony cykl termodynamiczny silnika I i II. Pole powierzchni zawartej wewnątrz wykresu dla obydwu silników cieplnych odpowiada polu prostokąta. Zwróć uwagę, że pole to w jednym oraz w drugim przypadku ‘obejmuje’ dwie kratki, w związku z czym całkowita praca wykonana przez gaz w silniku I oraz II musi przyjmować jednakową wartość.

Zdanie 2

Aby obliczyć maksymalną temperaturę gazu w silniku I oraz II skorzystamy z równania stanu gazu doskonałego nazywanego także równaniem Clapeyrona:

$$p \hspace{.05cm} V = n \hspace{.05cm} R \hspace{.05cm} T$$

gdzie: p , V  i T  to odpowiednio ciśnienie, objętość oraz temperatura gazu doskonałego, n  – liczba moli gazu doskonałego, a R  to tzw. uniwersalna stała gazowa.

Zgodnie z treścią zadania obydwa silniki zawierają jeden mol gazu doskonałego, dlatego n  = 1. Po przekształceniu powyższego wzoru względem temperatury T, dostaniemy:

$$T = \dfrac{p \hspace{.05cm} V}{R}$$

Po odczytaniu maksymalnych wartości ciśnienia i objętości (szukamy maksymalnej temperatury) dla jednego oraz drugiego silnika oraz po podstawieniu ich do powyższego wzoru i wykonaniu obliczeń, otrzymamy:

$$T_{1,max} = \dfrac{2 \hspace{.05cm} p_1 \cdot \hspace{.05cm} 3 \hspace{.05cm} V_1}{R} = \dfrac{6 \hspace{.1cm} p_1 \hspace{.05cm} V_1}{R}$$

oraz:

$$T_{2,max} = \dfrac{3 \hspace{.05cm} p_1 \cdot \hspace{.05cm} 2 \hspace{.05cm} V_1}{R} = \dfrac{6 \hspace{.1cm} p_1 \hspace{.05cm} V_1}{R}$$

Prawidłowa odpowiedź: 1 – taka sama, 2 – taka sama.

Zacznijmy od zapisania ogólnego wzoru opisującego sprawność η  dowolnego urządzenia:

$$\eta = \dfrac{E_{przek}}{E_{dost}}$$

gdzie E_przek  to energia przekształcana przez urządzenie, a E_dost  to energia dostarczona do urządzenia.

W przypadku silnika cieplnego powyższe wyrażenie możemy zapisać w następującej formie:

$$\eta = \dfrac{W}{Q_{pob}} = \dfrac{Q_{pob} \hspace{0.15cm} – \hspace{.1cm} Q_{od}}{Q_{pob}}$$

gdzie W  to praca wykonana przez silnik cieplny, a Q_pob  i Q_od  to odpowiednio ciepło pobrane oraz ciepło oddane przez silnik cieplny.

Wiemy, że silnik I pobiera 23 kJ ciepła (Q_pob ), a oddaje 19 kJ ciepła (Q_od ), w związku z czym, mamy:

$$\eta = \dfrac{Q_{pob} \hspace{0.15cm} – \hspace{.1cm} Q_{od}}{Q_{pob}} = \dfrac{23 \hspace{.05cm} \textrm{kJ} \hspace{.15cm} – \hspace{.1cm} 19 \hspace{.05cm} \textrm{kJ}}{23 \hspace{.05cm} \textrm{kJ}} = 0,\hspace{-.07cm}17$$

Sprawność urządzeń przyjęło się podawać w procentach, dlatego η  = 0,17 ⋅ 100% = 17%.

Prawidłowa odpowiedź: sprawność silnika I wynosi 17%.

Przemiana izochoryczna to proces termodynamiczny, podczas trwania którego objętość układu pozostaje stała (V  = constans). Wzór opisujący ciepło pobierane przez układ podczas tej przemiany przedstawia się następująco:

$$Q_V = n \hspace{.05cm} c_V \hspace{.05cm} \Delta \hspace{.02cm} T$$

gdzie n  to liczba moli gazu, c_V  – ciepło molowe gazu przy stałej objętości, a ΔT  to oczywiście zmiana temperatury gazu.

Z treści zadania wiemy, że w obydwu silnikach znajduje się jeden mol gazu doskonałego (n  = 1) o tym samym cieple molowym c_V . Aby obliczyć wartość ciepła Q_VII  pobranego przez silnik II musimy powiązać zmianę temperatury gazu z wielkością, która jest znana. Podczas przemiany izochorycznej zmiana temperatury gazu jest wprost proporcjonalna do zmiany jego ciśnienia, a wartość tą możemy odczytać dla obydwu silników z wykresów p (V ). Korzystając z równania stanu gazu doskonałego (patrz zadanie 8.1), mamy:

$$\Delta \hspace{.02cm} p \hspace{.05cm} V = n \hspace{.05cm} R \hspace{.05cm} \Delta \hspace{.02cm} T \hspace{1cm} \longrightarrow \hspace{1cm} \Delta \hspace{.02cm} T = \dfrac{\Delta \hspace{.02cm} p \hspace{.05cm} V}{n \hspace{.05cm} R} = \dfrac{\Delta \hspace{.02cm} p \hspace{.05cm} V}{R}$$

Po wprowadzeniu powyższego wzoru do równania opisującego ciepło przemiany izochorycznej silnika I oraz II oraz zauważeniu, że zmiana ciśnienia w silniku I wynosi p₁  (2 p₁  – p₁  = p₁ ), a w silniku II – 2 p₁  (3 p₁  – p₁  = 2 p₁ ), otrzymamy:

$$Q_{V\textrm{I}} = c_V \hspace{.05cm} \Delta \hspace{.02cm} T_{\textrm{I}} = \dfrac{c_V \hspace{.05cm} \Delta \hspace{.02cm} p_{\textrm{I}} \hspace{.05cm} V}{R} = \dfrac{p_1 \hspace{.05cm} c_V \hspace{.05cm} V}{R}$$

oraz:

$$Q_{V\textrm{II}} = c_V \hspace{.05cm} \Delta \hspace{.02cm} T_{\textrm{II}} = \dfrac{c_V \hspace{.05cm} \Delta \hspace{.02cm} p_{\textrm{II}} \hspace{.05cm} V}{R} = \dfrac{2 \hspace{.05cm} p_1 \hspace{.05cm} c_V \hspace{.05cm} V}{R} = 2 \hspace{.05cm} Q_{V\textrm{I}}$$

Ciepło Q_VI  jest znane i wynosi 3 kJ, w związku z czym ciepło Q_VII  wynosi 6 kJ.

Prawidłowa odpowiedź: ciepło pobierane przez silnik II podczas przemiany izochorycznej wynosi 6 kJ.

Rozwiązania kolejnych zadań z tego arkusza maturalnego znajdziesz na poniższych stronach: