Arkusz maturalny z fizyki – poziom rozszerzony – rok 2018 („nowa matura”) – zadania nr 1 – 4

Ruch pierwszego samochodu możemy podzielić na trzy etapy:

– etap pierwszy: ruch jednostajnie przyspieszony z przyspieszeniem a  > 0 – samochód ruszył z miejsca (V₀  = 0 m/s), by po czasie 2 s osiągnąć prędkość 10 m/s – wykresem tego ruchu jest linia oznaczona na poniższym wykresie rzymską cyfrą I,

– etap drugi: ruch jednostajny prostoliniowy – samochód przez 6 s poruszał się ze stałą prędkością V  = 10 m/s – wykresem tego ruchu jest linia oznaczona na poniższym wykresie rzymską cyfrą II,

– etap trzeci: ruch jednostajnie przyspieszony z przyspieszeniem a < 0 (tzw. ruch jednostajnie opóźniony) - wskutek hamowania (w czasie 2 s) samochód zmniejszył swoją prędkość z 10 m/s do 0 m/s - wykresem tego ruchu jest linia oznaczona na poniższym wykresie rzymską cyfrą III.

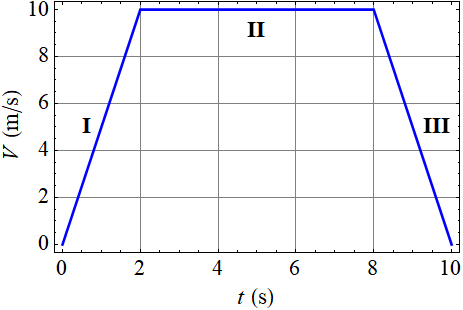
Całkowita droga przebyta przez pierwszy samochód

Całkowita droga s₁  przebyta przez pierwszy samochód jest równa polu powierzchni pod wykresem V (t ) (rysunek powyżej). Pole to odpowiada polu trapezu równoramiennego:

$$P = \dfrac{a + b}{2} \cdot h$$

gdzie a  i b  to odpowiednio dolna i górna i podstawa trapezu, h  – wysokość trapezu.

Zauważ, że w naszym przykładzie górna podstawa trapezu jest równa t₂  = 6 s (czas, w którym samochód poruszał się ruchem jednostajnym prostoliniowym), dolna podstawa wynosi t_c  = 10 s, gdzie t_c  to całkowity czas ruchu samochodu, z kolei wysokość trapezu jest równa h  = V_1,max  = 10 m/s (maksymalna prędkość tego samochodu). Po podstawieniu tych wartości do wzoru na pole trapezu, otrzymamy:

$$s_1 = P = \dfrac{t_c + t_2}{2} \cdot V_{1,max} = \dfrac{10 \hspace{.05cm} \textrm{s} + 6 \hspace{.05cm} \textrm{s}}{2} \cdot 10 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}} = 80 \hspace{.05cm} \textrm{m}$$

Maksymalna prędkość drugiego samochodu

Aby obliczyć maksymalną prędkość drugiego samochodu skorzystamy z faktu, że obydwa samochody przebyły taką samą drogę w tym samym czasie. Oznacza to, że droga s₂  drugiego samochodu przebyta w czasie t_c  = 10 s wyniosła 80 metrów. Wiemy także, że przez pierwszą połowę czasu trwania ruchu samochód ten zwiększał swoją prędkość poruszając się ruchem jednostajnie przyspieszonym, a przez drugą połowę ruchu – hamował ze stałym opóźnieniem. Podczas trwania każdej z tych faz ruchu samochód przebył drogę s  równą połowie całkowitej drogi s  = 1/2 s₂  tj. 40 metrów. Korzystając z powyższych informacji możemy stwierdzić, że maksymalną prędkość V_2,max  samochód ten osiągnął po czasie t  = 1/2 t_c  = 5 s (koniec pierwszej fazy ruchu, podczas której samochód się rozpędzał). Mamy więc:

$$V_{2,max} = a \hspace{.05cm} t$$

oraz

$$s = \dfrac{a \hspace{.05cm} t^2}{2} \hspace{1cm} \longrightarrow \hspace{1cm} a \hspace{.05cm} t = \dfrac{2 \hspace{.05cm} s}{t}$$

Po podstawieniu powyższego wyrażenia do wzoru na V_2,max , otrzymamy:

$$V_{2,max} = \dfrac{2 \hspace{.05cm} s}{t} = \dfrac{2 \cdot 40 \hspace{.05cm} \textrm{m}}{5 \hspace{.05cm} \textrm{s}} = 16 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}}$$

Prawidłowa odpowiedź: s₁ = 80 m, V_2,max = 16 m/s.

Podpunkt a)

Pole magnetyczne wytwarzane np. przez magnes podkowiasty przedstawia się graficznie przy pomocy tzw. linii pola magnetycznego reprezentujących linie wektora indukcji magnetycznej $\vec{B}$. Wektor ten jest styczny do tychże linii, w każdym ich punkcie, a ich rozmieszczenie obrazuje nam wielkość pola magnetycznego: im gęstsze rozmieszczenie linii pola, tym silniejsze pole magnetyczne.

Linie pola magnetycznego przechodzą przez magnes i tworzą zamknięte pętle. Koniec magnesu, z którego ‘wychodzą’ linie pola magnetycznego nazywamy północnym biegunem magnesu (N), a koniec magnesu do którego ‘wchodzą’ – południowym biegunem magnesu (S). Sytuację tą przedstawia poniższy rysunek.

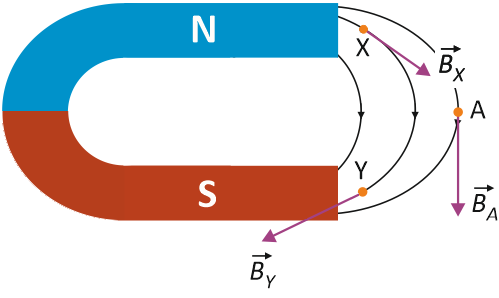
Zwróć uwagę, że zgodnie z tym co napisaliśmy wyżej wektor indukcji magnetycznej w punkcie X, Y oraz A jest styczny do linii pola magnetycznego (czarne krzywe).

Podpunkt b)

Zgodnie z definicją wartość natężenia pola elektrycznego E  wytwarzanego przez naładowaną cząstkę (w tym przypadku metalową kulkę) możemy obliczyć posługując się poniższym wzorem:

$$E = k \hspace{.05cm} \dfrac{q}{r^2}$$

gdzie:

k  – stała elektrostatyczna równa 9 ⋅ 10⁹ N ⋅ m²/C²,
q  – ładunek naładowanej cząstki,
r  – odległość pomiędzy środkiem cząstki, a punktem (leżącym na zewnątrz cząstki lub kulki), w którym chcemy obliczyć natężenie pola elektrycznego.

Zwróć uwagę, że punkty C i D znajdują się wewnątrz metalowej kulki w związku z czym natężenie pola elektrycznego w tych punktach wynosi 0. Aby obliczyć natężenie pola w punkcie B skorzystamy z faktu, że natężenie pola E_A  w punkcie A wynosi E  $\left(E_\textrm{A} = k \hspace{.05cm} \dfrac{q}{r_{\textrm{A}}^2} = E\right)$. Punkt A jest oddalony od środka kulki o wielkość r_A  równą trzem kratkom, z kolei punkt B o r_B  równą sześciu kratkom. Wiedząc, że r_B  = 2 r_A , mamy:

$$E_\textrm{B} = k \hspace{.05cm} \dfrac{q}{r_{\textrm{B}}^2} = k \hspace{.05cm} \dfrac{q}{\left(2 \hspace{.1cm} r_{\textrm{A}}\right)^2} = \dfrac{1}{4} \hspace{.05cm} k \hspace{.05cm} \dfrac{q}{r_{\textrm{A}}^2} = \dfrac{E}{4}$$

Prawidłowa odpowiedź: B = E /4, C = D = 0.

Zacznijmy od zapisania ogólnej zależności wiążącej przyspieszenie grawitacyjne a_G  dowolnej planety z jej masą M  oraz odległością r  od jej środka (zobacz: Grawitacja w pobliżu Ziemi):

$$a_G = \dfrac{G \hspace{.05cm} M}{r^2}$$

gdzie G  to stała grawitacji.

Zgodnie z powyższym wyrażeniem przyspieszenie grawitacyjne jest wprost proporcjonalne do masy M  planety oraz odwrotnie proporcjonalne do kwadratu odległości r. Aby dowiedzieć się jaka relacja występuje pomiędzy masami tych czterech planet wybierzmy pewną odległość r  spełniającą warunek r  > R₄  i odczytajmy wartość przyspieszenia grawitacyjnego dla tejże odległości dla każdej z tych planet. Zgodnie z wykresem, mamy:

$$a_{G2} \hspace{.05cm} (r) \hspace{.05cm} > \hspace{.05cm} a_{G1} \hspace{.05cm} (r) \hspace{.05cm} > \hspace{.05cm} a_{G3} \hspace{.05cm} (r) \hspace{.05cm} > \hspace{.05cm} a_{G4} \hspace{.05cm} (r) \hspace{1cm} \longrightarrow \hspace{1cm} \dfrac{G \hspace{.05cm} M_2}{r^2} > \dfrac{G \hspace{.05cm} M_1}{r^2} > \dfrac{G \hspace{.05cm} M_3}{r^2} > \dfrac{G \hspace{.05cm} M_4}{r^2}$$

i w konsekwencji:

$$M_2 \hspace{.05cm} > \hspace{.05cm} M_1 \hspace{.05cm} > \hspace{.05cm} M_3 \hspace{.05cm} > \hspace{.05cm} M_4$$

Prawidłowa odpowiedź: M₂  > M₁  > M₃  > M₄ .

Rozwiązania kolejnych zadań z tego arkusza maturalnego znajdziesz na poniższych stronach: