Arkusz maturalny z fizyki – poziom rozszerzony – rok 2018 („nowa matura”) – zadania nr 13 – 16

Zarówno cząstka α, jak i jądro złota są naładowane dodatnio, w związku z czym pomiędzy tymi jądrami będzie występowało oddziaływanie odpychające. Bezpośrednią konsekwencją tego oddziaływania będzie zakrzywianie toru ruchu cząstki α  – im mniejsza odległość cząstki α od jądra złota, tym większe zakrzywienie toru jej ruchu (większa siła oddziaływania odpychającego).

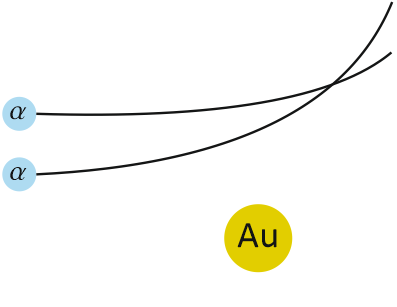
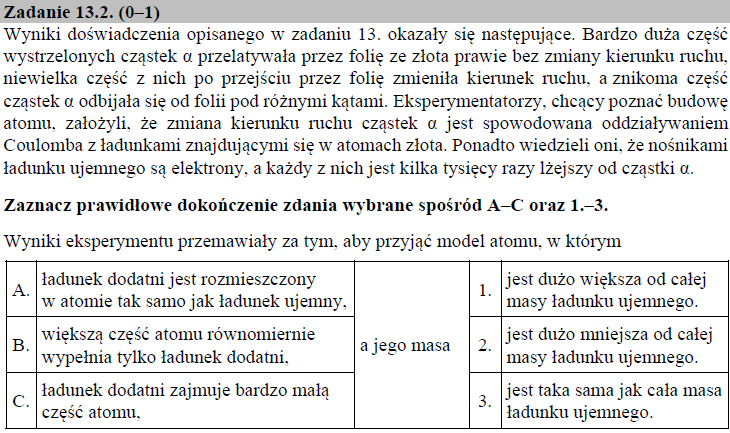
Wyniki eksperymentu sugerują, że:
– ładunek dodatni zajmuje bardzo małą część atomu, ponieważ bardzo duża część wystrzelonych cząstek α przelatywała przez folię bez zmiany kierunku ruchu,
– ładunek dodatni posiada o wiele większą masę, niż cały ładunek ujemny w atomie o czym świadczy fakt odbijania się niektórych cząstek α od folii złota.

Prawidłowa odpowiedź: C – 1.

Zdanie 1

Energia wiązania jądra atomowego określa pracę jaką należy wykonać, aby rozdzielić jądro atomowe na neutrony oraz protony. Wartość tej energii wzrasta wraz ze wzrostem liczby neutronów i protonów w jądrze atomowym, w związku z czym energia wiązania ciężkich jąder jest większa, niż jąder lekkich.

Zdanie 2

Masa jądra atomowego jest zawsze mniejsza od masy wszystkich neutronów i protonów (nazywanych ogólnie nukleonami) wchodzących w skład danego jądra atomowego. Ten ubytek masy, nazywany deficytem masy, związany jest z oddziaływaniami jądrowymi oraz energią potrzebną do utrzymania jądra atomowego w całości. Wartość tej energii jest tym większa, im większa jest liczba neutronów i protonów w jądrze. Oznacza to, że deficyt masy wzrasta wraz ze wzrostem liczby nukleonów, a zgodnie z odpowiedzią na zdanie nr 1, im większa liczba nukleonów, tym większa energia wiązania jądra atomowego.

Zdanie 3

Energia wiązania przypadająca na jeden nukleon przyjmuje różną wartość dla różnych jąder atomowych. Krzywa opisująca zależność energii wiązania przypadającej na jeden nukleon w funkcji liczby masowej początkowo rośnie (lekkie jądra), osiąga maksimum, po czym zaczyna stopniowo maleć (ciężkie jądra).

Prawidłowa odpowiedź: 1 – P , 2 – P , 3 – F.

Aby obliczyć początkową prędkość cząstki α skorzystamy z zasady zachowania energii. W analizie tej sytuacji pominiemy energię kinetyczną jądra złota, ponieważ wiemy, że jądro to pozostaje nieruchome, a więc jego prędkość i tym samym energia kinetyczna są równe zero. Interesuje nas zatem tylko energia kinetyczna cząstki α oraz potencjalna energia elektrostatyczna układu cząstka α – jądro złota:

$$E_{kp,\alpha} + E_{pp} = E_{kk,\alpha} + E_{pk}$$

gdzie $E_{kp,\alpha}$  i $E_{kk,\alpha}$  to odpowiednio początkowa oraz końcowa energia kinetyczna cząstki α, a $E_{pp}$  i $E_{pk}$  to odpowiednio początkowa oraz końcowa potencjalna energia elektrostatyczna układu cząstka α – jądro złota.

Poprzez termin końcowa  rozumiemy moment, w którym cząstka α znajduje się w najmniejszej możliwej odległości od jądra złota. Czas więc przystąpić do obliczenia początkowej energii kinetycznej cząstki α. Zgodnie z treścią zadania wiemy, że w chwili początkowej odległość dzieląca cząstkę α od jądra złota była bardzo duża, w związku z czym potencjalna energia elektrostatyczna tego układu jąder będzie bliska zeru i dlatego będziemy mogli ją pominąć. Dodatkowo, w chwili ‘spotkania się’ obydwu jąder, końcowa energia kinetyczna cząstki α będzie równa zeru, ponieważ oddziaływanie elektrostatyczne, mające charakter odpychający (cząstka α i jądro złota są dodatnio naładowane), będzie stopniowo zmniejszać prędkość cząstki α, aż do całkowitego wytracenia prędkości. Powyższe wyrażenie, po uwzględnieniu w/w uwag będzie więc wyglądać następująco:

$$E_{kp,\alpha} + 0 = 0 + E_{pk} \hspace{1cm} \longrightarrow \hspace{1cm} E_{kp,\alpha} = E_{pk} = \dfrac{k \hspace{.05cm} q_{\alpha} \hspace{.05cm} q_{\textrm{Au}}}{d}$$

Współczynnik k  wynosi 9 ⋅ 10⁹ N ⋅ m²/C², ładunek cząstki α jest równy q_α  = 2 q , ładunek jądra złota – q_Au  = 79 q  (q  to ładunek elementarny równy 1,6 ⋅ 10^-19 C), a d , czyli najmniejsza odległość na jaką cząstka α może zbliżyć się do jądra Au, wynosi 4 ⋅ 10^-14 m.

Po podstawieniu do powyższego wzoru wartości liczbowych oraz wykonaniu obliczeń, otrzymamy:

$$E_{kp,\alpha} = \dfrac{9 \cdot 10^9 \hspace{.05cm} \tfrac{\textrm{N} \cdot \textrm{m}^2}{\textrm{C}^2} \cdot 2 \cdot 79 \cdot \left( 1,\hspace{-.05cm}6 \cdot 10^{-19} \hspace{.05cm} \textrm{C} \right)^2}{4 \cdot 10^{-14} \hspace{.05cm} \textrm{m}} = 910 \cdot 10^{-15} \hspace{.05cm} \textrm{J} = 5,\hspace{-.05cm}7 \hspace{.05cm} \textrm{MeV}$$

(skorzystaliśmy z zależności: 1 eV = 1,6 ⋅ 10^-19 J)

Prawidłowa odpowiedź: początkowa energia kinetyczna cząstki α była równa 5,7 MeV.

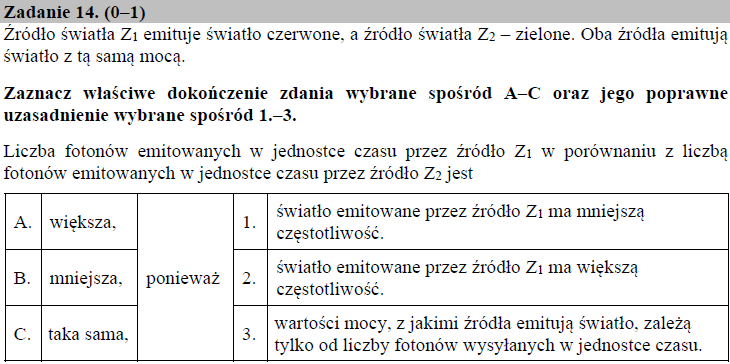
Moc każdego z tych źródeł światła możemy zapisać jako:

$$P = \dfrac{n \hspace{.05cm} E}{t} = \dfrac{n \hspace{.05cm} h \hspace{.05cm} f}{t}$$

gdzie n  to liczba fotonów, E  – energia pojedynczego fotonu równa h f , h  – stała Plancka, f  – częstotliwość światła, a t  – czas.

Po przekształceniu powyższego wzoru względem liczby fotonów n , dostaniemy:

$$n = \dfrac{P \hspace{.05cm} t}{h \hspace{.05cm} f}$$

Aby odpowiedzieć na pytanie postawione w niniejszym zadaniu obliczmy stosunek n₁ /n₂ , gdzie n₁  to liczba fotonów emitowanych przez źródło Z1, a n₂  – liczba fotonów emitowanych przez źródło Z2 (moc obydwu źródeł jest jednakowa, dlatego P₁  = P₂  = P ):

$$\dfrac{n_1}{n_2} = \dfrac{P \hspace{.05cm} t \cdot h \hspace{.05cm} f_2}{h \hspace{.05cm} f_1 \cdot P \hspace{.05cm} t} = \dfrac{f_2}{f_1}$$

Ponieważ częstotliwość światła czerwonego f₁  jest mniejsza od częstotliwości światła zielonego f₂  (f₁  < f₂ ), dlatego też stosunek liczby fotonów n₁ /n₂  > 1. Wynik ten oznacza, że źródło światła Z₁ emituje większą liczbę fotonów, niż źródło światła Z₂.

Prawidłowa odpowiedź: A – 1.

Zdanie 1

Zdanie to jest fałszywe, ponieważ z informacji do tego zadania wynika jedynie, że z taką właśnie prędkością (tj. 38,9 km/s) Merkury porusza się względem Słońca, gdy przechodzi przez aphelium. Dodatkowo, z drugiego prawa Keplera wynika, że planety poruszające się po orbitach wokół Słońca mają największe prędkości, gdy znajdują się w peryhelium, a więc najbliżej Słońca.

Zdanie 2

Im mniejsza odległość planety od Słońca, tym mniejsza orbita planety, a więc tym krótszy okres jej obiegu wokół Słońca. Merkury leży bliżej Słońca, aniżeli Ziemia, w związku z czym zdanie to jest oczywiście prawdziwe.

Zdanie 3

Zgodnie z informacją do tego zadania, podczas trwania tranzytu, Merkury, obserwowany z Ziemi, powoli przesuwał się na tle tarczy Słońca. Aby więc zjawisko tranzytu planety na tle tarczy Słońca mogło zostać zaobserwowane z powierzchni Ziemi, planeta ta musi znajdować się bliżej Słońca, aniżeli Ziemia. Z Ziemi możemy obserwować tylko przejście Merkurego i Wenus, a więc zdanie to jest fałszywe.

Prawidłowa odpowiedź: 1 – F , 2 – P , 3 – F.

Korzystamy z zasady zachowania energii, zgodnie z którą energia mechaniczna Merkurego w peryhelium jest równa jego energii mechanicznej w aphelium. W obydwu tych przypadkach energia mechaniczna Merkurego odpowiada sumie jego energii kinetycznej i grawitacyjnej energii potencjalnej układu Merkury – Słońce, w związku z czym:

$$E_{kp} + E_{pp} = E_{ka} + E_{pa}$$

gdzie $E_{kp}$  i $E_{ka}$  to energia kinetyczna Merkurego odpowiednio w peryhelium oraz aphelium, a $E_{pp}$  i $E_{pa}$  – grawitacyjna energia potencjalna układu Merkury – Słońce odpowiednio w peryhelium oraz aphelium.

Po podstawieniu do powyższego wzoru zależności na energię kinetyczną oraz grawitacyjną energię potencjalną, otrzymamy:

$$\dfrac{m \hspace{.05cm} V_p^2}{2} \hspace{.15cm} – \hspace{.1cm} \dfrac{G \hspace{.05cm} m \hspace{.05cm} M}{r_p} = \dfrac{m \hspace{.05cm} V_a^2}{2} \hspace{.15cm} – \hspace{.1cm} \dfrac{G \hspace{.05cm} m \hspace{.05cm} M}{r_a}$$

gdzie m  to masa Merkurego, V_p  – prędkość liniowa Merkurego w peryhelium, G  – stała grawitacji równa 6,67 ⋅ 10^-11 N ⋅ m²/kg², M  – masa Słońca, r_p  – peryhelium orbity Merkurego, V_a  – prędkość liniowa Merkurego w aphelium, a r_a  – aphelium orbity Merkurego.

Po skróceniu wyrazów podobnych oraz przekształceniu powyższego wyrażenia względem prędkości V_p , dostaniemy:

$$V_p^2 = V_a^2 + 2 \hspace{.05cm} G \hspace{.05cm} M \left( \dfrac{1}{r_p} \hspace{.15cm} – \hspace{.1cm} \dfrac{1}{r_a} \right) \hspace{1cm} \longrightarrow \hspace{1cm} V_p = \sqrt{V_a^2 + 2 \hspace{.05cm} G \hspace{.05cm} M \left( \dfrac{1}{r_p} \hspace{.15cm} – \hspace{.1cm} \dfrac{1}{r_a} \right)}$$

Prędkość Merkurego w aphelium jest znana i wynosi V_a  = 38,9 km/s, r_a  = 0,467 a.u. (a.u. to jednostka astronomiczna), r_p  = r_a  – 0,159 a.u. = 0,308 a.u., a masa Słońca M  jest równa w przybliżeniu 2 ⋅ 10³⁰ kg. Po podstawieniu tych danych do wzoru na V_p  oraz wykonaniu obliczeń, otrzymamy:

$$V_p = \sqrt{\left( 38,\hspace{-.05cm}9 \hspace{.05cm} \cdot 10^3 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}} \right)^2 + 2 \cdot 6,\hspace{-.05cm}67 \cdot 10^{-11} \hspace{.05cm} \tfrac{\textrm{N} \cdot \textrm{m}^2}{\textrm{kg}^2} \cdot 2 \cdot 10^{30} \hspace{.05cm} \textrm{kg} \cdot \left( \dfrac{1}{0,\hspace{-.05cm}308 \cdot 1,\hspace{-.05cm}5 \cdot 10^{11} \hspace{.05cm} \textrm{m}} \hspace{.15cm} – \hspace{.1cm} \dfrac{1}{0,\hspace{-.05cm}467 \cdot 1,\hspace{-.05cm}5 \cdot 10^{11} \hspace{.05cm} \textrm{m}} \right)} \approx 59 \hspace{.05cm} \tfrac{\textrm{km}}{\textrm{s}}$$

Prawidłowa odpowiedź: prędkość liniowa Merkurego w peryhelium wynosi ok. 59 km/s.

Zgodnie ze wzorem de Broglie’a długość fali materii λ  jest odwrotnie proporcjonalna do posiadanego przez nią pędu p :

$$\lambda = \dfrac{h}{p} = \dfrac{h}{m \hspace{.05cm} V}$$

gdzie h  to stała proporcjonalności nazywana stałą Plancka.

Widzimy, więc, że im większy pęd cząstek, tym krótsza długość fali materii (w naszym przypadku elektronów). Jeżeli układ dwóch równoległych, bardzo wąskich szczelin, przez które ‘przechodzą’ elektrony, potraktujemy jako siatkę dyfrakcyjną, wówczas będziemy mogli skorzystać z poniższego równania siatki dyfrakcyjnej:

$$d \hspace{.1cm} \textrm{sin} \hspace{.05cm} \theta = m \hspace{.05cm} \lambda$$

gdzie d  to stała siatki dyfrakcyjnej, θ  – kąt ugięcia światła na siatce dyfrakcyjnej, m  – rząd widma, a λ  – długość fali światła padającego na siatkę dyfrakcyjną.

Po przekształceniu powyższego wyrażenia względem kąta ugięcia światła, dostaniemy:

$$\textrm{sin} \hspace{.05cm} \theta = \dfrac{m \hspace{.05cm} \lambda}{d}$$

Zwróć uwagę, że im większa długość fali, tym większy kąt ugięcia fali na siatce dyfrakcyjnej, a więc tym większy ‘rozrzut’ prążków na ekranie. Zgodnie z powyższymi informacjami możemy jednoznacznie stwierdzić, że wiązka elektronów rozpędzona do większych prędkości utworzyła na ekranie obraz E_A (im większa prędkość, tym większy pęd elektronów; im większy pęd, tym mniejsza długość fali; im mniejsza długość fali, tym mniejszy kąt ugięcia fali na szczelinie, a więc tym mniejszy ‘rozrzut’ prążków na ekranie).

Prawidłowa odpowiedź: A – 4.

Rozwiązania kolejnych zadań z tego arkusza maturalnego znajdziesz na poniższych stronach: