Arkusz maturalny z fizyki – poziom rozszerzony – rok 2016 („nowa matura”) – zadania nr 5 – 8

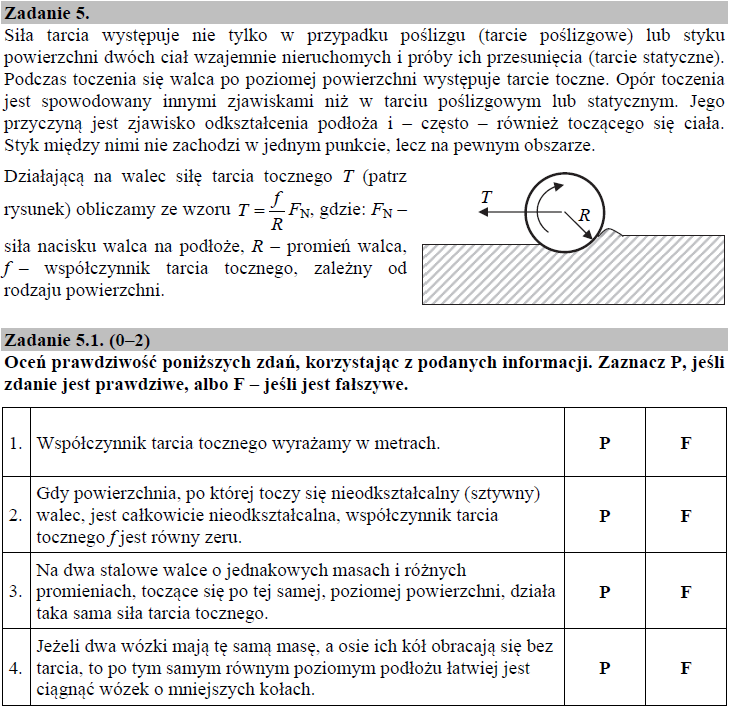
Zdanie 1

Dokonajmy rachunku jednostek:

$$\textrm{N} = \frac{x}{\textrm{m}} \cdot \textrm{N} = x \cdot \frac{\textrm{N}}{\textrm{m}}$$

Jednostka współczynnika tarcia tocznego, oznaczona jako x, musi mieć wymiar metra (m), bo tylko wtedy rachunek jednostek zostanie spełniony.

Zdanie 2

Zgodnie z treścią zadania przyczyną występowania tarcia tocznego jest zjawisko odkształcania się podłoża oraz toczącego się ciała. W przypadku, gdy sztywny (nieodkształcalny) walec będzie poruszał się po nieodkształcalnym podłożu, siła tarcia tocznego będzie równa zero, bo f  = 0 m.

Zdanie 3

Siła tarcia tocznego zależy wprost proporcjonalnie od współczynnika tarcia tocznego f  i siły nacisku F_n  oraz odwrotnie proporcjonalnie od promienia R  toczącego się ciała. Dwa stalowe walce, toczące się po tym samym podłożu, mają jednakowe masy oraz różne promienie. Oznacza to, że siła tarcia tocznego T  przyjmuje różną wartość dla każdego z walców.

Zdanie 4

Siła tarcia tocznego jest odwrotnie proporcjonalna do promienia R  toczącego się ciała: im większe koło wózka (większy promień koła), tym wartość tarcia tocznego jest mniejsza. Zgodnie z tym faktem, trudniej, a nie łatwiej, jest ciągnąć wózek o mniejszych kołach.

Prawidłowa odpowiedź: 1 – P,  2 – P,  3 – F,  4 – F.

Dwa stalowe walce mają jednakowe masy, długości oraz różne promienie. Siła tarcia tocznego jest odwrotnie proporcjonalna do długości promienia, w związku z czym na większy walec będzie oddziaływać mniejsza siła tarcia tocznego. A co z głębokością odkształcenia podłoża? Siła nacisku na podłoże ze strony małego i dużego walca jest taka sama. Wiemy jednak, że styk pomiędzy ciałem a podłożem nie zachodzi w jednym punkcie, lecz na pewnym obszarze. Im większa kula (większy promień), tym większa powierzchnia styku z podłożem. Związek pomiędzy siłą nacisku a powierzchnią styku opisuje dobrze znany wzór na ciśnienie:  $p = \frac{F}{S}$.  Zgodnie z tym wzorem, ciśnienie wywierane przez większy walec jest mniejsze, niż w przypadku mniejszego walca, dlatego spodziewamy się, że głębokość odkształcenia podłoża jest większa w przypadku walca o mniejszym promieniu.

Prawidłowa odpowiedź: C – 1.

Obydwa obrazy przedstawiają ten sam fragment sfery niebieskiej podczas dwóch nocy: 6 stycznia 2010 roku i 14 lutego 2010 roku. Planety, w przeciwieństwie do gwiazd, zmieniają swoje położenie na niebie. Spośród obiektów zaznaczonych na obrazach, tylko obiekt A zmienił swoje położenie, w związku z czym:

Prawidłowa odpowiedź: obiekt A jest planetą.

Paralaksa to zjawisko zmiany położenia bliższego obiektu na nieboskłonie względem obiektów bardziej odległych, spowodowane zmianą miejsca obserwacji wskutek przemieszczenia się (zmiany pozycji) obserwatora. W astronomii pomiar kąta paralaksy pozwala wyznaczyć odległość do danego ciała niebieskiego.

Prawidłowa odpowiedź: 1 – F,  2 – P,  3 – F.

Układ możemy potraktować jak wahadło matematyczne, w związku z czym okres drgań układu obliczymy z poniższego wzoru:

$$T = 2 \hspace{.05cm} \pi \hspace{.05cm} \sqrt{\frac{\mathstrut L}{g}} = 2 \cdot 3,\hspace{-.1cm}14 \cdot \sqrt{\frac{\mathstrut 0,\hspace{-.1cm}75 \hspace{.05cm} \textrm{m}}{9,\hspace{-.1cm}81 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2}}} = 1,\hspace{-.1cm}74 \hspace{.05cm} \textrm{s}$$

gdzie:
L  – długość wahadła równa odległości punkt zaczepienia nici – środek masy układu,
g  – przyspieszenie ziemskie.

Znając okres drgań układu możemy obliczyć prędkość przesuwu taśmy. Wiemy, że taśma przesuwa się ze stałą prędkością, dlatego korzystając ze wzoru na prędkość w ruchu jednostajnym prostoliniowym, mamy:

$$V_t = \frac{s}{t} = \frac{s}{\tfrac{3}{2} \hspace{.05cm} T} = \frac{30 \hspace{.05cm} \textrm{cm}}{\tfrac{3}{2} \cdot 1,\hspace{-.1cm}74 \hspace{.05cm} \textrm{s}} = 11,5 \hspace{.05cm} \tfrac{\textrm{cm}}{\textrm{s}}$$

gdzie s  to długość o jaką przesunęła się taśma papierowa podczas trwania czasu  $t = \frac{3}{2} \hspace{.05cm} T$  (zobacz rysunek).

Zgodnie z teorią, maksymalna prędkość drgań układu wynosi  $V_{max} = \pm \omega \hspace{.05cm} A$,  w związku z czym:

$$V_{max} = \pm \omega \hspace{.05cm} A = \pm \frac{2 \hspace{.05cm} \pi}{T} \hspace{.05cm} A = \pm \frac{2 \cdot 3,\hspace{-.1cm}14}{1,\hspace{-.1cm}74 \hspace{.05cm} \textrm{s}} \cdot 7 \hspace{.05cm} \textrm{cm} = \pm 25,\hspace{-.1cm}3 \hspace{.05cm} \tfrac{\textrm{cm}}{\textrm{s}}$$

gdzie A  to amplituda drgań układu równa ok. 7 cm (połowa szerokości taśmy wynosi 7,5 cm; przyjmujemy, że amplituda wynosi nieco mniej niż 7,5 cm)

Prawidłowa odpowiedź: T  = 1,74 s, V_t  = 11,5 cm/s, V_max  = ± 25,3 cm/s.

Okres drgań jest proporcjonalny do długości wahadła: im większa długość wahadła, tym większy okres drgań. Wraz ze zmniejszaniem się ilości piasku w naczyniu długość wahadła, tj. odległość punkt zaczepienia nici – środek masy wahadła, ulega zwiększeniu, w związku z czym okres drgań tego układu również będzie wzrastał.

Prawidłowa odpowiedź: C – 1.

Rozwiązania kolejnych zadań z tego arkusza maturalnego znajdziesz na poniższych stronach: