Arkusz maturalny z fizyki – poziom rozszerzony – rok 2016 („nowa matura”) – zadania nr 1 – 4

Dane potrzebne do stworzenia wykresu x (t ) podano w tabeli. Niepewność pomiaru położenia wózka równą ± 5 cm oznaczono na wykresie, dla każdego punktu pomiarowego, za pomocą dwóch linii pionowych o długości 5 cm:

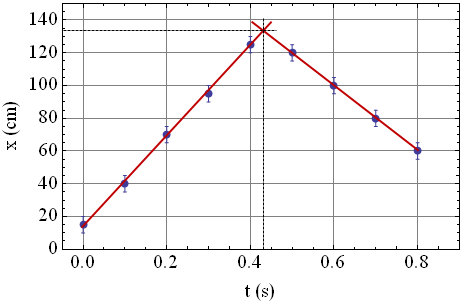
Aby wyznaczyć czas oraz położenie wózka w chwili zderzenia z nieruchomą przeszkodą należy narysować na wykresie x (t ) dwie proste przechodzące przez punkty pomiarowe (czerwone linie na wykresie x (t )) i następnie dla punktu przecięcia się tych dwóch prostych, odczytać czas t  oraz położenie x  (dla czytelności czarnymi liniami zaznaczono miejsca przecięcia się punktu wyznaczonego przez czerwone proste z osiami współrzędnych).

Prawidłowa odpowiedź: t  = 0,43 ÷ 0,44 s, x  = 134 ÷ 135 cm.

Aby dowiedzieć się jaki charakter miało odbicie wózka od przeszkody należy:
– na podstawie danych zamieszczonych w tabeli wyznaczyć, jak zmieniało się położenie wózka w funkcji czasu (wyznaczyć różnicę położenia pomiędzy kolejnymi pomiarami przed i po odbiciu),
– porównać czerwone krzywe na wykresie x (t ).

W tym zadaniu skorzystamy z drugiej opcji. Zwróć uwagę, że nachylenia krzywych różnią się: współczynnik kierunkowy pierwszej krzywej, odpowiadającej sytuacji przed odbiciem, jest większy od współczynnika kierunkowego drugiej krzywej, odpowiadającej sytuacji po odbiciu. Na podstawie tego faktu możemy stwierdzić, że wózek przed odbiciem musiał poruszać się z większą prędkością, niż po odbiciu. Oznacza to, że zderzenie z przeszkodą nie było doskonale sprężyste.

Prawidłowa odpowiedź: zderzenie wózka z przeszkodą nie było zderzeniem doskonale sprężystym.

Produktami rozpadu izotopu radonu  $^{222}_{86} \hspace{.05cm} \textrm{Rn}$  są polon oraz cząstka alfa (oznaczenie α). Cząstka α to zwyczajowe określenia jądra helu  $^4_2 \hspace{.05cm} \textrm{He}$.  Suma liczb masowych A i liczb atomowych Z przed reakcją musi odpowiadać sumie liczb masowych i atomowych po reakcji. Aby wyznaczyć liczbę A i Z dla polonu dokonajmy prostych rachunków:

– liczba masowa polonu: A = 222 – 4 = 218,
– liczba atomowa polonu: Z = 86 – 2 = 84.

Równanie reakcji wygląda więc następująco:

$$^{222}_{86} \hspace{.05cm} \textrm{Rn} \hspace{.2cm} \longrightarrow \hspace{.2cm} ^{218}_{84} \hspace{.05cm} \textrm{Po} + \hspace{.05cm} ^{4}_{2} \hspace{.05cm} \textrm{He}$$

(zamiast  $^4_2 \hspace{.05cm} \textrm{He}$, możemy również wstawić oznaczenie cząstki alfa – α)

Energia spoczynkowa jądra radonu, mająca ścisły związek z jego masą, ulega przekształceniu w produkty reakcji (jądro polonu oraz cząstkę alfa) i energię kinetyczną cząstki alfa. Przekazanie tej dodatkowej energii cząstce α powoduje, że sumaryczna energia spoczynkowa produktów reakcji jest mniejsza od energii spoczynkowej jądra radonu. Masa jest równoważna energii i dlatego masa jądra radonu jest większa od masy produktów reakcji.

Prawidłowa odpowiedź: B – 1.

Zacznijmy od stworzenia odpowiedniego rysunku:

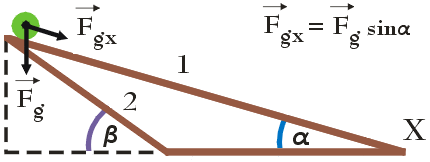
Ruch kulek K1 i K2 po pochylni 1 i 2 odbywa się wskutek działania składowej siły ciężkości F_g,x . Gdy kulka K1 porusza się po pochylni 1 siła ta, zgodnie z rysunkiem, wynosi  $F_{g,x1} = m \hspace{.05cm} g \hspace{.05cm} \textrm{sin} \hspace{.03cm} \alpha$,  a dla kulki K2 poruszającej się po pochylni 2:  $F_{g,x2} = m \hspace{.05cm} g \hspace{.05cm} \textrm{sin} \hspace{.03cm} \beta$  (w miejsce siły ciężkości F_g  wstawiliśmy wyrażenie m g ). Zwróć uwagę, że β  > α. Korzystając z drugiej zasady dynamiki Newtona, dostaniemy:

– dla kulki K1:

$$m \hspace{.05cm} g \hspace{.05cm} \textrm{sin} \hspace{.03cm} \alpha = m \hspace{.05cm} a_1 \hspace{1cm} \longrightarrow \hspace{1cm} a_1 = g \hspace{.05cm} \textrm{sin} \hspace{.03cm} \alpha$$

– dla kulki K2:

$$m \hspace{.05cm} g \hspace{.05cm} \textrm{sin} \hspace{.03cm} \beta = m \hspace{.05cm} a_2 \hspace{1cm} \longrightarrow \hspace{1cm} a_2 = g \hspace{.05cm} \textrm{sin} \hspace{.03cm} \beta$$

Wartość funkcji sinus w przedziale kątów (0^o, 90^o) rośnie wraz ze wzrostem wartości kąta, w związku z czym a₂  > a₁,  ponieważ β  > α. Im większa wartość przyspieszenia, tym większa zmiana (wzrost) prędkości kulki w funkcji czasu. Kulka K2 po stoczeniu się z pochylni 2 będzie poruszać się po linii prostej z maksymalną, stałą prędkością V_2,max. Jak wykażemy w punkcie 3.2 kulka K1 osiągnie prędkość V_1,max  = V_2,max  dopiero w punkcie X, w związku z czym czas toczenia się kulki K2 do punktu X będzie krótszy niż czas toczenia się kulki K1.

Prawidłowa odpowiedź: A – 3.

W tym zadaniu skorzystamy z zasady zachowania energii mechanicznej (mamy zbyt mało danych, aby zastosować drugą zasadę dynamiki Newtona). Gdy kulki K1 i K2 znajdują się na szczycie pochylni 1 i 2, całkowita energia mechaniczna kulek równa się ich energii potencjalnej:  $E_c = E_p = m \hspace{.05cm} g \hspace{.05cm} h$.  Gdy kulki znajdują się w punkcie X, całkowita energia mechaniczna kulek odpowiada ich energii kinetycznej będącej sumą energii kinetycznej ruchu postępowego (kulka zmienia swoje położenie) i ruchu obrotowego (kulka się obraca) kulek:  $E_c = E_{k,post} + E_{k,obr} = \frac{1}{2} \hspace{.05cm} m \hspace{.05cm} V^2 + \frac{1}{2} \hspace{.05cm} I \hspace{.05cm} \omega^2$.  Ponieważ straty energii kulek możemy pominąć, dlatego z porównania tych dwóch energii, dostaniemy:

– dla kulki 1:

$$m \hspace{.05cm} g \hspace{.05cm} h = \tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} V_1^2 + \tfrac{1}{2} \hspace{.05cm} I \hspace{.05cm} \omega_1^2 = \tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} V_1^2 + \tfrac{1}{2} \cdot \tfrac{2}{5} \hspace{.05cm} m \hspace{.05cm} R^2 \hspace{.05cm} \omega_1^2$$

– dla kulki 2:

$$m \hspace{.05cm} g \hspace{.05cm} h = \tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} V_2^2 + \tfrac{1}{2} \hspace{.05cm} I \hspace{.05cm} \omega_2^2 = \tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} V_2^2 + \tfrac{1}{2} \cdot \tfrac{2}{5} \hspace{.05cm} m \hspace{.05cm} R^2 \hspace{.05cm} \omega_2^2$$

gdzie w miejsce momentu bezwładności I  wstawiliśmy wartość podaną w treści zadania:  $I = \frac{2}{5} \hspace{.05cm} m \hspace{.05cm} R^2$.

Prędkość kątowa  $\omega = \frac{V}{R}$,  dlatego:

$$m \hspace{.05cm} g \hspace{.05cm} h = \tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} V_1^2 + \tfrac{1}{2} \cdot \tfrac{2}{5} \hspace{.05cm} m \hspace{.05cm} R^2 \hspace{.05cm} \frac{V_1^2}{R^2} = \left( \tfrac{1}{2} + \tfrac{1}{5} \right) m \hspace{.05cm} V_1^2 = \tfrac{7}{10} \hspace{.05cm} m \hspace{.05cm} V_1^2$$

oraz

$$m \hspace{.05cm} g \hspace{.05cm} h = \tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} V_2^2 + \tfrac{1}{2} \cdot \tfrac{2}{5} \hspace{.05cm} m \hspace{.05cm} R^2 \hspace{.05cm} \frac{V_2^2}{R^2} = \left( \tfrac{1}{2} + \tfrac{1}{5} \right) m \hspace{.05cm} V_2^2 = \tfrac{7}{10} \hspace{.05cm} m \hspace{.05cm} V_2^2$$

Po skróceniu i przekształceniu dwóch powyższych wyrażeń względem prędkości V, otrzymamy:

$$V_1 = \sqrt{\tfrac{\mathstrut 10}{7} \hspace{.05cm} g \hspace{.05cm} h}$$

i

$$V_2 = \sqrt{\tfrac{\mathstrut 10}{7} \hspace{.05cm} g \hspace{.05cm} h}$$

Widzimy więc, że V₁  = V₂. Wartość prędkości zależy od przyspieszenia ziemskiego g  oraz wysokości h, dlatego:

Prawidłowa odpowiedź: B – 2.

Wzór na prędkość V₁  wyprowadziliśmy w zadaniu 3.2. Po podstawieniu wartości liczbowych i wykonaniu obliczeń, dostaniemy:

$$V_1 = \sqrt{\mathstrut \tfrac{10}{7} \cdot 9,\hspace{-.1cm}81 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2} \cdot 0,\hspace{-.1cm}2 \hspace{.05cm} \textrm{m}} = 1,\hspace{-.1cm}67 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}}$$

Prawidłowa odpowiedź: prędkość kulki K1 w punkcie X wynosi V₁  = 1,67 m/s.

Przypadek 1 – tratwa bez ładunku

Tratwa unosi się na powierzchni wody, w związku z czym siła ciężkości  $\vec{P}$  działająca na tratwę musi być równoważona przez siłę wyporu  $\vec{F}$  (jednakowe długości wektorów  $\vec{P}$  i  $\vec{F}$ ):

Przypadek 2 – tratwa z ładunkiem

W tym przypadku tratwa obciążona ładunkiem również unosi się na powierzchni wody, z tym że zanurzenie tratwy jest dużo większe niż w pierwszym przypadku. Siła wyporu  $\vec{F}$  działająca na układ tratwa – ładunek będzie więc równa wypadkowej sił  $\vec{P}$  i  $\vec{Q}$ :

Aby rozwiązać to zadanie przeanalizujemy dwa przypadki: pierwszy przypadek będzie dotyczył tratwy bez ładunku, drugi – tratwy obciążonej ładunkiem (w obu przypadkach tratwa unosi się na wodzie). Siły działające na tratwę nieobciążoną i obciążoną ładunkiem równoważą się, wobec czego:

– tratwa nieobciążona ładunkiem:

$$\vec{F}_{g1} = \vec{F}_{wyp1} \hspace{1cm} \longrightarrow \hspace{1cm} m_t \hspace{.05cm} g = \rho_w \hspace{.05cm} V_1 \hspace{.05cm} g \hspace{1cm} \longrightarrow \hspace{1cm} m_t = \rho_w \hspace{.05cm} V_1$$

gdzie:
m_t  – masa tratwy,
ρ_w  – gęstość wody,
V₁  – objętość wody wypartej przez nieobciążoną tratwę,

– tratwa obciążona ładunkiem:

$$\vec{F}_{g2} = \vec{F}_{wyp2} \hspace{1cm} \longrightarrow \hspace{1cm} \left( m_t + m_{max} \right) g = \rho_w \hspace{.05cm} V_2 \hspace{.05cm} g \hspace{1cm} \longrightarrow \hspace{1cm} m_t + m_{max} = \rho_w \hspace{.05cm} V_2$$

gdzie:
m_max  – maksymalna masa ładunku jaki można umieścić na tratwie,
V₂  – objętość wody wypartej przez układ tratwa – ładunek.

Po przekształceniu powyższego wzoru względem m_max :

$$m_{max} = \rho_w \hspace{.05cm} V_2 \hspace{.15cm} – \hspace{.05cm} m_t$$

i podstawieniu w miejsce  $m_t = \rho_w \hspace{.05cm} V_1$, otrzymamy:

$$m_{max} = \rho_w \hspace{.05cm} V_2 \hspace{.15cm} – \hspace{.05cm} \rho_w \hspace{.05cm} V_1 = \rho_w \left( V_2 \hspace{.15cm} – \hspace{.05cm} V_1 \right)$$

Objętości V₁  i V₂  nie są podane w treści zadania. Możemy je jednak z łatwością wyznaczyć, ponieważ są one równe objętości tratwy znajdującej się pod powierzchnią wody. Gdy tratwa nie jest obciążona ładunkiem  $V_1 = \frac{3}{5} \hspace{.05cm} V_t$, ponieważ  $\dfrac{\rho_d}{\rho_w} \cdot 100 \% = \frac{600 \hspace{.05cm} \frac{\textrm{kg}}{\textrm{m}^3}}{1000 \hspace{.05cm} \frac{\textrm{kg}}{\textrm{m}^3}} \cdot 100 \% = 60 \%$  (40% całkowitej objętości tratwy znajduje się nad powierzchnią wody). W przypadku, gdy tratwa jest obciążona ładunkiem  $V_2 = \frac{3}{4} \hspace{.05cm} V_t$,  bo 25% całkowitej objętości tratwy musi wystawać ponad powierzchnię wody. Po podstawieniu V₁  i  V₂  do równania na m_max, otrzymamy:

$$m_{max} = \rho_w \hspace{.05cm} V_t \left( \tfrac{3}{4} \hspace{.15cm} – \hspace{.05cm} \tfrac{3}{5} \right) = \tfrac{3}{20} \hspace{.05cm} \rho_w \hspace{.05cm} V_t$$

Objętość tratwy V_t  równa jest objętości dziesięciu pni, mających kształt walca, w związku z czym  $V_t = 10 \hspace{.05cm} h \hspace{.05cm} S$,  gdzie h  to wysokość pnia, S  – pole powierzchni podstawy pnia.

Dostaniemy więc:

$$m_{max} = \tfrac{3}{20} \hspace{.05cm} \rho_w \cdot 10 \hspace{.05cm} h \hspace{.05cm} S = \tfrac{3}{2} \hspace{.05cm} \rho_w \hspace{.05cm} h \hspace{.05cm} S$$

skąd po podstawieniu wartości liczbowych oraz wykonaniu obliczeń, otrzymamy:

$$m_{max} = \tfrac{3}{2} \cdot 1000 \hspace{.05cm} \tfrac{\textrm{kg}}{\textrm{m}^3} \cdot 2 \hspace{.05cm} \textrm{m} \cdot 0,\hspace{-.1cm}07 \hspace{.05cm} \textrm{m}^2 = 210 \hspace{.05cm} \textrm{kg}$$

Prawidłowa odpowiedź: maksymalna masa ładunku m_max  = 210 kg.

Rozwiązania kolejnych zadań z tego arkusza maturalnego znajdziesz na poniższych stronach: