Arkusz maturalny z fizyki – poziom rozszerzony – rok 2016 („nowa matura”) – zadania nr 13 – 16

Zastosowanie kulistego źródła światła Z sprawiło, że na ścianie powstały obszary półcienia oraz cienia całkowitego. Cień (C) to obszar, do którego nie docierają promienie świetlne bezpośrednio ze źródła światła. Półcień (P), z kolei, to obszar, do którego docierają promienie świetlne tylko z części powierzchni źródła. Sposób wyznaczenia tych dwóch obszarów został przedstawiony na poniższym rysunku:

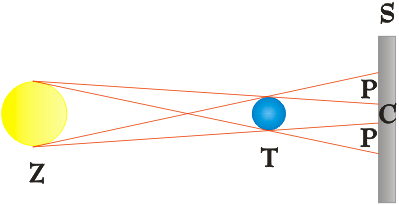
Zdanie 1

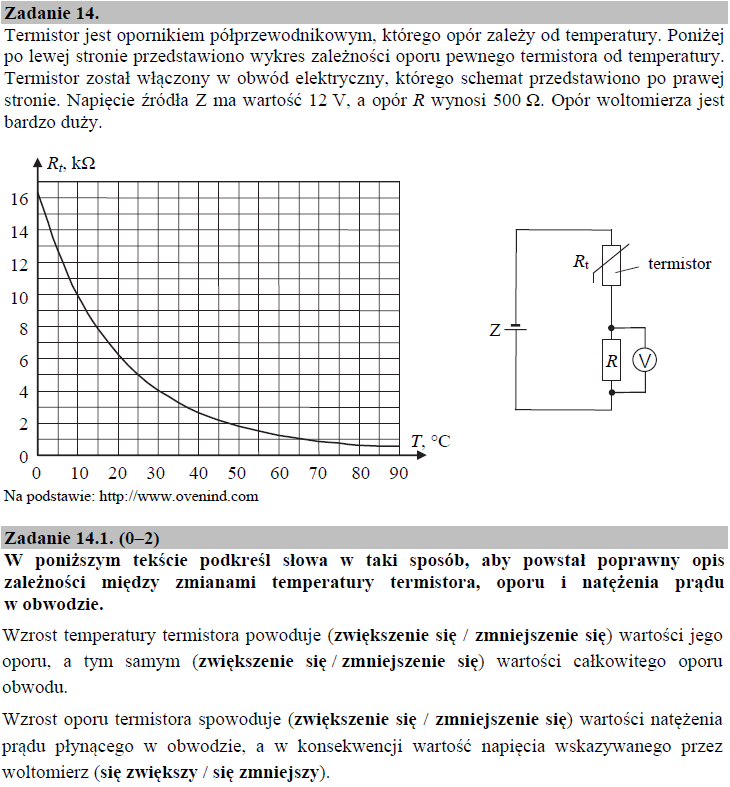
Zgodnie z wykresem opór termistora maleje wraz ze wzrostem temperatury. Mniejsza wartość oporu termistora wpływa oczywiście na zmniejszenie się całkowitej wartości oporu obwodu elektrycznego.

Zdanie 2

Im większa wartość oporu termistora, tym termistor bardziej „przeciwstawia się” przepływowi prądu elektrycznego, w związku z czym wraz ze wzrostem rezystancji R, natężenie prądu płynącego w obwodzie będzie maleć. Podobnie, wskazanie woltomierza będzie mniejsze, ponieważ spadek napięcia na termistorze ulegnie zwiększeniu.

Korzystamy z drugiego prawa Kirchhoffa:

$$Z \hspace{.15cm} – \hspace{.05cm} I \hspace{.03cm} R \hspace{.15cm} – \hspace{.05cm} I \hspace{.03cm} R_t = 0$$

gdzie:
Z  – napięcie źródła,
I  – natężenie prądu płynącego w obwodzie,
R  – rezystancja opornika R,
R_t  – rezystancja opornika R_t.

Po przekształceniu powyższego wzoru względem R_t , dostaniemy:

$$I \left( R + R_t \right) = Z \hspace{1cm} \longrightarrow \hspace{1cm} R_t = \frac{Z}{I} \hspace{.15cm} – \hspace{.05cm} R$$

Wiemy, że spadek napięcia na rezystorze R, zmierzony przez woltomierz, wynosi U  = 3 V. Zgodnie z prawem Ohma  $I = \frac{U}{R}$,  dlatego:

$$R_t = \frac{Z}{\frac{U}{R}} \hspace{.15cm} – \hspace{.05cm} R = R \left( \frac{Z}{U} \hspace{.15cm} – \hspace{.05cm} 1 \right)$$

Po podstawieniu wartości liczbowych oraz wykonaniu obliczeń, otrzymamy:

$$R_t = 500 \hspace{.05cm} \Omega \cdot \left( \frac{12 \hspace{.05cm} \textrm{V}}{3 \hspace{.05cm} \textrm{V}} \hspace{.15cm} – \hspace{.05cm} 1 \right) = 1500 \hspace{.05cm} \Omega = 1,\hspace{-.1cm}5 \hspace{.05cm} \textrm{k}\Omega$$

Wartość R_t  = 1,5 kΩ na wykresie R (T ) odpowiada temperaturze T  = 55^oC, zatem tyle właśnie wynosiła temperatura wody w instalacji centralnego ogrzewania.

Prawidłowa odpowiedź: R_t  = 1,5 kΩ, T  = 55^oC.

Wraz ze wzrostem natężenia prądu przepływającego przez obwód wzrasta również temperatura (ciepło Joule’a – Lenza) elementów składowych obwodu m.in. termistora. Wzrost temperatury termistora sprawi, że pomiar temperatury otoczenia będzie zaburzony (temperatura mierzona przez termistor nie będzie równa temperaturze otoczenia).

Prędkość ucieczki to minimalna prędkość, z jaką musi poruszać się ciało, aby mogło opuścić dowolne ciało niebieskie (np. planetę, czy gwiazdę). Im większa masa oraz im mniejszy promień ciała niebieskiego, tym większa prędkość ucieczki. Aby obliczyć wartość prędkości ucieczki z Układu Słonecznego dla obiektu znajdującego się w odległości 1 j.a. od Słońca skorzystamy z zasady zachowania energii (prędkość ta w praktyce odpowiada prędkości ucieczki względem Słońca, skupiającego większość masy Układu Słonecznego, dlatego w obliczeniach weźmiemy pod uwagę tylko energię kinetyczną związaną z obiektem oraz grawitacyjną energię potencjalną układu obiekt – Słońce):

$$E_{k1} + E_{p1} = E_{k2} + E_{p2}$$

gdzie:
E_k1  i E_k2  to odpowiednio energia kinetyczna obiektu przed i po nadaniu mu prędkości ucieczki (założyliśmy, że zmiana energii kinetycznej Słońca, ze względu na ogromną masę, jest na tyle mała, że możemy ją zaniedbać),
E_p1  i E_p2  – grawitacyjna energia potencjalna układu obiekt – Słońce przed i po nadaniu obiektowi prędkości ucieczki.

Obiekt poruszający się z prędkością ucieczki V_u  zatrzyma się (przynajmniej w teorii) w nieskończonej odległości od Słońca, zatem energia kinetyczna E_k2  i grawitacyjna energia potencjalna E_p2  będą równe zero. Zgodnie z zasadą zachowania energii, całkowita energia układu izolowanego (zakładamy, że układ obiekt – Słońce jest takim właśnie układem) pozostaje stała, w związku z czym energia początkowa układu E_k1  + E_p1  musi być także równa zero:

$$E_{k1} + E_{p1} = 0 \hspace{1cm} \longrightarrow \hspace{1cm} E_{k1} = \hspace{.15cm} – \hspace{.05cm} E_{p1}$$

Po podstawieniu w miejsce E_k1  i E_p1  wyrażeń na energię kinetyczną i grawitacyjną energię potencjalną, dostaniemy:

$$\frac{m \hspace{.05cm} V_U^2}{2} = \hspace{.15cm} – \hspace{.05cm} \left( \hspace{.15cm} – \hspace{.05cm} G \hspace{.05cm} \frac{m \hspace{.05cm} M_S}{r} \right) = G \hspace{.05cm} \frac{m \hspace{.05cm} M_S}{r}$$

gdzie:
m  i Vu  to odpowiednio masa oraz prędkość ucieczki obiektu z Układu Słonecznego,
G – stała grawitacji równa 6,67 ⋅ 10^-11 N ⋅ m²/kg²,
M_S  – masa Słońca,
r  – odległość obiektu od Słońca.

Po skróceniu oraz przekształceniu powyższego wyrażenia względem V_u , otrzymamy:

$$V_u = \sqrt{\frac{\mathstrut 2 \hspace{.05cm} G \hspace{.05cm} M_S}{r}}$$

Po podstawieniu wartości liczbowych oraz wykonaniu obliczeń, mamy:

$$V_u = \sqrt{\frac{\mathstrut 2 \cdot 6,\hspace{-.1cm}67 \cdot 10^{-11} \hspace{.05cm} \tfrac{\textrm{N} \hspace{.05cm} \cdot \hspace{.05cm} \textrm{m}^2}{\textrm{kg}^2} \cdot 336000 \cdot 5,\hspace{-.1cm}98 \cdot 10^{24} \hspace{.05cm} \textrm{kg}}{150 \cdot 10^9 \hspace{.05cm} \textrm{m}}} = 42,\hspace{-.1cm}3 \hspace{.05cm} \tfrac{\textrm{km}}{\textrm{s}}$$

Prawidłowa odpowiedź: prędkość ucieczki V_u  = 42,3 km/s.

Zgodnie z tekstem do zadania 15, składowa równoległa prędkości sondy w fazie oddalania się od Jowisza wzrośnie o podwojoną wartość prędkości Jowisza. W związku z tym faktem, maksymalna prędkość sondy względem Słońca, po zastosowaniu asysty grawitacyjnej, może wynieść:

$$V_{s,max} = V_s + 2 \hspace{.05cm} V_J = 10 \hspace{.05cm} \tfrac{\textrm{km}}{\textrm{s}} + 2 \cdot 13 \hspace{.05cm} \tfrac{\textrm{km}}{\textrm{s}} = 36 \hspace{.05cm} \tfrac{\textrm{km}}{\textrm{s}}$$

Prawidłowa odpowiedź: maksymalna prędkość sondy V_s,max  = 36 km/s.

Zjawisko asysty grawitacyjnej wykorzystuje zjawisko przekazania (bardzo niewielkiej) części energii kinetycznej dużego ciała niebieskiego (np. planety) dużo mniejszemu obiektowi np. sondzie.

Prawidłowa odpowiedź: C.

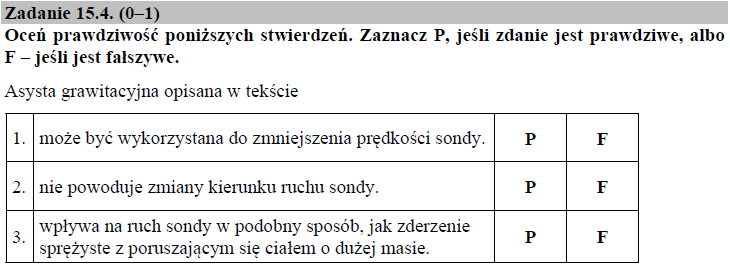
Zdanie 1

Jak wynika z tekstu do zadania 15, asysta grawitacyjna może być wykorzystana do zmniejszenia prędkości sondy, ponieważ przy zbliżaniu się sondy do planety, składowa równoległa prędkości sondy maleje o wartość prędkości planety.

Zdanie 2

Na tor ruchu sondy wpływa oddziaływanie grawitacyjne występujące pomiędzy sondą a planetą. Im mniejsza odległość od planety, tym większa wartość siły oddziaływania grawitacyjnego i tym większe zakrzywienie toru ruchu sondy.

Zdanie 3

Podczas oddalania się sondy od planety, prędkość sondy, a więc także i energia kinetyczna, wzrasta. Pomimo braku bezpośredniego kontaktu między sondą a planetą, sonda zwiększa swoją prędkość w podobny sposób jak ciało o małej masie zderzające się sprężyście z ciałem o bardzo dużej masie (nie występuje tu zmiana zwrotu wektora prędkości sondy o 180^o, lecz, jak napisaliśmy wyżej, kierunek ruchu sondy ulega wyraźnej zmianie).

Prawidłowa odpowiedź: 1 – P,  2 – F,  3 – P.

Dla częstotliwości f₁  = 50 Hz napięcie skuteczne U₁  = 240 V. Dla częstotliwości f₂ napięcie skuteczne U₂ będzie równe (korzystamy z proporcji):

$$U_2 = \frac{f_2 \hspace{.1cm} U_1}{f_1} = \frac{60 \hspace{.05cm} \textrm{Hz} \cdot 240 \hspace{.05cm} \textrm{V}}{50 \hspace{.05cm} \textrm{Hz}} = 288 \hspace{.05cm} \textrm{V}$$

Prawidłowa odpowiedź: U  = 288 V.

Rozwiązania kolejnych zadań z tego arkusza maturalnego znajdziesz na poniższych stronach: