Arkusz maturalny z fizyki – poziom rozszerzony – rok 2016 („nowa matura”) – zadania nr 9 – 12

Prędkość dźwięku w powietrzu wynosi ok. 340 m/s (ok. 1220 km/h), a prędkość światła ok. 3 ⋅ 10⁸ m/s (ok. 11 ⋅ 10⁸ km/h). Wielkość efektu Dopplera zależy od stosunku prędkości źródła wytwarzającego fale do prędkości, z jaką fale te rozchodzą się w danym ośrodku. Załóżmy, że karetka porusza się z prędkością V  = 100 km/h. Prędkość karetki stanowi ok. 8% prędkości dźwięku oraz 0,00001% prędkości światła. To właśnie dlatego udaje nam się doświadczać tylko akustycznego efektu Dopplera.

Zgodnie z teorią wektor natężenia pola elektrycznego  $\vec{E}$  jest zawsze zwrócony od ładunku q, jeśli ładunek q  jest dodatni oraz do ładunku q, jeśli ładunek q  jest ujemny. Korzystając z tej informacji, otrzymamy:

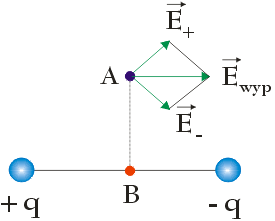
(wektor natężenia pola  $\vec{E}_{wyp}$  w punkcie A wyznaczyliśmy korzystając z metody równoległoboku)

Zacznijmy od stworzenia rysunku schematycznego:

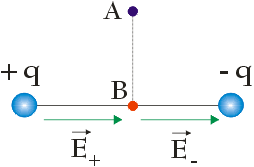
Dla czytelności umieśćmy początek wektora  $\vec{E_+}$  w pobliżu punktu B (obydwa wektory mają początek w punkcie B, jednak, aby zwiększyć czytelność rysunku umieściliśmy je w pobliżu punktu B):

Zgodnie z powyższym rysunkiem  $\vec{E}_{wyp} = \vec{E}_{+} + \vec{E}_{-}$ .  Ponieważ,  $E = \dfrac{|q|}{4 \hspace{.05cm} \pi \hspace{.05cm} \varepsilon_0 \hspace{.05cm} r^2}$,  gdzie r  to odległość od ładunku do punktu B równa  $r = \frac{1}{2} \hspace{.05cm} d$, dostaniemy:

$$E_{wyp} = \frac{q}{4 \hspace{.05cm} \pi \hspace{.05cm} \varepsilon_0 \cdot \left( \tfrac{1}{2} \hspace{.05cm} d \right)^2} + \frac{q}{4 \hspace{.05cm} \pi \hspace{.05cm} \varepsilon_0 \cdot \left( \tfrac{1}{2} \hspace{.05cm} d \right)^2} = \frac{2 \hspace{.05cm} q}{4 \hspace{.05cm} \pi \hspace{.05cm} \varepsilon_0 \cdot \tfrac{1}{4} \hspace{.05cm} d^2} = \frac{2 \hspace{.05cm} q}{\pi \hspace{.05cm} \varepsilon_0 \hspace{.05cm} d^2}$$

Po podstawieniu wartości liczbowych oraz wykonaniu obliczeń, uzyskamy:

$$E_{wyp} = \frac{2 \cdot 10^{-12} \hspace{.05cm} \textrm{C}}{3,\hspace{-.1cm}14 \cdot 8,\hspace{-.1cm}85 \cdot 10^{-12} \hspace{.05cm} \tfrac{\textrm{F}}{\textrm{m}} \cdot \left( 10^{-2} \hspace{.05cm} \textrm{m} \right)^2} = 720 \hspace{.05cm} \tfrac{\textrm{N}}{\textrm{C}}$$

Prawidłowa odpowiedź: natężenie pola elektrycznego w punkcie B wynosi E  = 720 N/C.

Siły elektrostatyczne działają na ładunki wzdłuż linii pola elektrostatycznego. Linie sił pola zwrócone są od ładunku dodatniego i do ładunku ujemnego, dlatego w przypadku rysunku a) i b) ładunek dodatni „zgromadzony” jest po lewej stronie linii pola, a ładunek ujemny po stronie prawej. Oznacza to, że w przypadku a) dipol obróci się w polu w kierunku przeciwnym do ruchu wskazówek zegara (dipol ustawi się równolegle do linii sił pola). W przypadku b) – niejednorodne pole – dipol będzie stopniowo przesuwał się w lewo, w stronę silniejszego pola elektrostatycznego.

Jak podano w głównej części zadania, elektryczny moment dipolowy  $\vec{p}$  cząsteczki wyraża się wzorem  $\vec{p} = q \hspace{.05cm} \vec{d}$.  Wiemy, że w przypadku cząsteczki HCl ładunek elektronowy q  = e  (1 e  = 1,6021 ⋅ 10^-19 C) jest przesunięty względem dodatnio naładowanego jądra atomu wodoru. Załóżmy, że odległość między jądrem a elektronem jest równa połowie odległości między jądrami atomu wodoru i chloru (odległość pomiędzy ładunkami jest mniejsza od odległości pomiędzy jądrami). Dostaniemy wówczas:

$$p = e \cdot \tfrac{1}{2} \hspace{.05cm} d = 1,\hspace{-.1cm}6021 \cdot 10^{-19} \hspace{.05cm} \textrm{C} \cdot \tfrac{1}{2} \cdot 1,\hspace{-.1cm}27 \cdot 10^{-10} \hspace{.05cm} \textrm{m} \approx 10^{-29} \hspace{.05cm} \textrm{C} \cdot \textrm{m}$$

Wynik mamy wyrazić w debajach, dlatego:

$$p = 10^{-29} \hspace{.05cm} \textrm{C} \cdot \textrm{m} \approx 3 \hspace{.05cm} \textrm{D}$$

Prawidłowa odpowiedź: moment dipolowy cząsteczki HCl wynosi p  = 3 D.

Zakładamy, że gaz zamknięty w metalowym cylindrze podlega przemianie izobarycznej, czyli przemianie, podczas której ciśnienie gazu nie ulega zmianie. Zapisując równanie stanu gazu dla tej przemiany przed i po podgrzaniu wody, otrzymamy:

$$\frac{V_1}{T_1} = \frac{V_2}{T_2}$$

gdzie:
V₁  i T₁  to odpowiednio początkowa objętość i temperatura gazu,
V₂  i T₂  to odpowiednio końcowa objętość i temperatura gazu.

Aby wyznaczyć temperaturę zera bezwzględnego w skali Celsjusza wprowadźmy do powyższego wzoru wielkość  $\Delta T = T_{Z (K)} \hspace{.15cm} – \hspace{.05cm} T_{Z (C)}$,  gdzie  $T_{Z (K)}$  to temperatura zera bezwzględnego w skali Kelvina równa 0 K,  $T_{Z (C)}$  – szukana temperatura zera bezwzględnego w skali Celsjusza.

Po podstawieniu, dostaniemy:

$$\frac{V_1}{\Delta \hspace{.03cm} T + T_1} = \frac{V_2}{\Delta \hspace{.03cm} T + T_2}$$

Zauważ, że po wprowadzeniu czynnika ΔT,  temperatury w mianowniku będą, zgodnie z przyjętymi oznaczeniami, odpowiadać temperaturze w skali Kelvina.

Po przemnożeniu stronami i przekształceniu względem ΔT,  mamy:

$$\left( \Delta \hspace{.03cm} T + T_2 \right) V_1 = \left( \Delta \hspace{.03cm} T + T_1 \right) V_2 \hspace{1cm} \longrightarrow \hspace{1cm} \Delta \hspace{.03cm} T = \frac{T_1 \hspace{.05cm} V_2 \hspace{.15cm} – \hspace{.05cm} T_2 \hspace{.05cm} V_1}{V_1 \hspace{.15cm} – \hspace{.05cm} V_2}$$

Po podstawieniu do powyższego wzoru wartości liczbowych oraz wykonaniu obliczeń, uzyskamy:

$$\Delta \hspace{.03cm} T = \frac{22 \hspace{.05cm} ^{\textrm{o}}\textrm{C} \cdot 144 \hspace{.05cm} \textrm{cm}^3 \hspace{.15cm} – \hspace{.05cm} 68 \hspace{.05cm} ^{\textrm{o}}\textrm{C} \cdot 125 \hspace{.05cm} \textrm{cm}^3}{125 \hspace{.05cm} \textrm{cm}^3 \hspace{.15cm} – \hspace{.05cm} 144 \hspace{.05cm} \textrm{cm}^3} = 281 \hspace{.05cm} ^{\textrm{o}}\textrm{C}$$

Ponieważ,  $\Delta T = T_{Z (K)} \hspace{.15cm} – \hspace{.05cm} T_{Z (C)}$,  dlatego:

$$\Delta \hspace{.03cm} T = T_{Z (K)} \hspace{.15cm} – \hspace{.05cm} T_{Z (C)} = 0 \hspace{.05cm} \textrm{K} \hspace{.15cm} – \hspace{.05cm} T_{Z (C)} = \hspace{.15cm} – \hspace{.05cm} T_{Z (C)} \hspace{1cm} \longrightarrow \hspace{1cm} T_{Z (C)} = \hspace{.15cm} – \hspace{.05cm} \Delta \hspace{.03cm} T = \hspace{.15cm} – \hspace{.05cm} 281 \hspace{.05cm} ^{\textrm{o}}\textrm{C}$$

Dla przypomnienia dokładna wartość temperatury zera bezwzględnego w skali Celsjusza wynosi -273,15 ^oC.

Korzystamy z prawa załamania światła (prawa Snella), zgodnie z którym:

$$n_1 \hspace{.05cm} \textrm{sin} \hspace{.03cm} \alpha = n_2 \hspace{.05cm} \textrm{sin} \hspace{.03cm} \beta$$

gdzie:
n₁  – współczynnik załamania powietrza,
α  – kąt padania światła laserowego,
n₂  – współczynnik załamania pryzmatu I,
β  – kąt załamania światła.

Kąt α  i β  wyznaczamy zawsze względem normalnej, czyli prostej prostopadłej do płaszczyzny padania (niebieska, przerywana linia):

Zgodnie z rysunkiem α  = 40^o (90^o – 50^o),  β  = 20^o (90^o – 70^o). Wiemy, że n₁  = 1, w związku z czym:

$$n_2 = \frac{n_1 \hspace{.05cm} \textrm{sin} \hspace{.03cm} \alpha}{\textrm{sin} \hspace{.03cm} \beta} = \frac{\textrm{sin} \hspace{.03cm} \alpha}{\textrm{sin} \hspace{.03cm} \beta} = \frac{\textrm{sin} \hspace{.03cm} 40^{\textrm{o}}}{\textrm{sin} \hspace{.03cm} 20^{\textrm{o}}} = 1,\hspace{-.1cm}88$$

Prawidłowa odpowiedź: współczynnik załamania pryzmatu I wynosi 1,88.

Aby dowiedzieć się czy pryzmat II ma większy/mniejszy współczynnik załamania światła niż pryzmat I, należy poprowadzić normalną do powierzchni granicznej tych dwóch pryzmatów (fioletowa, przerywana linia na rysunku w punkcie a). Zauważ, że promień załamany (przez pryzmat II) jest odchylony od normalnej bardziej (większy kąt do normalnej) niż promień padający (mniejszy kąt do normalnej) na powierzchnię graniczną pryzmatów. Oznacza to, że współczynnik załamania pryzmatu II jest mniejszy niż współczynnik załamania pryzmatu I, co udowodnimy w punkcie c).

Z prawa załamania światła mamy:

$$n_2 \hspace{.05cm} \textrm{sin} \hspace{.03cm} \gamma = n_3 \hspace{.05cm} \textrm{sin} \hspace{.03cm} \theta$$

gdzie:
n₂  – współczynnik załamania pryzmatu I,
γ  – kąt padania,
n₃  – współczynnik załamania pryzmatu II,
θ  – kąt załamania.

Ponieważ n₂  = 1,88, γ  = 20^o, θ  = 25^o, dlatego:

$$n_3 = \frac{n_2 \hspace{.05cm} \textrm{sin} \hspace{.03cm} \gamma}{\textrm{sin} \hspace{.03cm} \theta} = \frac{1,\hspace{-.1cm}88 \cdot \textrm{sin} \hspace{.03cm} 20^{\textrm{o}}}{\textrm{sin} \hspace{.03cm} 25^{\textrm{o}}} = 1,\hspace{-.1cm}52$$

Prawidłowa odpowiedź: współczynnik załamania pryzmatu II wynosi 1,52.

Rozwiązania kolejnych zadań z tego arkusza maturalnego znajdziesz na poniższych stronach: