Arkusz maturalny z fizyki – poziom rozszerzony – rok 2020 („nowa matura”) – zadania nr 1 – 4

Krążek, po uderzeniu przez hokeistę, poruszał się ruchem jednostajnie opóźnionym po linii prostej, dlatego, aby obliczyć czas ruchu krążka skorzystamy ze wzorów na prędkość oraz drogę w ruchu jednostajnie przyspieszonym, podstawiając w miejsce przsypieszenia a  wielkość –a :

$$ V_k = V_0 + a \hspace{.05cm} t = V_0 \hspace{.1cm} – \hspace{.1cm} a \hspace{.05cm} t \\[10pt]
s = V_0 \hspace{.08cm} t + \tfrac{1}{2} \hspace{.05cm} a \hspace{.05cm} t^2 = V_0 \hspace{.08cm} t \hspace{.1cm} – \hspace{.1cm} \tfrac{1}{2} \hspace{.05cm} a \hspace{.05cm} t^2$$

Wiemy, że prędkość początkowa krążka V₀ = V₁ = 14 m/s, droga przebyta przez krążek s  = s₁ = 28 m, a prędkość końcowa V_k  = 0 m/s (krążek zatrzymuje się), dlatego też:

$$ 0 = V_1 \hspace{.1cm} – \hspace{.1cm} a \hspace{.05cm} t_1 \hspace{1cm} \longrightarrow \hspace{1cm} V_1 = a \hspace{.05cm} t_1 \\[10pt]
s_1 = V_1 \hspace{.08cm} t_1 \hspace{.1cm} – \hspace{.1cm} \tfrac{1}{2} \hspace{.05cm} a \hspace{.05cm} t_1^2$$

Wielkością szukaną w zadaniu jest czas ruchu krążka t₁.  Aby obliczyć wartość t₁  przkeształcimy wyrażenie V₁ = a t₁  względem przyspieszenia a :

$$V_1 = a \hspace{.05cm} t_1 \hspace{1cm} \longrightarrow \hspace{1cm} a =\frac{V_1}{t_1}$$

i następnie podstawimy je do wzoru na drogę s₁:

$$s_1 = V_1 \hspace{.08cm} t_1 \hspace{.1cm} – \hspace{.1cm} \tfrac{1}{2} \cdot \frac{V_1}{t_1} \cdot \hspace{.05cm} t_1^2 = V_1 \hspace{.08cm} t_1 \hspace{.1cm} – \hspace{.1cm} \tfrac{1}{2} \hspace{.05cm} V_1 \hspace{.05cm} t_1 = \tfrac{1}{2} \hspace{.05cm} V_1 \hspace{.05cm} t_1$$

Po przekształceniu powyższego wzoru względem czasu t₁, podstawieniu wartości liczbowych i wykonaniu obliczeń, otrzymamy:

$$s_1 = \tfrac{1}{2} \hspace{.05cm} V_1 \hspace{.05cm} t_1 \hspace{1cm} \longrightarrow \hspace{1cm} t_1 = \frac{2 \hspace{.05cm} s_1}{V_1} = \frac{2 \cdot 28 \hspace{.05cm} \textrm{m}}{14 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}}} = 4 \hspace{.05cm} \textrm{s}$$

Prawidłowa odpowiedź: czas ruchu krążka t₁ = 4 s.

Aby obliczyć drogę s₂  przebytą przez krążek poruszający się z prędkością  $V_2 = \tfrac{1}{2} \hspace{.05cm} V_1$  skorzystamy tym razem z zasady zachowania energii. Zgodnie z informacją zawartą we wstępie tego zadania jedyną siłą działającą na krążek podczas jego ruchu po powierzchni lodu jest siła tarcia kinetycznego  $\vec{F}_{Tk}$ , o której wiemy, że przyjmuje stałą wartość, proporcjonalną do ciężaru krążka. Oznacza to, że w jednym oraz w drugim przypadku siła ta wykonuje taką samą pracę. Siła tarcia kinetycznego, działając przeciwnie do kierunku ruchu krążka, powoduje stopniowe zmniejszanie jego prędkości, co przekłada się bezpośrednio na zmniejszanie się jego energii kinetycznej. W związku z powyższym możemy zapisać, że:

$$\Delta \hspace{.05cm} E_k = \hspace{.1cm} – \hspace{.1cm} W_{Tk}$$

gdzie ΔE_k  to zmiana energii kinetycznej krążka, a W_Tk  to praca wykonana przez siłę tarcia kinetycznego.

Korzystając ze wzorów na energię kinetyczną oraz pracę, mamy:

$$\tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} \left( V_k \hspace{.1cm} – \hspace{.1cm} V_0 \right)^2 = \hspace{.1cm} – \hspace{.1cm} F_{Tk} \hspace{.09cm} s$$

W jednym oraz w drugim przypadku prędkość końcowa krążka V_k  = 0 m/s, w związku z czym:

– pierwszy przypadek:

$$\tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} \left( 0 \hspace{.1cm} – \hspace{.1cm} V_1 \right)^2 = \hspace{.1cm} – \hspace{.1cm} F_{Tk} \hspace{.09cm} s_1 \hspace{1cm} \longrightarrow \hspace{1cm} \tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} V_1^2 = F_{Tk} \hspace{.09cm} s_1$$

– drugi przypadek:

$$\tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} \left( 0 \hspace{.1cm} – \hspace{.1cm} V_2 \right)^2 = \hspace{.1cm} – \hspace{.1cm} F_{Tk} \hspace{.09cm} s_2 \hspace{1cm} \longrightarrow \hspace{1cm} \tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} V_2^2 = F_{Tk} \hspace{.09cm} s_2$$

Z pierwszego równania dostaniemy:  $F_{Tk} = \dfrac{\tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} V_1^2}{s_1}$ . Po podstawieniu tego wyrażenia do drugiego wzoru, otrzymamy:

$$\tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} V_2^2 = \dfrac{\tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} V_1^2}{s_1} \hspace{.05cm} s_2 \hspace{1cm} \longrightarrow \hspace{1cm} \frac{s_2}{s_1} = \frac{V_2^2}{V_1^2} = \left( \frac{V_2}{V_1} \right)^2$$

Wiemy, że  $V_2 = \tfrac{1}{2} \hspace{.05cm} V_1$ , zatem:

$$\frac{s_2}{s_1} = \frac{V_2^2}{V_1^2} = \left( \frac{V_2}{V_1} \right)^2 = \frac{V_2^2}{V_1^2} = \left( \frac{\tfrac{1}{2} \hspace{.05cm} V_1}{V_1} \right)^2 = \tfrac{1}{4}$$

Droga s₁ = 28 m, w związku z czym:

$$s_2 = \tfrac{1}{4} \hspace{.05cm} s_1 = \tfrac{1}{4} \cdot 28 \hspace{.05cm} \textrm{m} = 7 \hspace{.05cm} \textrm{m}$$

Prawidłowa odpowiedź: droga przebyta przez krążek wyniosła s₂ = 7 m.

Korzystamy z drugiej zasady dynamiki Newtona. Jak napisaliśmy w zadaniu 1.2 jedyną siłą działającą na krążek jest siła tarcia kinetycznego  $\vec{F}_{Tk}$ , dlatego:

$$\vec{F}_{wyp} = m \hspace{.05cm} \vec{a} \hspace{1cm} \longrightarrow \hspace{1cm} \vec{F}_{Tk} = m \hspace{.05cm} \vec{a}$$

Siła  $\vec{F}_{Tk}$  jest proporcjonalna do ciężaru krążka, tak więc:

$$\mu \hspace{.05cm} m \hspace{.05cm} g = m \hspace{.05cm} a$$

gdzie μ to współczynnik tarcia kinetycznego, a g  – przyspieszenie ziemskie.

Po skróceniu i odwróceniu stronami powyższego wzoru, mamy:

$$a = \mu \hspace{.05cm} g$$

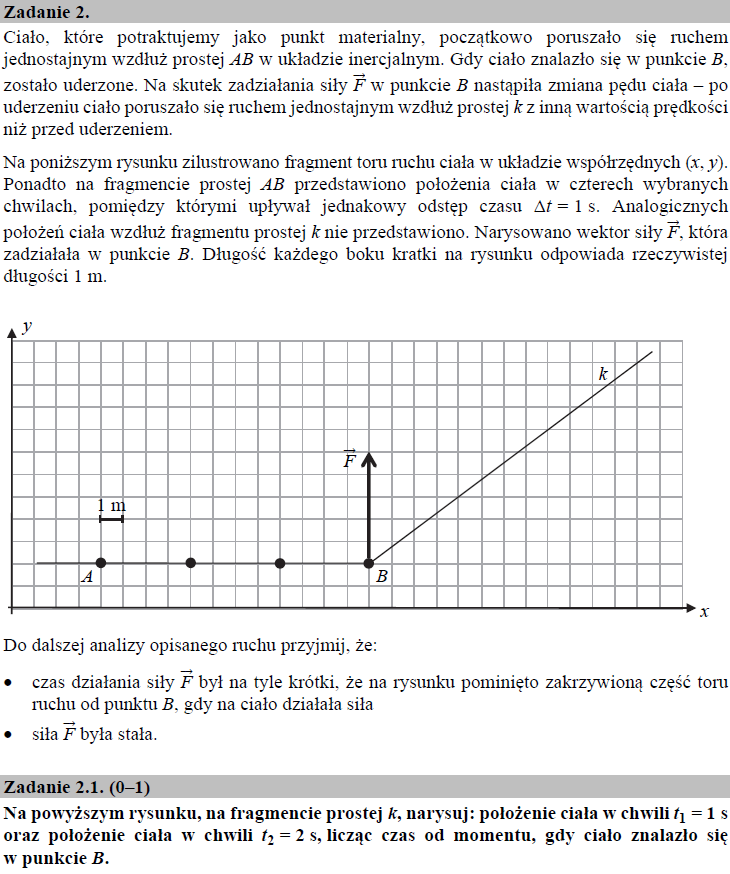
Ruch ciała począwszy od punktu B  jest złożeniem dwóch ruchów: ruchu w kierunku poziomym tj. wzdłuż osi x  oraz ruchu w kierunku pionowym tj. wzdłuż osi y.  Aby wyznaczyć położenie ciała w chwili t₁ = 1 s oraz t₂ = 2 s, od momentu, gdy ciało to znalazło się w punkcie B , skorzystamy z faktu, że siła  $\vec{F}$  działając na ciało pod kątem prostym, a więc prostopadle do początkowego kierunku ruchu ciała nie spowodowała zmiany wartości prędkości tego ciała w kierunku poziomym.

Ruch ciała w kierunku poziomym stanowi kontynuację jego ruchu przed uderzeniem (ruch jednostajny prostoliniowy), a więc podczas każdej sekundy ruchu ciało pokona wzdłuż osi x  odległość równą czterem kratkom. Gdy zaznaczymy te dwa położenia ciała na wykresie i następnie od tych punktów poprowadzimy pionowe linie ku górze wykresu, to miejsca przecięcia tych linii z prostą k  wyznaczą nam położenia ciała w chwilach t₁ i t₂  (dwa fioletowe punkty na prostej k  ).

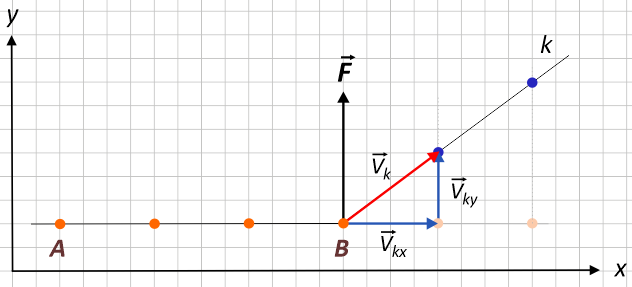
Prędkość  $\vec{V}_k$  tego ciała jest złożeniem składowej poziomej  $\vec{V}_{kx}$  oraz składowej pionowej  $\vec{V}_{ky}$ :

$$V_k = \sqrt{V_{kx}^2 + V_{ky}^2}$$

Zgodnie z wykresem zamieszczonym w zadaniu 2.1 składowa pozioma V_kx  wynosi 4 m/s, ponieważ ciało podczas każdej sekundy ruchu pokonuje w poziomie odległość równą 4 m (odległość ta odpowiada czterem kratkom na wykresie, a każda kratka ma długość 1 m). Składowa pionowa prędkości V_ky  jest równa 3 m/s, ponieważ ciało w pionie pokonuje podczas każdej sekundy ruchu odległość równą 3 m (trzy kratki).

Znając wartość V_kx  i V_ky  możemy przystąpić do obliczenia wartości prędkości V_k :

$$V_k = \sqrt{V_{kx}^2 + V_{ky}^2} = \sqrt{\left( 4 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}} \right)^2 + \left( 3 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}} \right)^2} = \sqrt{25 \hspace{.05cm} \tfrac{\textrm{m}^2}{\textrm{s}^2}} = 5 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}}$$

Prawidłowa odpowiedź: ciało poruszało się wzdłuż prostej k  z prędkością V_k  = 5 m/s.

Zacznijmy od zapisania wzoru opisującego drugą zasadę dynamiki Newtona (zobacz: Pęd ciała)

$$\vec{F} = \dfrac{\Delta \hspace{.05cm} \vec{p}}{\Delta \hspace{.05cm} t}$$

gdzie  $\Delta \hspace{.05cm} \vec{p}$  to zmiana pędu ciała w czasie  $\Delta \hspace{.05cm} t$ .

Pęd to wielkość fizyczna równa iloczynowi masy i prędkości ciała (p = m V ), dlatego też:

$$\Delta \hspace{.05cm} p = m \hspace{.05cm} \Delta \hspace{.02cm} V$$

W naszym przypadku zmiana prędkości ΔV  ciała odpowiada zmianie prędkości ciała w kierunku pionowym (ΔV  = V_y ), bo właśnie w tym kierunku działała na ciało siła  $\vec{F}$  powodująca zmianę prędkości ciała. Mamy więc:

$$\vec{F}_{wyp} = \vec{F} = \dfrac{\Delta \hspace{.05cm} \vec{p}}{\Delta \hspace{.05cm} t_B} = \dfrac{m \hspace{.05cm} \Delta \hspace{.02cm} \vec{V}}{\Delta \hspace{.05cm} t_B} = \dfrac{m \hspace{.05cm} \vec{V}_y}{\Delta \hspace{.05cm} t_B}$$

Po podstawieniu do powyższego wzoru wartości liczbowych oraz wykonaniu obliczeń, dostaniemy:

$$F = \dfrac{0,\hspace{-.05cm}2 \hspace{.05cm} \textrm{kg} \cdot 3 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}}}{0,\hspace{-.05cm}01 \hspace{.05cm} \textrm{s}} = 60 \hspace{.05cm} \textrm{N}$$

Prawidłowa odpowiedź: siła działająca na krążek była równa F = 60 N.

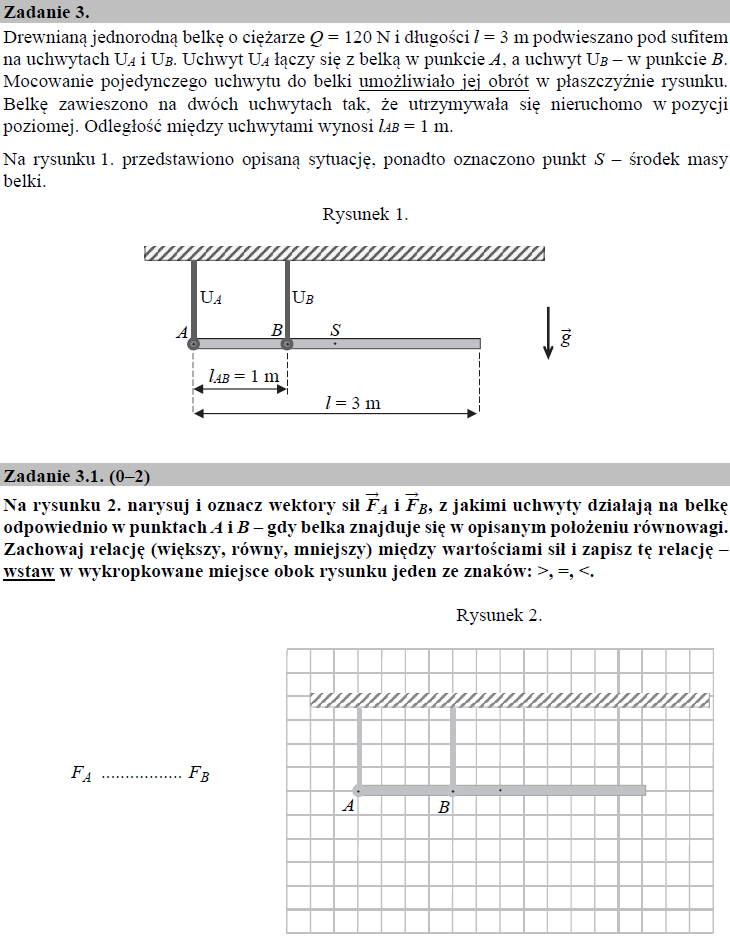
Belka znajduje się stanie równowagi statycznej, a więc wszystkie siły działające na belkę równoważą się (siła wypadkowa jest równa zero). Tymi siłami są: skierowana pionowo w dół siła cieżkości  $\vec{F_g}$  równa ciężarowi belki  $\vec{Q}$ , oraz siły  $\vec{F_A}$  i  $\vec{F_B}$  działające pionowo na belkę ze strony uchwytów. Aby określić zwrot oraz wartość siły  $\vec{F_A}$  i  $\vec{F_B}$  wyobraźmy sobie sytuację, w której na belkę działa tylko siła  $\vec{F_B}$  (zakładamy, że do belki w punkcie A nie jest zamocowany żaden uchwyt). W takiej sytuacji siła  $\vec{F_B}$  musi równoważyć siłę ciężkości  $\vec{Q}$ , w związku z czym jej wartość musi odpowiadać wartości siły  $\vec{Q}$  oraz dodatkowo jej zwrot musi być przeciwny do zwrotu siły ciężkości. Belka zamocowana w ten sposób do sufitu będzie mogła, po przyłożeniu dodatkowej siły, obracać się w płaszczyźnie rysunku.

Aby belka mogła znajdować się w położeniu przedstawionym na powyższym rysunku, siła  $\vec{F_A}$ , działająca na belkę ze strony uchwytu U_A , będzie musiała mieć kierunek i zwrot zgodny z kierunkiem i zwrotem siły ciężkości  $\vec{Q}$ . Dodatkowo, wartość tej siły będzie mniejsza od wartości siły  $\vec{F_B}$  (możesz sobie wyobrazić, że na sile  $\vec{F_B}$  "spoczywa" jak gdyby "główny ciężar" przeciwstawiający się sile ciężkości  $\vec{Q}$ , a siła  $\vec{F_A}$  jest takim jakby dodatkiem pozwalającym belce znajdować się w położeniu poziomym).

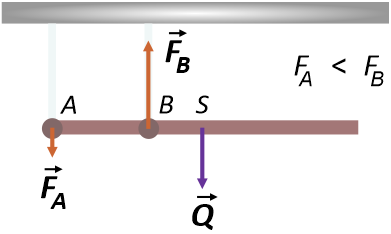
Dla ciała znajdującego się w stanie równowagi statycznej suma wektorowa wszystkich sił i momentów sił działających na to ciało jest równa zero. Z warunki równowagi sił zapisanego dla belki, mamy:

$$\vec{Q} + \vec{F_A} \hspace{.1cm} – \hspace{.1cm} \vec{F_B} = 0 \hspace{1cm} \longrightarrow \hspace{1cm} \vec{Q} + \vec{F_A} = \vec{F_B}$$

Z kolei, z warunku równowagi momentów sił, zapisanego względem punktu A, mamy:

$$\vec{M_Q} + \vec{M_A} \hspace{.1cm} – \hspace{.1cm} \vec{M_B} = 0 \hspace{1cm} \longrightarrow \hspace{1cm} \vec{M_Q} \cdot |AS| + \vec{M_A} \cdot 0 = \vec{M_Q} \cdot |AS| = \vec{M_B} \cdot |AB|$$

Odcinek |AS| ma długość  $\tfrac{1}{2} \hspace{.05cm} l = \tfrac{1}{2} \cdot 3 \hspace{.05cm} \textrm{m} = 1,\hspace{-.05cm}5 \hspace{.05cm} \textrm{m}$ , a odcinek |AB| jest równy 1 m, zatem:

$$Q \cdot 1,\hspace{-.05cm}5 \hspace{.05cm} \textrm{m} = F_B$$

Ciężar belki Q  = 120 N, dlatego też:

$$F_B = 120 \hspace{.05cm} \textrm{N} \cdot 1,\hspace{-.05cm}5 \hspace{.05cm} \textrm{m} = 180 \hspace{.05cm} \textrm{N}$$

Znając wartość siły  $\vec{F_B}$  możemy przystąpić do obliczenia wartości siły  $\vec{F_A}$ :

$$Q + F_A = F_B \hspace{1cm} \longrightarrow \hspace{1cm} F_A = F_B \hspace{.1cm} – \hspace{.1cm} Q = 180 \hspace{.05cm} \textrm{N} \hspace{.1cm} – \hspace{.1cm} 120 \hspace{.05cm} \textrm{N} = 60 \hspace{.05cm} \textrm{N}$$

Prawidłowa odpowiedź: F_A = 60 N, F_B = 180 N.

Zgodnie z teorią wektor natężenia pola elektrycznego w dowolnym punkcie przestrzeni jest zawsze zwrócony od ładunku dodatniego. Aby obliczyć wartość wypadkowego natężenia pola elektrycznego w punkcie A , musimy dodać wektorowo wektory natężenia pola w tym punkcie pochodzące od każdego z tych ładunków. Zwróć uwagę, że zgodnie z powyższym rysunkiem wektory natężenia pola pochodzące od ładunków +Q  (jasnoszare strzałki) wzajemnie się równoważą (jednakowe długości wektorów, lecz przeciwne zwroty), w związku z czym wypadkowy wektor natężenia pola elektrycznego w punkcie A  jest równy wektorowi natężenia pola elektrycznego  $\vec{E}_q$  pochodzącego od ładunku +q :

$$\vec{E}_A = \vec{E}_q = k \frac{q}{r^2}$$

gdzie k  to stała elektrostatyczna, a r  to odległość ładunku +q  od punktu A .

Aby wyrazić odległość r  w oparciu o a , czyli długość boku trójkąta równobocznego, skorzystamy z faktu, że odległość r , dzieląca ładunek q  od punktu A , jest równa wysokości trójkąta równobocznego. Wysokość ta wynosi  $h = \frac{\sqrt{3} \hspace{.05cm} a}{2}$ , dlatego:

$$E_A = k \frac{q}{r^2} = \frac{k \hspace{.05cm} q}{\left( \dfrac{\sqrt{3} \hspace{.05cm} a}{2} \right)^2} = \frac{4 \hspace{.05cm} k \hspace{.05cm} q}{3 \hspace{.05cm} a^2}$$

Prawidłowa odpowiedź: wypadkowe natężenia pola elektrycznego w punkcie A  jest równe  $E_A = \frac{4 \hspace{.05cm} k \hspace{.05cm} q}{3 \hspace{.05cm} a^2}$ .

W zadaniu tym należy zauważyć, że wraz z dwukrotnym zmniejszeniem długości boku trójkąta równobocznego odległość każdego z ładunków od punktu S '  także maleje dwukrotnie. Dla takiej samej konfiguracji oraz wartości ładunków wartość wypadkowego natężenia pola elektrycznego zależy tylko i wyłącznie od odległości dzielącej każdy z ładunków od punktu, w którym to pole chcemy obliczyć. Aby więc sprawdzić jak zmieni się wartość wypadkowego natężenia pola elektrycznego  $\vec{E}_{wyp,S’}$  w punkcie S '  w stosunku do  $\vec{E}_{wyp,S}$  w punkcie S  nie musimy obliczać wartości tego pola dla jednego oraz drugiego przypadku, tylko skorzystać z prostego podstawienia:

$$\dfrac{E_{wyp,S’}}{E_{wyp,S}} = \dfrac{\dfrac{E}{\tfrac{1}{2} \hspace{.05cm} a^2}}{\dfrac{E}{a^2}} = \dfrac{a^2}{\tfrac{1}{4} \hspace{.05cm} a^2} = 4$$

gdzie a  to długość boku trójkąta równobocznego.

Widzimy więc, że wypadkowe natężenia pola elektrycznego wzrośnie czterokrotnie.

Prawidłowa odpowiedź: odpowiedź D.

Rozwiązania kolejnych zadań z tego arkusza maturalnego znajdziesz na poniższych stronach: