Arkusz maturalny z fizyki – poziom rozszerzony – rok 2020 („nowa matura”) – zadania nr 9 – 12

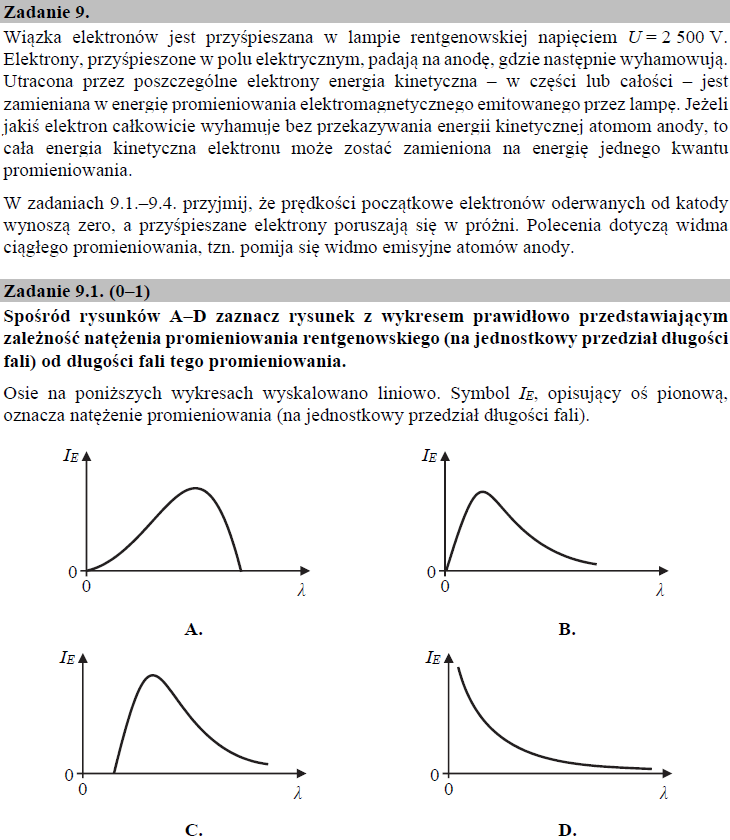
Cechą charakterystyczną ciągłego widma promieniowania rentgenowskiego jest dobrze określona minimalna długość fali (tzw. granica krótkofalowa), poniżej której widmo to zanika (natężenie promieniowania jest równe zero). Granica krótkofalowa ma oczywiście wartość większą od zera, dlatego też prawidłową zależność pomiędzy natężeniem a długością fali promieniowania X przedstawia wykres na rysunku C.

Prawidłowa odpowiedź: rysunek C.

Zdanie 1

Energię fotonu E_f  możemy przedstawić jako:

$$E_f = h \hspace{.05cm} \nu = h \hspace{.05cm} \frac{c}{\lambda}$$

gdzie h  to stała Plancka, c  – prędkość światła w próżni, a λ  – długość fali fotonu.

Po przekształceniu powyższego wzoru względem długości fali λ , mamy:

$$\lambda = \frac{h \hspace{.05cm} c}{E_f}$$

Granica krótkofalowa λ_min  odpowiada zderzeniu, w którym elektron padający na anodę przekazuje podczas pojedynczego zderzenia z atomem materiału anody całą swoją energię kinetyczną E_k . Energię kinetyczną E_k  elektronu, przy założeniu, że jego początkowa prędkość jest równa zero, możemy zapisać jako:

$$ E_k = e \hspace{.05cm} U$$

dlatego, też:

$$\lambda = \lambda_{min} = \frac{h \hspace{.05cm} c}{E_f} = \frac{h \hspace{.05cm} c}{E_k} = \frac{h \hspace{.05cm} c}{e \hspace{.05cm} U}$$

Widzimy więc, że minimalna długość fali promieniowania rentgenowskiego jest odwrotnie proporcjonalna do napięcia przyspieszającego elektrony, a więc zdanie to jest fałszywe.

Zdanie 2

Wraz ze wzrostem napięcia przyspieszającego elektrony wartość minimalnej długości promieniowania rentgenowskiego λ_min  maleje, dlatego też zdanie to jest prawdziwe (zobacz wzór na λ_min ).

Zdanie 3

Zgodnie ze wzorem  $E_f = \frac{h \hspace{.05cm} c}{\lambda}$  energia fotonu, pomijając h  i c , które są stałymi, zależy tylko i wyłącznie od długości fali λ . Wzrost liczby elektronów w wiązce bombardującej anodę przyczynia się do zwiększenia natężenia promieniowania rentgenowskiego, a nie do zwiększenia maksymalnej energii kwantu tegoż promieniowania (długość fali nie ulega zmianie), w związku z czym zdanie to jest zdaniem fałszywym.

Prawidłowa odpowiedź: 1 – F, 2 – P, 3 – F.

Za przyspieszanie elektronów w lampie rentgenowskiej odpowiada pole elektryczne przykładane między katodą a anodą. Pole te wykonuje pracę W  nad elektronami, skutkiem czego elektrony te uzyskują pewną energię kinetyczną E_k . Wiemy, że początkowa prędkość elektronów oderwanych od katody była równa zero, dlatego też możemy zapisać:

$$E_k = W \hspace{1cm} \longrightarrow \hspace{1cm} \tfrac{1}{2} \hspace{.05cm} m_e \hspace{.05cm} V^2 = e \hspace{.05cm} U$$

gdzie m_e , V  i e  o odpowiednio masa, prędkość i ładunek elektronu, a U  to napięcie lampy rentgenowskiej równe 2500 V.

Po przekształceniu powyższego wzoru względem prędkości V , dostaniemy:

$$V^2 = \frac{2 \hspace{.05cm} e \hspace{.05cm} U}{m_e} \hspace{1cm} \longrightarrow \hspace{1cm} V = \sqrt{\frac{2 \hspace{.05cm} e \hspace{.05cm} U}{m_e}}$$

i w konsekwencji:

$$V = \sqrt{\frac{2 \cdot 1,\hspace{-.05cm}6021 \cdot 10^{-19} \hspace{.05cm} \textrm{C} \cdot 2500 \hspace{.05cm} \textrm{V}}{9,\hspace{-.05cm}1031 \cdot 10^{-31} \hspace{.05cm} \textrm{kg}}} \approx 2,\hspace{-.05cm}97 \cdot 10^7 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}} $$

Prawidłowa odpowiedź: prędkość elektronów padających na anodę wynosi ok. 2,97 ⋅ 10⁷ m/s.

Korzystamy ze wzoru na minimalną długość fali promienowania rentgenowskiego (zobacz zadanie 9.1):

$$\lambda_{min} = \frac{h \hspace{.05cm} c}{e \hspace{.05cm} U} = \frac{6,\hspace{-.05cm}6256 \cdot 10^{-34} \hspace{.05cm} \textrm{J} \cdot \textrm{s} \cdot 3 \cdot 10^8 \hspace{.05cm} \frac{\textrm{m}}{\textrm{s}}}{1,\hspace{-.05cm}6021 \cdot 10^{-19} \hspace{.05cm} \textrm{C} \cdot 2500 \hspace{.05cm} \textrm{V}} \approx 4,\hspace{-.05cm}96 \cdot 10^{-10} \hspace{.05cm} \textrm{m}$$

Prawidłowa odpowiedź: najmniejsza długość fali promieniowania rentgenowskiego wytwarzanego przez tą lampę wynosi ok. 4,96 ⋅ 10^-10 m.

Zauważ, że obwód z rysunku 1 i 2 składa się z dwóch głównych gałęzi. Rezystancja górnej gałęzi jest równa R₄ , a rezystancja dolnej gałęzi wynosi  $R_1 + \frac{R_2 \cdot R_3}{R_2 + R_3}$  (mieszane połączenie rezystorów). Ponieważ wiemy, że R₁  = R₂  = R₃  = R₄  = R , dlatego też górna gałąź ma opór równy R , a gałąź dolna  $\frac{3}{2} \hspace{.05cm} R$ . Oznacza to, że przez górną gałąź przepłynie prąd o większym natężeniu niż przez gałąź dolną (górna gałąź mając mniejszy opór w mniejszym stopniu "przeciwstawia się" przepływowi prądu w porównaniu z dolną gałęzią). Dodatkowo, prąd po przepłynięciu przez opornik R₁  i wpłynięciu do węzła za tym rezystorem, ulega kolejnemu "rozdzieleniu". Wówczas I₁  > I₃ , I₁  > I₂  oraz I₂  = I₃ . W związku z powyższym prawidłowe relacje pomiędzy natężeniami prądów w obwodzie z rysunku 1 zawiera odpowiedź B.

Prawidłowa odpowiedź: odpowiedź B.

Gdy klucz K zostanie otwarty rezystancja dolnej gałęzi wzrośnie – prąd nie będzie płynął przez rezystor R₃ , a więc rezystory R₁  i R₂  będziemy mogli traktować jak dwa rezystory połączone szeregowo. Wskutek tego rezystancja dolnej gałęzi nie będzie równa  $\frac{3}{2} \hspace{.05cm} R$ , jak w przykładzie z zadania 10.1, lecz będzie wynosić 2R . W związku z tym natężenie prądu płynącego przez dolną gałąź ulegnie zmniejszeniu, a więc natężenie prądu płynącego przez rezystor R₁  również ulegnie zmniejszeniu. Skoro natężenie I₁  będzie mniejsze, mniejszy będzie również spadek napięcia na tym rezystorze.

Zupełnie z odwrotną sytuacją będziemy mieć do czynienia w przypadku rezystora R₂ . Tutaj natężenie prądu I₂  będzie większe niż w przypadku z rysunku 1 (gdy klucz K był zamknięty wartość natężenia prądu płynącego przez opornik R₂  była równa połowie wartości natężenia prądu I₁ ), w związku z czym spadek napięcia na tym rezystorze także ulegnie zwiększeniu.

W przypadku rezystora R₄  otwarcie klucza K nie spowoduje ani zmiany natężenia prądu, ani spadku napięcia na tym rezystorze, ponieważ rezystancja tego opornika, a więc także i rezystancja górnej gałęzi, pozostaje bez zmian.

Prawidłowa odpowiedź: R₁: I  – zmaleje, U  – zmaleje; R₂: I  – wzrośnie, U  – wzrośnie; R₄: I  – nie zmieni się, U  – nie zmieni się.

Zdanie 1

Rozpad beta minus (β^– ) to proces rozpadu jądra atomowego, podczas którego neutron ulega przemianie w proton (zjawisku temu towarzyszy także emisja elektronu oraz antyneutrina elektronowego). W związku z powyższym podczas każdego procesu rozpadu beta minus liczba neutronów w jądrze atomowym zmniejsza się, a więc zdanie to jest prawdziwe.

Zdanie 2

Protony są nieznacznie cięższe od neutronów, a więc liczba masowa jądra atomowego, wskutek przemiany beta minus, wzrasta. Oznacza to, że zdanie to jest fałszywe.

Zdanie 3

Liczba protonów wskutek rozpadu beta minus wzrasta, a więc zdanie to jest prawdziwe.

Prawidłowa odpowiedź: 1 – P, 2 – F, 3 – P.

Czas połowicznego rozpadu to czas, w którym liczba nietrwałych obiektów (np. nietrwałych izotopów danego pierwiastka) zmniejsza się o połowę. Wyniki pomiarów przedstawione w powyższej tabeli są do siebie bardzo zbliżone w związku z czym czas połowicznego rozpadu tego izotopu musi być dłuższy niż 5 dni.

Prawidłowa odpowiedź: odpowiedź C.

Każdemu rozpadowi beta minus towarzyszy emisja pojedynczego elektronu, w związku z czym liczba zliczeń tychże cząstek przez detektor odpowiada liczbie jąder, które uległy temu rozpadowi. Przy założeniu sferycznie symetrycznego rozkładu promieniowania, o którym mowa w zadaniu (pole powierzchni na jaką padały elektrony zliczane przez detektor stanowiło 1/16 pola sfery), liczba jąder, które uległy rozpadowi podczas pierwszego dnia była równa:

$$\Delta \hspace{.03cm} N = 16 \cdot 1374 \hspace{.05cm} \textrm{rozpadów} = 21984 \hspace{.05cm} \textrm{rozpadów}$$

Znając ilość rozpadów możemy przystąpić do obliczenia średniej aktywności promieniotwórczej A  badanej próbki:

$$A = \frac{\Delta \hspace{.03cm} N}{\Delta \hspace{.03cm} t} = \frac{21984 \hspace{.05cm} \textrm{rozpadów}}{300 \hspace{.05cm} \textrm{s}} \approx 73 \hspace{.05cm} \tfrac{\textrm{rozpadów}}{\textrm{s}} \approx 73 \hspace{.05cm} \textrm{Bq}$$

Prawidłowa odpowiedź: średnia aktywność próbki była równa ok. 73 Bq.

Ruch orbitalny planety Draugr wokół pulsara PSR1257+12 odbywa się pod wpływem działania siły grawitacji występującej między nim a pulsarem. Siła ta pełni rolę siły dośrodkowej. Zapisując drugą zasadę dynamiki Newtona dla tego przypadku, mamy:

$$G \frac{m_p \hspace{.05cm} M_D}{r^2} = M_D \hspace{.05cm} a = M_D \hspace{.05cm} \frac{V^2}{r} \hspace{1cm} \longrightarrow \hspace{1cm} G \frac{m_p}{r^2} = \frac{V^2}{r}$$

gdzie G  to stała grawitacji, m_p  – masa pulsara, M_D  – masa planety Draugr, r  – odległość dzieląca środek pulsara od środka planety Draugr, a V  to prędkość liniowa planety Draugr.

Zakładając, że ruch tej planety po orbicie wokół pulsara odbywa sie ze stałą wartością prędkości V  oraz korzystając ze wzrou na prędkość w ruchu jednostajnym po okręgu ( $V = \frac{2 \hspace{.05cm} \pi \hspace{.05cm} r}{T}$ ), gdzie T  to okres obiegu pulsara przez planetę Draugr, mamy:

$$G \frac{m_p}{r^2} = \frac{V^2}{r} = \frac{4 \hspace{.05cm} \pi^2 \hspace{.05cm} r^2}{T^2 \hspace{.05cm} r} = \frac{4 \hspace{.05cm} \pi^2 \hspace{.05cm} r}{T^2}$$

Po przekształceniu powyższego równania względem masy pulsara m_p , mamy:

$$m_p = \frac{4 \hspace{.05cm} \pi^2 \hspace{.05cm} r^3}{G \hspace{.05cm} T^2}$$

i w konsekwencji:

$$m_p = \frac{4 \cdot \left( 3,\hspace{-.05cm}14 \right)^2 \cdot \left( 0,\hspace{-.05cm}19 \right)^3 \cdot \left( 150 \cdot 10^9 \hspace{.05cm} \textrm{m} \right)^3 }{6,\hspace{-.05cm}67 \cdot 10^{-11} \hspace{.05cm} \tfrac{\textrm{N} \cdot \textrm{m}^2}{\textrm{kg}^2} \cdot \left( 2185920 \hspace{.05cm} \textrm{s} \right)^2} \approx 2,\hspace{-.05cm}9 \cdot 10^{30} \hspace{.05cm} \textrm{kg}$$

Prawidłowa odpowiedź: masa pulsara wynosi w przybliżeniu 2,9 ⋅ 10³⁰ kg.

Aby obliczyć częstotliwość obrotu jądra gwiazdy dookoła własnej osi w chwili, gdy miało ono promień równy 10 R₁ , skorzystamy z zasady zachowania momentu pędu. Zgodnie z treścią zadania możemy pominąć ewentualne straty momentu pędu oraz wpływ innych obiektów na pulsar, w związku z czym możemy założyć, że moment pędu pulsara przed oraz po zmniejszeniu promienia jego jądra przyjmuje stałą wartość:

$$L_{10} = L_1$$

gdzie L₁₀  to moment pędu pulsara o promieniu jądra R₁₀  = 10 R₁ , a L₁  to moment pędu pulsara o promieniu jądra R₁ .

Moment pędu L  wynosi I ω , gdzie I  to moment bezwładności, a ω  to prędkość kątowa obracającego się ciała. Możemy więc zapisać:

$$I_{10} \hspace{.05cm} \omega_{10} = I_1 \hspace{.05cm} \omega_1$$

Wiemy, że moment bezwładności pulsara jest równy kMR² . Prędkość kątowa ω  wynosi 2πf , dlatego:

$$10 \hspace{.05cm} k \hspace{.05cm} M \hspace{.05cm} R_1^2 \cdot 2 \hspace{.05cm} \pi \hspace{.05cm} f_{10} = k \hspace{.05cm} M \hspace{.05cm} R_1^2 \cdot 2 \hspace{.05cm} \pi \hspace{.05cm} f_1$$

skąd po skróceniu, otrzymamy:

$$100 \hspace{.05cm} f_{10} = f_1$$

Wiemy, że f₁  = 160 Hz, dlatego też:

$$f_{10} = \frac{f_1}{100} = \frac{160 \hspace{.05cm} \textrm{Hz}}{100} = 1,\hspace{-.05cm}6 \hspace{.05cm} \textrm{Hz}$$

Prawidłowa odpowiedź: częstotliwość obrotu jądra gwiazdy wokół własnej osi wynosi 1,6 Hz.

Energia kinetyczna pulsara obracającego się wokół własnej osi wynosi:

$$E_k = \tfrac{1}{2} \hspace{.05cm} I \hspace{.05cm} \omega^2$$

Korzystając z oznaczeń oraz wzorów na I  i ω  dla obydwu przypadków, mamy:

$$E_{k10} = \tfrac{1}{2} \hspace{.05cm} I_{10} \hspace{.05cm} \omega_{10}^2 = \tfrac{1}{2} \hspace{.05cm} k \hspace{.05cm} M \hspace{.05cm} R_{10}^2 \cdot \left( 2 \hspace{.05cm} \pi \hspace{.05cm} f_{10} \right)^2 = 200 \hspace{.05cm} k \hspace{.05cm} M \hspace{.05cm} R_1^2 \hspace{.05cm} \pi^2 \hspace{.05cm} f_{10}^2$$

oraz:

$$E_{k1} = \tfrac{1}{2} \hspace{.05cm} I_{1} \hspace{.05cm} \omega_{1}^2 = \tfrac{1}{2} \hspace{.05cm} k \hspace{.05cm} M \hspace{.05cm} R_{1}^2 \cdot \left( 2 \hspace{.05cm} \pi \hspace{.05cm} f_{1} \right)^2 = 2 \hspace{.05cm} k \hspace{.05cm} M \hspace{.05cm} R_1^2 \hspace{.05cm} \pi^2 \hspace{.05cm} f_{1}^2$$

Podstawiajac powyższe wyrażenia do wzrou  $\dfrac{E_{k1}}{E_{k10}}$ , dostaniemy:

$$\frac{E_{k1}}{E_{k10}} = \frac{2 \hspace{.05cm} k \hspace{.05cm} M \hspace{.05cm} R_1^2 \hspace{.05cm} \pi^2 \hspace{.05cm} f_{1}^2}{200 \hspace{.05cm} k \hspace{.05cm} M \hspace{.05cm} R_1^2 \hspace{.05cm} \pi^2 \hspace{.05cm} f_{10}^2} = \frac{f_1^2}{100 \hspace{.05cm} f_{10}^2}$$

Częstotliwość f₁  oraz f₁₀  jest znana, a więc:

$$\frac{E_{k1}}{E_{k10}} = \frac{\left( 160 \hspace{.05cm} \textrm{Hz} \right)^2}{100 \cdot \left( 1,\hspace{-.05cm}6 \hspace{.05cm} \textrm{Hz} \right)^2} = 100$$

Prawidłowa odpowiedź: szukany stosunek energii kinetycznych jest równy 100.

Rozwiązania kolejnych zadań z tego arkusza maturalnego znajdziesz na poniższych stronach: