Arkusz maturalny z fizyki – poziom rozszerzony – rok 2019 („nowa matura”) – zadania nr 1 – 4

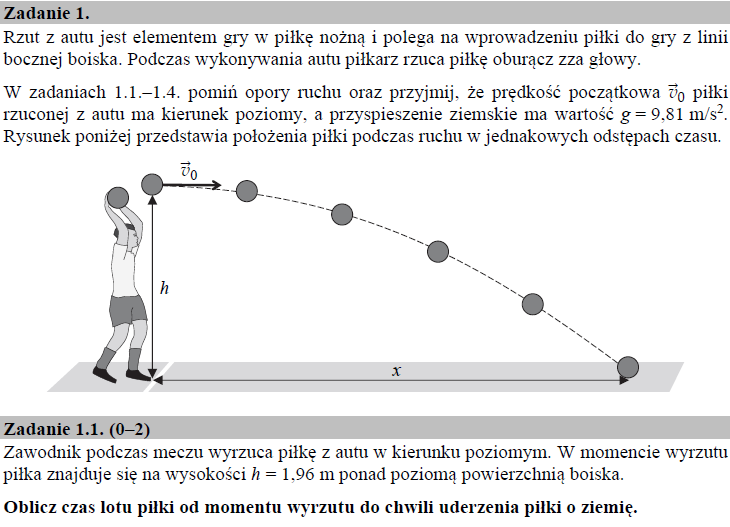
Wyrzut piłki z autu to przykład rzutu poziomego. Rzut poziomy traktowany jest jako złożenie dwóch ruchów: ruchu jednostajnego prostoliniowego odbywającego się w kierunku poziomym oraz spadku swobodnego odbywającego się w kierunku pionowym. Podczas ruchu w kierunku poziomym ciało porusza się ze stałą wartością prędkości (zobacz: ruch jednostajny prostoliniowy), a podczas spadku swobodnego – ze stałą wartością przyspieszenia, równą przyspieszeniu ziemskiemu g. Podczas spadku swobodnego prędkość ciała wzrasta w sposób liniowy, a sam wektor prędkości zwrócony jest w stroną podłoża. Aby więc obliczyć czas lotu piłki od momentu jej wyrzutu z wysokości h  do momentu uderzenia o podłoże, skorzystamy z faktu, że czas ten odpowiada czasowi trwania spadku swobodnego z wysokości h. Z równania opisującego drogę w ruchu jednostajnie przyspieszonym, zapisanego dla spadku swobodnego, dostaniemy:

$$y = V_0 \hspace{.05cm} t \hspace{.15cm} – \hspace{.1cm} \dfrac{g \hspace{.05cm} t^2}{2} + y_0$$

gdzie y  to położenie ciała (wysokość) w chwili t , V₀  – początkowa prędkość ciała, g – przyspieszenie ziemskie, a y₀  to początkowa wysokość ciała.

W chwili wyrzutu początkowa prędkość piłki w kierunku pionowym jest równa 0 m/s (prędkość początkowa piłki ma kierunek poziomy), a y₀  = h  = 1,96 m. Gdy piłka uderza o podłoże wysokość y  = 0 m, zatem:

$$0 = 0 \cdot t \hspace{.15cm} – \hspace{.1cm} \dfrac{g \hspace{.05cm} t^2}{2} + h \hspace{1cm} \longrightarrow \hspace{1cm} h = \dfrac{g \hspace{.05cm} t^2}{2} \hspace{1cm} \longrightarrow \hspace{1cm} t = \sqrt{\dfrac{2 \hspace{.05cm} h}{g}}$$

Po podstawieniu do powyższego wzoru wartości liczbowych oraz wykonaniu obliczeń, otrzymamy:

$$t = \sqrt{\dfrac{2 \cdot 1,\hspace{-.05cm}96 \hspace{.05cm} \textrm{m}}{9,\hspace{-.05cm}81 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2}}} = 0,\hspace{-.05cm}63 \hspace{.05cm} \textrm{s}$$

Prawidłowa odpowiedź: czas lotu piłki t  = 0,63 s.

Ruch piłki w kierunku poziomym odpowiada ruchowi jednostajnie prostoliniowemu, w związku z czym odległość x  przebytą przez piłkę w kierunku poziomym opisuje wzór na drogę w tym właśnie ruchu:

$$x = V \hspace{.05cm} t$$

Prędkość w ruchu jednostajnym prostoliniowym nie ulega zmianie w funkcji czasu. Wiemy, że w chwili wyrzutu prędkość piłki była równa V₀  i miała kierunek poziomy (brak składowej pionowej prędkości), w związku z czym prędkość V, z jaką piłka poruszała się w poziomie była równa początkowej prędkości piłki (V  = V₀ ). Wiemy także, że piłka spadła na boisko w odległości 5,1 m od miejsca jej wyrzutu. Czas lotu piłki znamy, bo wyznaczyliśmy go w zadaniu 1.1, dlatego też:

$$x = V_0 \cdot \sqrt{\dfrac{2 \hspace{.05cm} h}{g}} \hspace{1cm} \longrightarrow \hspace{1cm} V_0 = \dfrac{x}{\sqrt{\dfrac{2 \hspace{.05cm} h}{g}}} = \dfrac{5,\hspace{-.05cm}1 \hspace{.05cm} \textrm{m}}{0,\hspace{-.05cm}63 \hspace{.05cm} \textrm{s}} = 8,\hspace{-.05cm}1 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}}$$

Prawidłowa odpowiedź: prędkość początkowa piłki była równa 8,1 m/s.

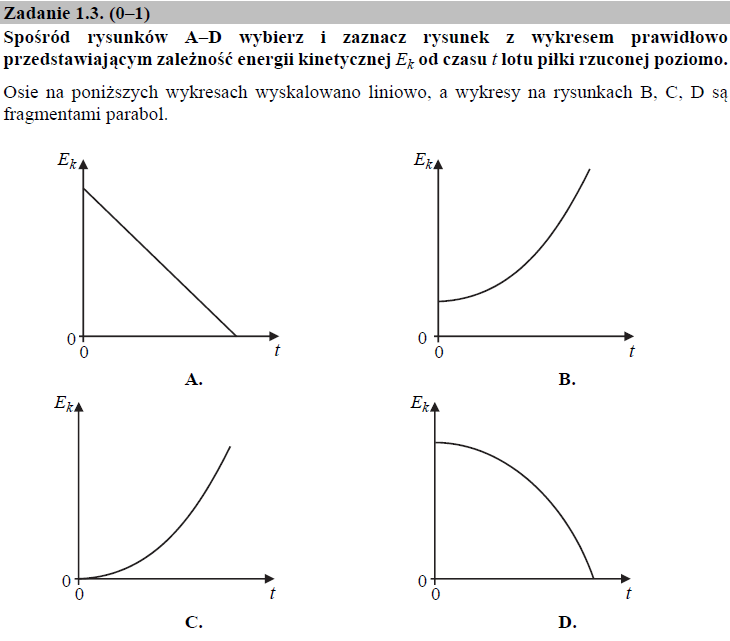
Piłka na początku ruchu miała pewną prędkość początkową, w związku z czym jej początkowa energia kinetyczna również była różna od zera. Wraz z upływem czasu, prędkość piłki wzrastała, ponieważ jej składowa pionowa prędkości stopniowo zwiększała swoją wartość. Ponieważ energia kinetyczna jest wprost proporcjonalna do kwadratu prędkości ciała, dlatego też szukamy wykresu, w którym zależność energii kinetycznej od czasu reprezentowana jest przez krzywą rosnącą, będącą fragmentem paraboli, która to dodatkowo w chwili t  = 0 s posiada pewną, niezerową wartość. Powyższe warunki spełnia tylko wykres B.

Prawidłowa odpowiedź: wykres B.

Obydwie piłki zostały upuszczone (zrzucone) z tej samej wysokości, a więc zgodnie z odpowiedzią na pytanie 1.1, czas lotu tychże piłek będzie jednakowy. Aby odpowiedzieć na drugą część tego pytania należy zauważyć, że w przypadku rzutu poziomego wektor prędkości $\vec{V}$ posiada dwie składowe: składową poziomą oraz pionową, podczas, gdy wektor prędkości ciała spadającego swobodnie posiada tylko składową pionową. Dla obydwu tych przypadków składowe pionowe prędkości są sobie równe, w związku z czym większą prędkość tuż przed uderzeniem o podłoże będzie posiadać piłka P₁ (wypadkowa prędkość piłki P₁ jest równa sumie jej dwóch składowych).

Prawidłowa odpowiedź: A – 2.

Powiedzenie punkt widzenia zależy od punktu siedzenia  idealnie pasuje do tego zadania. Kabina spada swobodnie z przyspieszeniem a = g. Konsekwencją tego ruchu jest ‘pojawienie się’ w kabinie sił bezwładności działających na znajdujące się w niej obiekty. Siła bezwładności to pozorna siła działająca na ciało znajdujące się w układzie nieinercjalnym, spowodowana przyspieszeniem tego układu (kabina porusza się z przyspieszeniem, a więc należy ją traktować jako układ nieinercjalny). Siła bezwładności ma wartość – m a, gdzie m  to masa ciała, a a – przyspieszenie ciała (układu). Ponieważ, jak napisaliśmy wyżej, kabina porusza się z przyspieszeniem a = g, w związku z czym siła bezwładności działająca na piłkarza oraz wyrzuconą przez niego piłkę będzie wynosić – m g, a więc będzie równa sile ciężkości ze znakiem minus. Wiemy, że piłkarz wyrzucił piłkę z prędkością początkową V₀, skierowaną równolegle do podłogi kabiny. Pod nieobecność oporów powietrza prędkość tej piłki nie ulegnie więc zmianie. Dodatkowo, ze względu na równoważenie się siły ciężkości oraz siły bezwładności, tor ruchu piłki także nie ulegnie zmianie, a więc będzie się ona poruszać równolegle do powierzchni podłogi kabiny.

Prawidłowa odpowiedź: odpowiedź A.

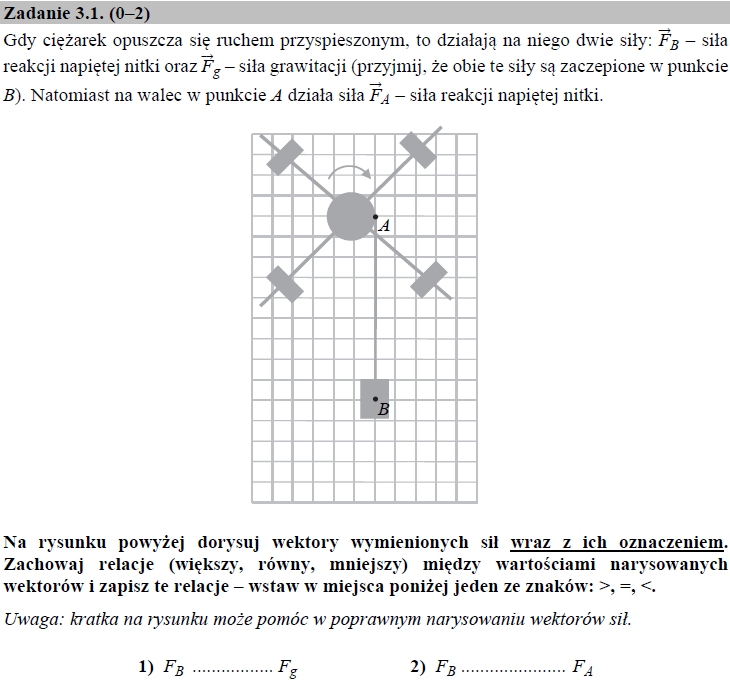
Aby ciężarek mógł poruszać się ruchem przyspieszonym (siła wypadkowa większa od zera), siła ciężkości $\vec{F_g}$  musi mieć większą wartość, niż siła reakcji napiętej nitki $\vec{F_B}$. Ruch obrotowy walca zachodzi pod wpływem momentu siły, którego źródłem jest siła reakcji napiętej nici $\vec{F_A}$. Zgodnie z trzecią zasadą dynamiki Newtona wartość tej siły musi odpowiadać wartości siły $\vec{F_B}$ , a więc $\vec{F_A} = \vec{F_B}$.

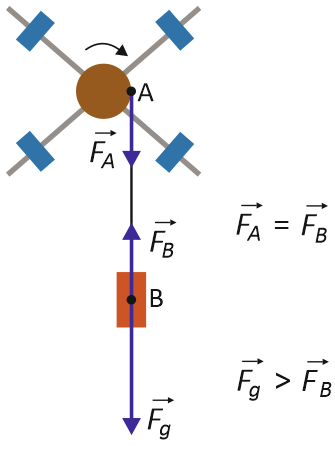
Prawidłowa odpowiedź: $\vec{F_B} < \vec{F_g}$ , $\vec{F_B} = \vec{F_A}$.

Ciężarek porusza się w kierunku pionowym ze stałym przyspieszeniem a, dlatego aby obliczyć wartość tego przyspieszenia skorzystamy z równania na drogę w ruchu jednostajnie przyspieszonym, zapisanym dla spadku swobodnego ciała:

$$y = V_0 \hspace{.05cm} t \hspace{.15cm} – \hspace{.1cm} \dfrac{a \hspace{.05cm} t^2}{2} + y_0$$

gdzie y  to położenie ciężarka w chwili t , V₀  – początkowa prędkość ciężarka, a – przyspieszenie opadającego ciężarka, a y₀  to początkowa wysokość ciężarka.

Początkowa prędkość ciężarka była równa zero, dlatego V₀  = 0 m/s. Położenie ciężarka y  po czasie t = 1,6 s, a więc po jego upadku na podłoże, wynosi y = 0 m, z kolei y₀  odpowiada wysokości h = 0,96 m. Mamy więc:

$$0 = 0 \cdot t \hspace{.15cm} – \hspace{.1cm} \dfrac{a \hspace{.05cm} t^2}{2} + h \hspace{1cm} \longrightarrow \hspace{1cm} h = \dfrac{a \hspace{.05cm} t^2}{2} \hspace{1cm} \longrightarrow \hspace{1cm} a = \dfrac{2 \hspace{.05cm} h}{t^2}$$

Wartość h  oraz t  jest znana, w związku z czym:

$$a = \dfrac{2 \cdot 0,\hspace{-.05cm}960 \hspace{.05cm} \textrm{m}}{\left( 1,\hspace{-.05cm}6 \hspace{.05cm} \textrm{s} \right)^2} = 0,\hspace{-.05cm}750 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2}$$

(wysokość zmierzono z dokładnością do trzech miejsc po przecinku, dlatego wartość liczbową przyspieszenia zapisaliśmy z taką samą dokładnością)

Prawidłowa odpowiedź: przyspieszenie spadającego ciężarka było równe 0,750 m/s².

Podpunkt b)

W miejsce funkcji f (x ) wstawiamy zależność na przyspieszenie występującą w zadaniu 3.2 tj. (2 h)/t². W tym przypadku zakładamy, że pomiar czasu był dokładny, a pomiar wysokości h  był wykonany z niepewnością Δh  = 5 mm. Mamy więc:

$$\Delta \hspace{.05cm} a_h = \dfrac{1}{2} \cdot \left| \dfrac{2 \left(h + \Delta \hspace{.02cm} h \right)}{t^2} \hspace{.15cm} – \hspace{.1cm} \dfrac{2 \left(h \hspace{.15cm} – \hspace{.1cm} \Delta \hspace{.02cm} h \right)}{t^2} \right| = \dfrac{2 \hspace{.05cm} \Delta \hspace{.02cm} h}{t^2} = \dfrac{2 \cdot 5 \cdot 10^{-3} \hspace{.05cm} \textrm{m}}{\left( 1,\hspace{-.05cm}6 \hspace{.05cm} \textrm{s} \right)^2} \approx 0,\hspace{-.05cm}004 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2}$$

Prawidłowa odpowiedź: niepewność wyznaczenia przyspieszenia a_h  wynosi w przybliżeniu 0,004 m/s².

Podpunkt c)

W tym przypadku zakładamy, że pomiar wysokości był dokładny, a pomiar czasu t  był wykonany z niepewnością Δt  = 0,1 s. Mamy więc:

$$\Delta \hspace{.05cm} a_t = \dfrac{1}{2} \cdot \left| \dfrac{2 \hspace{.05cm} h}{\left( t + \Delta \hspace{.02cm} t \right)^2} \hspace{.15cm} – \hspace{.1cm} \dfrac{2 \hspace{.05cm} h}{\left( t \hspace{.15cm} – \hspace{.1cm} \Delta \hspace{.02cm} t \right)^2} \right| = \left| \dfrac{0,\hspace{-.05cm}960 \hspace{.05cm} \textrm{m}}{\left( 1,\hspace{-.05cm}7 \hspace{.05cm} \textrm{s} \right)^2} \hspace{.15cm} – \hspace{.1cm} \dfrac{0,\hspace{-.05cm}960 \hspace{.05cm} \textrm{m}}{\left( 1,\hspace{-.05cm}5 \hspace{.05cm} \textrm{s} \right)^2} \right| \approx 0,\hspace{-.05cm}1 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2}$$

(w tym przypadku łatwiej podstawić wszystkie wartości liczbowe bezpośrednio do wzoru)

Prawidłowa odpowiedź: niepewność wyznaczenia przyspieszenia a_t  wynosi w przybliżeniu 0,1 m/s².

Podpunkt d)

Na podstawie wyników uzyskanych w podpunktach b) oraz c) możemy stwierdzić, że większy wpływ na niepewność wyznaczenia przyspieszenia miała niepewność wyznaczenia czasu spadającego ciężarka, ponieważ Δa_t  > Δa_h  (stosunek tych dwóch wielkości tj. Δa_t  / Δa_h  wynosi w przybliżeniu 25, a więc o tyle razy wkład niepewności pomiaru czasu na wynik eksperymentu jest większy od wkładu niepewności pomiaru wysokości).

Prawidłowa odpowiedź: większy wpływ na niepewność wyznaczenia przyspieszenia miała niepewność wyznaczenia czasu.

Korzystamy z zasady zachowania energii mechanicznej, którą zapiszemy zarówno dla ciężarka, jak i dla wahadła traktowanego jako całość tj. z uwzględnieniem walca oraz wszystkich czterech prętów i obciążników. Dostaniemy:

$$E_{kp,c} + E_{pp,c} + E_{kp,w} + E_{pp,w} = E_{kk,c} + E_{pk,c} + E_{kk,w} + E_{pk,w}$$

gdzie E_kp,c  i E_pp,c  oraz E_kp,w  i E_pp,w  to początkowa energia kinetyczna i potencjalna odpowiednio ciężarka (indeks dolny ‘c’ ) oraz wahadła (indeks dolny ‘w’ ), a E_kk,c  i E_pk,c  oraz E_kk,w  i E_pk,w  to końcowa energia kinetyczna i potencjalna odpowiednio ciężarka oraz wahadła.

Lewa strona tego równania opisuje energię mechaniczną ciężarka i wahadła w chwili, w której ciężarek i wahadło spoczywają nieruchomo, a prawa strona – w chwili, w której ciężarek uderza o podłoże, a wahadło obraca się wokół własnej osi symetrii. W związku z powyższym możemy zapisać, że początkowa energia kinetyczna ciężarka i wahadła jest równa 0 J (ciała te spoczywają) oraz, że końcowa energia potencjalna ciężarka również wynosi 0 J (ciężarek uderza o podłoże, a więc jego wysokość jest równa 0 m):

$$0 + E_{pp,c} + 0 + E_{pp,w} = E_{kk,c} + 0 + E_{kk,w} + E_{pk,w} \hspace{1cm} \longrightarrow \hspace{1cm} E_{pp,c} + E_{pp,w} = E_{kk,c} + E_{kk,w} + E_{pk,w}$$

Wzór nam się trochę uprościł, więc możemy już podstawić do niego odpowiednie zależności:

$$m \hspace{.05cm} g \hspace{.05cm} h + M \hspace{.05cm} g \hspace{.05cm} H = \dfrac{m \hspace{.05cm} V^2}{2} + \dfrac{I \hspace{.05cm} \omega^2}{2} + M \hspace{.05cm} g \hspace{.05cm} H$$

gdzie m  to masa ciężarka, g  – przyspieszenie ziemskie, h  – wysokość ciężarka w początkowej fazie ruchu, M  – masa wahadła, H  – wysokość środka masy wahadła, I  – moment bezwładności obracającej się części wahadła, a ω  to prędkość kątowa wahadła.

Po skróceniu wyrazów podobnych oraz przekształceniu powyższego wyrażenia względem momentu bezwładności I, dostaniemy:

$$I = \dfrac{2 \hspace{.05cm} m \hspace{.05cm} g \hspace{.05cm} h \hspace{.15cm} – \hspace{.1cm} m \hspace{.05cm} V^2}{\omega^2} = \dfrac{m \left( 2 \hspace{.05cm} g \hspace{.05cm} h \hspace{.15cm} – \hspace{.1cm} V^2 \right)}{\omega^2}$$

Z zadania 3.2 wiemy, że wysokość h  wynosi $\dfrac{a \hspace{.03cm} t^2}{2}$. Prędkość ciężarka w chwili upadku jest równa $V = a \hspace{.05cm} t$ , a prędkość kątowa $w = \dfrac{V}{r}$. W związku z tym, mamy:

$$I = \dfrac{m \left( 2 \hspace{.05cm} g \cdot \dfrac{a \hspace{.05cm} t^2}{2} \hspace{.15cm} – \hspace{.1cm} V^2 \right)}{\dfrac{V^2}{r^2}} = m \hspace{.05cm} r^2 \left( \dfrac{g \hspace{.05cm} a \hspace{.05cm} t^2}{V^2} \hspace{.15cm} – \hspace{.1cm} \dfrac{V^2}{V^2} \right) = m \hspace{.05cm} r^2 \left( \dfrac{g \hspace{.05cm} a \hspace{.05cm} t^2}{a^2 \hspace{.05cm} t^2} \hspace{.15cm} – \hspace{.1cm} 1 \right) = m \hspace{.05cm} r^2 \left( \dfrac{g}{a} \hspace{.15cm} – \hspace{.1cm} 1 \right)$$

Zdanie 1

Moment bezwładności ciała to wielkość fizyczna informująca o tym, jak rozłożona jest masa obracającego się ciała wokół osi jego obrotu. Wartość momentu bezwładności zależy od wyboru osi obrotu oraz od kształtu i rozmieszczenia masy wewnątrz danego ciała. Zamocowanie układu obciążników bliżej osi obrotu walca wpłynie na zmniejszenie ich momentu bezwładności, ponieważ oprócz zmniejszenia odległości tychże obciążników od osi obrotu walca wpływamy również na zmianę rozkładu ich masy (masa obciążników będzie skupiona bliżej osi obrotu, w związku z czym wprawienie wahadła w ruch obrotowy będzie wymagało przyłożenia dużo mniejszej siły).

Zdanie 2

Źródłem momentu siły, powodującego ruch obrotowy walca, jest siła reakcji napiętej nici $\vec{F_A}$. Zgodnie z drugą zasadą dynamiki Newtona, zapisaną dla tego układu, mamy:

$$\vec{M}_{wyp} = I \hspace{.05cm} \vec{\varepsilon} \hspace{1cm} \longrightarrow \hspace{1cm} \vec{r} \times \vec{F_A} = I \hspace{.05cm} \vec{\varepsilon}$$

Widzimy więc, że gdy zmniejszymy moment bezwładności układu obciążników, siła napięcia nitki również zmaleje.

Prawidłowa odpowiedź: 1 – zmalał, 2 – zmalała.

W jednym oraz w drugim przypadku położenie chwilowe pręta, zamocowanego na sprężynach, zawsze było poziome. Oznacza to, że w każdym z tych układów wychylenie sprężyn z położenia równowagi zawsze zmieniało się o taką samą wartość, w związku z czym możemy założyć, że wszystkie te sprężyny posiadały jednakowy współczynnik sprężystości k. Aby obliczyć stosunek częstotliwości drgań pierwszego oraz drugiego układu sprężyn musimy na początek wyznaczyć ich zastępczy współczynnik sprężystości. Wypadkowa siła działająca na pręt jest równa sumie sił sprężystości działających na każdą sprężynę, w związku z czym możemy zapisać (zakładamy, że drgania zachodzą wzdłuż pionowej osi y ):

– pierwszy układ – trzy sprężyny:

$$\vec{F}_{wyp,1} = \hspace{.15cm} – \hspace{.1cm} \left( k \hspace{.05cm} \vec{y} + k \hspace{.05cm} \vec{y} + k \hspace{.05cm} \vec{y} \right) = \hspace{.15cm} – \hspace{.1cm} 3 \hspace{.05cm} k \hspace{.05cm} \vec{y}$$

– drugi układ – dwie sprężyny:

$$\vec{F}_{wyp,2} = \hspace{.15cm} – \hspace{.1cm} \left( k \hspace{.05cm} \vec{y} + k \hspace{.05cm} \vec{y} \right) = \hspace{.15cm} – \hspace{.1cm} 2 \hspace{.05cm} k \hspace{.05cm} \vec{y}$$

Z dwóch powyższych równań ‘wyłania się’ zastępczy współczynnik sprężystości dla obydwu układów. Dla pierwszego układu współczynnik ten wynosi $k_1 = 3 \hspace{.03cm} k$ , a dla drugiego: $k_2 = 2 \hspace{.03cm} k$ . Współczynnik sprężystości k  możemy zapisać jako (zobacz: Siła w ruchu harmonicznym):

$$k = m \hspace{.05cm} \omega^2 = m \hspace{.05cm} \left( 2 \hspace{.05cm} \pi \hspace{.05cm} f \right)^2 = 4 \hspace{.05cm} \pi^2 \hspace{.05cm} f^2 \hspace{.05cm} m$$

Po przekształceniu powyższego wyrażenia względem f, otrzymamy wzór na częstotliwość drgań pierwszego i drugiego układu:

$$f_1^2 = \dfrac{k_1}{4 \hspace{.05cm} \pi^2 \hspace{.05cm} m} = \dfrac{3 \hspace{.05cm} k}{4 \hspace{.05cm} \pi^2 \hspace{.05cm} m} \hspace{1cm} , \hspace{1cm} f_2^2 = \dfrac{k_2}{4 \hspace{.05cm} \pi^2 \hspace{.05cm} m} = \dfrac{2 \hspace{.05cm} k}{4 \hspace{.05cm} \pi^2 \hspace{.05cm} m} = \dfrac{k}{2 \hspace{.05cm} \pi^2 \hspace{.05cm} m}$$

Stosunek częstotliwości drgań f₁ /f₂  jest wobec tego równy:

$$\dfrac{f_1^2}{f_2^2} = \dfrac{\dfrac{3 \hspace{.05cm} k}{4 \hspace{.05cm} \pi^2 \hspace{.05cm} m}}{\dfrac{k}{2 \hspace{.05cm} \pi^2 \hspace{.05cm} m}} = \dfrac{3}{2} \hspace{1cm} \longrightarrow \hspace{1cm} \dfrac{f_1}{f_2} = \sqrt{\dfrac{3}{2}} \approx 1,\hspace{-.05cm}225$$

Prawidłowa odpowiedź: stosunek częstotliwości drgań dla tych dwóch układów sprężyn jest równy w przybliżeniu 1,225.

Rozwiązania kolejnych zadań z tego arkusza maturalnego znajdziesz na poniższych stronach: