Arkusz maturalny z fizyki – poziom rozszerzony – rok 2019 („nowa matura”) – zadania nr 9 – 12

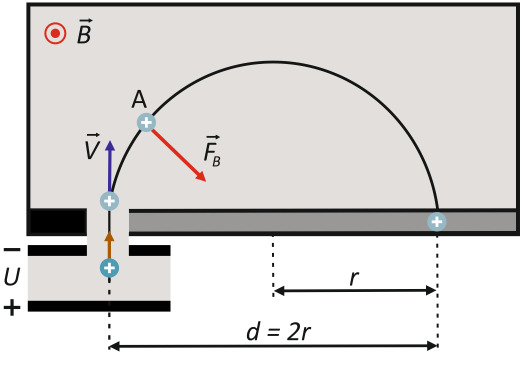
jon dodatni w polu magnetycznym - rysunek schematyczny - nowa matura 2019 - zadanie nr 9_1

Siłą dośrodkową działającą na jon dodatni jest siła Lorentza $\vec{F_B}$, pod wpływem której jon doznaje przyspieszenia dośrodkowego. Druga zasada dynamiki Newtona zapisana dla tego przypadku, wynosi:

$$\vec{F}_{wyp} = \vec{F_B} = m \hspace{.05cm} \vec{a} \hspace{.1cm} \longrightarrow \hspace{1cm} q \hspace{.1cm} V \hspace{.05cm} B = \dfrac{m \hspace{.05cm} V^2}{r}$$

gdzie q to ładunek jonu dodatniego, V – prędkość jonu, B – indukcja pola magnetycznego, a r to promień okręgu, po którym porusza się jon dodatni.

Wiemy, że początkowo spoczywający jon dodatni ulegał przyspieszaniu w polu elektrycznym napięciem U. Zmiana energii kinetycznej jonu odpowiada wartości pracy wykonanej nad jonem przez siły elektryczne. Z porównania tych dwóch wielkości, dostaniemy (pomijamy początkową energię kinetyczną jonu, ponieważ jej wartość wynosi 0 J):

$$\Delta \hspace{.02cm} E_k = W \hspace{1cm} \longrightarrow \hspace{1cm} \tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} V^2 = q \hspace{.1cm} U$$

Ładunek jonu dodatniego wynosi +e , gdzie e to ładunek elementarny. Promień okręgu r jest z kolei równy d/2. Po uwzględnieniu tych wielkości i przekształceniu pierwszego równania względem prędkości V, otrzymamy:

$$e \hspace{.1cm} V \hspace{.05cm} B = \dfrac{m \hspace{.05cm} V^2}{\tfrac{d}{2}} \hspace{1cm} \longrightarrow \hspace{1cm} V = \dfrac{e \hspace{.05cm} B \hspace{.05cm} d}{2 \hspace{.05cm} m}$$

Po wstawieniu powyższego wyrażenia do równania $\tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} V^2 = e \hspace{.05cm} U$, dostaniemy:

$$\tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} \left( \dfrac{e \hspace{.05cm} B \hspace{.05cm} d}{2 \hspace{.05cm} m} \right)^2 = e \hspace{.05cm} U \hspace{1cm} \longrightarrow \hspace{1cm} \tfrac{1}{2} \hspace{.05cm} m \cdot \dfrac{e^2 \hspace{.05cm} B^2 \hspace{.05cm} d^2}{4 \hspace{.05cm} m^2} = \dfrac{e^2 \hspace{.05cm} B^2 \hspace{.05cm} d^2}{8 \hspace{.05cm} m} = e \hspace{.05cm} U$$

i w efekcie:

$$m = \dfrac{e \hspace{.05cm} B^2 \hspace{.05cm} d^2}{8 \hspace{.1cm} U}$$

Prawidłowa odpowiedź: wzór pozwalający obliczyć masę m jonu dodatniego wynosi $\hspace{.1cm} m = \dfrac{e \hspace{.05cm} B^2 \hspace{.05cm} d^2}{8 \hspace{.1cm} U}$.

Prawidłowa odpowiedź: odpowiedź D.

Zdanie 1

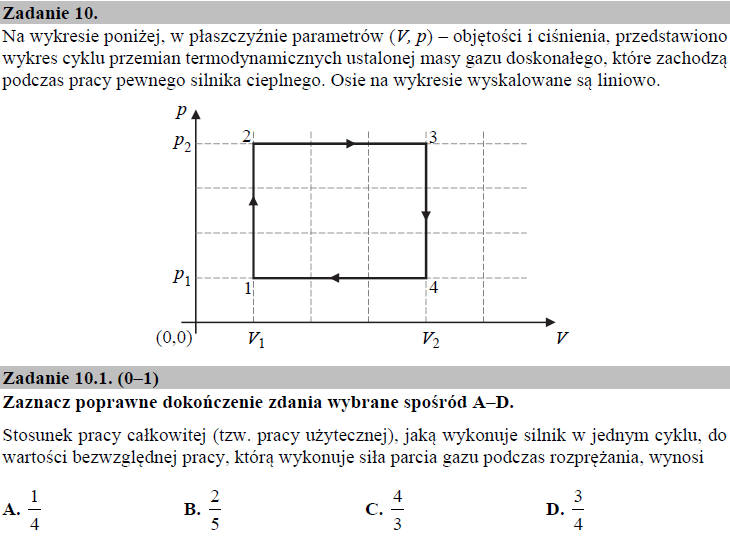
Przemiany 1-2 i 3-4 to przemiany izochoryczne, czyli przemiany zachodzące przy stałej wartości objętości. Podczas tej przemiany układ może wymieniać energię z otoczeniem tylko i wyłącznie wskutek cieplnego przepływu energii (praca nie jest wykonywana). Zmiana ciśnienia gazu jest wprost proporcjonalna do zmiany jego temperatury tj. wraz ze wzrostem ciśnienia, wzrasta również temperatura i odwrotnie. Gdy zmiana ciśnienia (a więc także i temperatury) jest dodatnia mówimy, że układ pobiera ciepło, z kolei gdy zmiana ciśnienia jest ujemna, mówimy, że układ oddaje ciepło. Zgodnie z wykresem p (V ) podczas przemiany 1-2 układ pobierał ciepło (wzrost ciśnienia), a podczas przemiany 3-4 – oddawał je do otoczenia (spadek ciśnienia), w związku z czym zdanie to jest fałszywe.

Zdanie 2

Przemiany 2-3 i 4-1 to przemiany izobaryczne, czyli przemiany zachodzące przy stałej wartości ciśnienia. Wzór pozwalający obliczyć pracę wykonaną przez siły podczas przemiany izobarycznej wynosi:

$$W = p \hspace{.05cm} \Delta \hspace{.02cm} V$$

gdzie p to ciśnienie gazu, a ΔV to zmiana objętości gazu przy zadanym ciśnieniu p.

W zadaniu tym interesuje nas porównanie wartości bezwzględnej pracy dla obydwu tych przemian, dlatego też powyższe wyrażenie możemy zapisać jako:

$$W = p \hspace{.05cm} |\Delta \hspace{.02cm} V|$$

Zgodnie z wykresem p (V ) zmiana objętości gazu w przemianie 2-3 oraz 4-1 przyjmuje, bez uwzględniania znaków, jednakową wartość, dlatego też:

$$W_{2-3} = p_2 \hspace{.05cm} |V_2 \hspace{.15cm} – \hspace{.1cm} V_1| = p_2 \hspace{.05cm} \Delta \hspace{.02cm} V$$

a dla przemiany 4-1:

$$W_{4-1} = p_1 \hspace{.05cm} |V_1 \hspace{.15cm} – \hspace{.1cm} V_2| = p_1 \hspace{.05cm} \Delta \hspace{.02cm} V$$

Ponieważ p₂ > p₁ , dlatego też W_2-3 > W_4-1 , co oznacza, że zdanie to jest fałszywe.

Zdanie 3

Cykl przemian termodynamicznych przedstawiony w tym zadaniu jest cyklem zamkniętym (układ, po wykonaniu przemian powraca na początek cyklu). Cechą charakterystyczną cyklu zamkniętego jest to, że po ‘przejściu’ całego cyklu przemian energia wewnętrzna układu nie ulega zmianie (różnica energii wewnętrznej przed i po wykonaniu pełnego cyklu jest równa zero), w związku z czym zdanie to jest prawdziwe.

Prawidłowa odpowiedź: 1 – F, 2 – F, 3 – P.

Dla cyklu zamkniętego, o którym mowa jest w tym zadaniu, zmiana energii wewnętrznej układu wynosi zero. Oznacza to, że całkowita praca W wykonana podczas jednego, pełnego cyklu pracy tego silnika równa się ciepłu pobranemu Q_pob i oddanemu Q_od przez silnik, co możemy zapisać jako:

$$W = Q_{pob} \hspace{.15cm} – \hspace{.1cm} Q_{od}$$

Aby powiązać ze sobą powyższe wielkości fizyczne skorzystamy z definicji sprawności η silnika cieplnego:

$$\eta = \dfrac{W}{Q_{pob}}$$

Po przekształceniu pierwszego równania względem ciepła pobranego Q_pob i następnie podstawieniu go do równania opisującego sprawność silnika cieplnego, dostaniemy:

$$\eta = \dfrac{W}{Q_{pob}} = \dfrac{W}{W + Q_{od}}$$

Przekształcając następnie powyższe wyrażenie względem ciepła Q_od , otrzymamy:

$$Q_{od} = \dfrac{W}{\eta} \hspace{.15cm} – \hspace{.1cm} W = W \left( \dfrac{1}{\eta} \hspace{.15cm} – \hspace{.1cm} 1 \right)$$

Praca W nie jest znana. Możemy ją jednak z łatwością obliczyć, ponieważ odpowiada ona polu powierzchni zawartej wewnątrz wykresu w układzie p (V ). Pole to jest równe polu prostokąta o bokach (p₂ – p₁ ) oraz (V₂ – V₁ ), w związku z czym praca W wynosi:

$$W = \left(p_2 \hspace{.15cm} – \hspace{.1cm} p_1 \right) \left(V_2 \hspace{.15cm} – \hspace{.1cm} V_1 \right)$$

Oznacza to, że wyrażenie na ciepło Q_od jest równe:

$$Q_{od} = W \left( \dfrac{1}{\eta} \hspace{.15cm} – \hspace{.1cm} 1 \right) = \left(p_2 \hspace{.15cm} – \hspace{.1cm} p_1 \right) \left(V_2 \hspace{.15cm} – \hspace{.1cm} V_1 \right) \left( \dfrac{1}{\eta} \hspace{.15cm} – \hspace{.1cm} 1 \right)$$

Prawidłowa odpowiedź: wzór pozwalający obliczyć wartość ciepła oddanego przez gaz do chłodnicy wynosi $\hspace{.1cm} Q_{od} = \left(p_2 \hspace{.15cm} – \hspace{.1cm} p_1 \right) \left(V_2 \hspace{.15cm} – \hspace{.1cm} V_1 \right) \left( \dfrac{1}{\eta} \hspace{.15cm} – \hspace{.1cm} 1 \right)$.

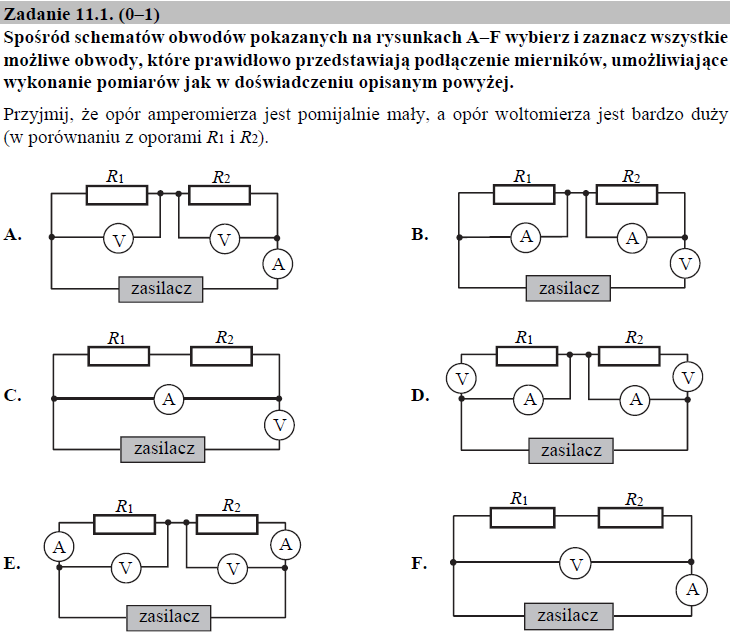
Zadanie to rozwiążemy metodą eliminacji. Zacznijmy od sprawdzenia poprawności podłączenia do obwodu amperomierza oraz woltomierza. Jak wiadomo, amperomierz musi być połączony szeregowo, a woltomierz – równolegle. Warunek ten spełnia tylko obwód z rysunku A, E oraz F. Następnie zastanówmy się nad samym sposobem pomiaru. Z treści zadania wynika, że dla każdego z oporników mierzono napięcie oraz natężenie prądu. Obwód przedstawiony na rysunku 1 nie zawiera żadnych węzłów, powodujących ‘podział’ ładunku elektrycznego, w związku z czym amperomierz mógł być podłączony w dowolnym miejscu tego obwodu. Do każdego z rezystorów (z osobna) musiał być również podłączony woltomierz, aby mierzyć na nim spadek napięcia. Powyższe warunki spełnia więc tylko obwód A oraz E.

Prawidłowa odpowiedź: rysunek A i E.