Arkusz maturalny z fizyki – poziom rozszerzony – rok 2019 („nowa matura”) – zadania nr 5 – 8

Przypadek a)

Ruch planety odbywa się po eliptycznej orbicie. Zwróć uwagę, że punkt A znajduje się w punkcie orbity położonym najbliżej gwiazdy G, z kolei punkt B – w punkcie orbity położonym najdalej od tej gwiazdy. Aby dowiedzieć się jaka zależność występuje pomiędzy wektorem prędkości planety w punkcie A oraz B, skorzystamy z zasady zachowania momentu pędu. Moment pędu planety, podczas jej ruchu po orbicie wokół gwiazdy, przyjmuje stałą, niezmienną wartość, w związku z czym możemy oczekiwać, że moment pędu planety w punkcie A będzie taki sam, jak w punkcie B. Wartość momentu pędu L  możemy obliczyć z poniższego wzoru:

$$L = r \hspace{.05cm} p = r \hspace{.05cm} m \hspace{.05cm} V$$

gdzie r  to odległość planety od gwiazdy, m  – masa planety, a V  to prędkość planety (w zadanej odległości r ).

Zgodnie z powyższym wyrażeniem im większa prędkość V  planety oraz im większa jej odległość r  od gwiazdy, tym większy moment pędu L . Ponieważ odległość punktu A od gwiazdy G jest mniejsza, niż odległość dzieląca punkt B od tejże gwiazdy, dlatego też (aby zasada zachowania momentu pędu była spełniona) prędkość planety w punkcie A musi być większa od jej prędkości w punkcie B: V_1A  > V_1B .

Przypadek b)

W tym przypadku planeta z rysunku 2 oraz 3 porusza się po orbicie kołowej. Aby powiązać prędkość planety z promieniem jej orbity, skorzystamy z drugiej zasady dynamiki Newtona:

$$\vec{F}_{wyp} = m \hspace{.05cm} \vec{a}$$

Siłą wypadkową działającą na planetę jest siła dośrodkowa, której rolę, w tym przypadku, pełni siła wzajemnego przyciągania grawitacyjnego planety oraz gwiazdy. Pod wpływem działania tej siły planeta uzyskuje przyspieszenie dośrodkowe V ²/r , styczne do promienia orbity i zwrócone w kierunku gwiazdy G. Korzystając z w/w informacji możemy zapisać powyższą relację jako:

$$G \hspace{.05cm} \dfrac{m \hspace{.05cm} M}{r^2} = m \hspace{.05cm} \dfrac{V^2}{r}$$

skąd po skróceniu i przekształceniu powyższego wzoru względem prędkości V  planety, dostaniemy:

$$V = \sqrt{\dfrac{G \hspace{.05cm} M}{r}}$$

gdzie M  to masa gwiazdy G, a r  to promień orbity planety.

Widzimy więc, że im większy promień orbity planety, tym mniejsza jest jej prędkość. Zgodnie z rysunkiem 2 oraz 3 promień orbity O₂  jest mniejszy od promienia orbity O₃, a ponieważ punkt A leży na orbicie O₂ , a punkt B – na orbicie O₃ , dlatego też V_2A  > V_3B .

Przypadek c)

Zgodnie z treścią zadania punkt B jest punktem stycznym orbity O₁ i O₃, w związku z czym odległość tego punktu od gwiazdy G jest w obydwu przypadkach taka sama. Może się więc wydawać, że prędkość pierwszej oraz trzeciej planety, w tym punkcie, jest jednakowa. Ale wcale tak nie jest! Pierwsza planeta porusza się po orbicie eliptycznej, dla której to prędkość planety zmienia się wraz ze zmianą położenia planety względem gwiazdy G. Trzecia planeta porusza się po orbicie kołowej – w tym przypadku prędkość planety jest stała tj. nie ulega zmianie wraz ze zmianą położenia planety względem gwiazdy G. Zgodnie ze wzorem przedstawionym w przypadku b) tego zadania, prędkość trzeciej planety w punkcie B wynosi:

$$V_{3B} = \sqrt{\dfrac{G \hspace{.05cm} M}{r}}$$

W przypadku pierwszej planety (poruszającej się po orbicie eliptycznej), wzór opisujący jej prędkość w punkcie B przedstawia się następująco (wzór ten można otrzymać korzystając z zasady zachowania energii mechanicznej oraz z zasady zachowania momentu pędu):

$$V_{1B} = \sqrt{2 \hspace{.03cm} G \hspace{.05cm} M \cdot \dfrac{r_A}{r_B \left( r_A + r_B \right)}}$$

gdzie r_A  to odległość dzieląca gwiazdę G od planety znajdującej się w punkcie A orbity, a r_B  to odległość dzieląca gwiazdę G od planety znajdującej się w punkcie B orbity.

Powyższe wzory są do siebie podobne. Nas interesuje mianownik ułamka w jednym oraz w drugim wzorze. Zauważ, że zgodnie z rysunkami r  < r_B  (r_A  + r_B ), w związku z czym prędkość trzeciej planety w punkcie B jest większa od prędkości pierwszej planety w tymże punkcie: V_1B  < V_3B .

Prawidłowa odpowiedź: V_1A  > V_1B , V_2A  > V_3B , V_1B  < V_3B .

Podpunkt a)

Podpunkt b)

Aby wyznaczyć objętość V_Z  zanurzonej części pojemnika ‘bez obecności’ piasku, wystarczy z wykresu V_Z (m_X ) odczytać wartość V_Z  dla punktu m_X  = 0 g. Zgodnie z wykresem wartość ta wynosi około 150 cm³ (punkt przecięcia pionowej osi wykresu z prostą, dopasowaną do danych eksperymentalnych).

Podpunkt c)

Na wykresie V_Z (m_X ), w podpunkcie a), zaznaczono dwa punkty leżące na brązowej prostej, oznaczone jako A oraz B. Aby wyznaczyć współczynnik kierunkowy tej prostej wystarczy dla obydwu tych punktów odczytać wartość m_X  oraz V_Z  i następnie podstawić je do wzoru $V_Z = A \hspace{.03cm} m_X + B$. Mamy więc:

– dla punktu A:

$$325 \hspace{.05cm} \textrm{cm}^3 = 150 \hspace{.05cm} \textrm{g} \hspace{.05cm} A + B$$

– dla punktu B:

$$475 \hspace{.05cm} \textrm{cm}^3 = 280 \hspace{.05cm} \textrm{g} \hspace{.05cm} A + B$$

W ten sposób otrzymaliśmy układ dwóch równań z dwiema niewiadomymi. Aby obliczyć współczynnik A , mnożymy jedno z tych równań przez (-1) – wówczas współczynnik B  ulegnie skróceniu – i dokonujemy stosownych obliczeń:

$$
\begin{align*}
\begin{cases}
– \hspace{.1cm} 325 \hspace{.05cm} \textrm{cm}^3 = \hspace{.15cm} – \hspace{.1cm} 150 \hspace{.05cm} \textrm{g} \hspace{.05cm} A \hspace{.15cm} – \hspace{.1cm} B \\
475 \hspace{.05cm} \textrm{cm}^3 = 280 \hspace{.05cm} \textrm{g} \hspace{.05cm} A + B
\end{cases}
\hspace{.7cm} \longrightarrow \hspace{.7cm} 150 \hspace{.05cm} \textrm{cm}^3 = 130 \hspace{.05cm} \textrm{g} \hspace{.05cm} A \hspace{.7cm} \longrightarrow \hspace{.7cm} A \approx 1,\hspace{-.05cm}2 \hspace{.05cm} \tfrac{\textrm{cm}^3}{\textrm{g}}
\end{align*}
$$

Prawidłowa odpowiedź: b) objętość zanurzonej części pojemnika (bez piasku) była równa w przybliżeniu 150 cm³, c) A ≈ 1,2 cm³/g.

Podpunkt a)

Pojemnik z piaskiem unosi się na powierzchni cieczy, w związku z czym skierowana w dół siła ciężkości $\vec{F_g}$  musi być równoważona przez skierowaną w górę siłę wyporu $\vec{F}_{wyp}$ :

$$\vec{F_g} = \vec{F}_{wyp} \hspace{1cm} \longrightarrow \hspace{1cm} m \hspace{.05cm} g = m_c \hspace{.05cm} g$$

gdzie m  to masa układu pojemnik-piasek, a m_c  to masa wypartej cieczy.

Masa pojemnika i masa piasku są znane i wynoszą odpowiednio m_p  oraz m_X . Masę wypartej cieczy możemy z kolei powiązać z gęstością ρ  oraz objętością V_Z  cieczy (taka objętość cieczy uległa wyparciu). Zgodnie z treścią zadania objętość V_Z  wynosi V  – V₀ , w związku z czym powyższą zależność możemy zapisać w następującej postaci:

$$\left( m_p + m_X \right) g = \left(V \hspace{.15cm} – \hspace{.1cm} V_0 \right) \rho \hspace{.05cm} g \hspace{1cm} \longrightarrow \hspace{1cm} m_p + m_X = \left(V \hspace{.15cm} – \hspace{.1cm} V_0 \right) \rho$$

Podpunkt b)

Korzystamy ze wzoru wyprowadzonego w podpunkcie a). Naszym celem jest zapisanie go w postaci wyrażenia opisującego zależność objętości V_Z  od masy piasku m_X , które, zgodnie z treścią zadania, wynosi:

$$V_Z = A \hspace{.03cm} m_X + B$$

Gdy wyraz (V  – V₀ ) w równaniu $m_p + m_X = \left(V \hspace{.15cm} – \hspace{.1cm} V_0 \right) \rho$  zastąpimy przez V_Z  i następnie całe to równanie przekształcimy względem objętości V_Z , otrzymamy:

$$V_Z = \dfrac{m_p + m_X}{\rho} = \dfrac{1}{\rho} \hspace{.05cm} m_X + \dfrac{m_p}{\rho}$$

Porównując dwa powyższe równania widzimy, że współczynnik kierunkowy A  jest równy 1/ρ , a wyraz wolny B  = m_p /ρ .

Podpunkt c)

Wiemy, że współczynnik A  wynosi w przybliżeniu 1,2 cm³/g oraz, że A  = 1/ρ , dlatego też:

$$\rho = \dfrac{1}{A} = \dfrac{1}{1,\hspace{-.05cm}2 \hspace{.05cm} \tfrac{\textrm{cm}^3}{\textrm{g}}} \approx 0,\hspace{-.05cm}83 \hspace{.05cm} \tfrac{\textrm{g}}{\textrm{cm}^3}$$

Prawidłowa odpowiedź: a) m_p  + m_X  = (V  – V₀ ) ρ , b) A = 1/ρ , B = m_p /ρ , c) ρ  = 0,83 g/cm³.

Zacznijmy od zapisania wzoru wiążącego ogniskową f  soczewki z jej współczynnikiem załamania światła oraz promieniami jej krzywizny (wzór ten nazywany jest wzorem szlifierzy soczewek):

$$\frac{1}{f} = \left( \dfrac{n}{n_{osr}} \hspace{.1cm} – \hspace{.1cm} 1 \right) \left( \frac{1}{r_1} \hspace{.1cm} – \hspace{.1cm} \frac{1}{r_2} \right)$$

gdzie n  to współczynnik załamania materiału, z jakiego wykonano soczewkę, n_osr  – współczynnik załamania ośrodka, a r₁  i r₂  to promienie krzywizny soczewki.

Aby soczewka mogła skupiać promienie świetlne jej ogniskowa f  musi mieć wartość większą od zera tj. f  > 0. Soczewka dwuwklęsła składa się z dwóch powierzchni załamujących promienie świetlne. Pierwsza z tych powierzchni jest powierzchnią wklęsłą, druga – powierzchnią wypukłą. Oznacza to, że dla soczewki dwuwklęsłej wyrażenie $\left( \dfrac{1}{r_1} \hspace{.15cm} – \hspace{.1cm} \dfrac{1}{r_2} \right)$  jest zawsze ujemne, ponieważ promień r₁  przyjmuje wartość ujemną (promień wklęsłej krzywizny przyjmujemy za ujemny), a promień r₂  – wartość dodatnią (promień wypukłej krzywizny przyjmujemy za dodatni). Spełnienie warunków tego zadania wymaga więc, aby wyrażenie $\left( \dfrac{n}{n_{osr}} \hspace{.1cm} – \hspace{.1cm} 1 \right)$  również było ujemne, ponieważ tylko wtedy ogniskowa soczewki będzie przyjmować wartość dodatnią. Szukamy więc takiego n_osr , dla którego:

$$\dfrac{n}{n_{osr}} \hspace{.1cm} – \hspace{.1cm} 1 < 0 \hspace{1cm} \longrightarrow \hspace{1cm} n < n_{osr}$$

Powyższy wynik oznacza, że szukamy takiego ośrodka, którego współczynnik załamania światła jest większy od współczynnika załamania materiału soczewki, który wynosi 1,6. Warunek ten spełnia tylko ośrodek numer 2 (n_osr  = 1,7) oraz ośrodek numer 3 (n_osr  = 2,2).

Prawidłowa odpowiedź: ośrodek 2 i 3.

Soczewka dwuwklęsła, umieszczona w powietrzu, rozprasza promienie świetlne. Obraz wytwarzany przez soczewkę rozpraszającą jest zawsze obrazem pozornym (tj. powstającym przez przecięcie promienia świetlnego i przedłużenia promienia świetlnego), prostym (nieodwróconym) oraz pomniejszonym. Aby wyznaczyć położenie obrazu przedmiotu P skorzystamy z metody konstrukcyjnej:

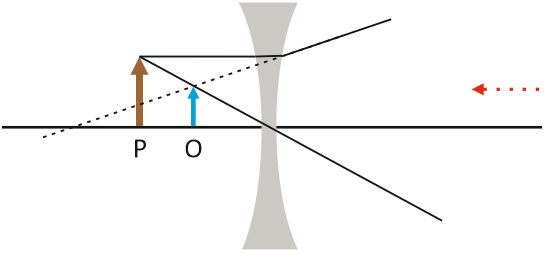
Prawidłowa odpowiedź: rysunek B.

Korzystamy z równania soczewki:

$$\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{f}$$

gdzie f  to ogniskowa soczewki, x  – położenie przedmiotu od środka soczewki, a y  to położenie obrazu przedmiotu od środka soczewki.

Wiemy, że soczewkę tą umieszczoną w powietrzu, w związku z czym obraz przedmiotu będzie znajdował się po tej samej stronie, co przedmiot (obraz pozorny). Oznacza to, że odległość y  przyjmujemy za ujemną, a więc:

$$\dfrac{1}{x} \hspace{.15cm} – \hspace{.1cm} \dfrac{1}{y} = \dfrac{1}{f}$$

Wartość x  oraz y  jest znana, dlatego po przekształceniu powyższego wyrażenia względem ogniskowej soczewki, podstawieniu wartości liczbowych oraz wykonaniu obliczeń, dostaniemy:

$$f = \dfrac{x \cdot y}{x \hspace{.15cm} – \hspace{.1cm} y} = \dfrac{0,\hspace{-.05cm}4 \hspace{.05cm} \textrm{m} \cdot 0,\hspace{-.05cm}25 \hspace{.05cm} \textrm{m}}{0,\hspace{-.05cm}25 \hspace{.05cm} \textrm{m} \hspace{.15cm} – \hspace{.1cm} 0,\hspace{-.05cm}4 \hspace{.05cm} \textrm{m}} \approx \hspace{.15cm} – \hspace{.1cm} 0,\hspace{-.05cm}67 \hspace{.05cm} \textrm{m}$$

Otrzymany wynik jest zgodny z oczekiwaniami, ponieważ zgodnie z konwencją ogniskowa soczewki rozpraszającej przyjmuje wartość ujemną.

Prawidłowa odpowiedź: ogniskowa tej soczewki wynosi w przybliżeniu – 0,67 m.

Przejściu elektronu z poziomu o wyższej energii na poziom o niższej energii towarzyszy emisja fotonu o określonej długości fali. Długość fali tego fotonu zależy od różnicy energii poziomów energetycznych, pomiędzy którymi nastąpił ‘przeskok’ elektronu. Na przykład dla przejścia elektronu z poziomu A o umownej energii E_A  na poziom B o (umownej) energii E_B , mamy:

$$\Delta \hspace{.03cm} E_{AB} = E_A \hspace{.15cm} – \hspace{.1cm} E_B = h \hspace{.05cm} f_{AB} = \dfrac{h \hspace{.05cm} c}{\lambda_{AB}}$$

gdzie h f_AB  to energia fotonu wyemitowanego podczas przejścia elektronu z poziomu A na poziom B, h  – stała Plancka, f_AB  – częstotliwość fotonu, c  – prędkość światła, a λ_AB  to długość fali fotonu.

Powyższy wzór, oczywiście po wprowadzeniu odpowiednich oznaczeń, możemy zastosować dla każdego z przejść elektronów opisanych w treści tego zadania. Energia przejścia elektronu z poziomu A na poziom D (ΔE_AD ) jest równa sumie energii przejść elektronów z poziomów A-B, B-C oraz C-D, w związku z czym możemy zapisać:

$$\Delta \hspace{.03cm} E_{AD} = \Delta \hspace{.03cm} E_{AB} + \Delta \hspace{.03cm} E_{BC} + \Delta \hspace{.03cm} E_{CD}$$

Gdy w miejsce różnicy poziomów energetycznych wstawimy wzory opisujące energię fotonów dla każdego z tych przejść, otrzymamy:

$$\dfrac{h \hspace{.05cm} c}{\lambda_{AD}} = \dfrac{h \hspace{.05cm} c}{\lambda_{AB}} + \dfrac{h \hspace{.05cm} c}{\lambda_{BC}} + \dfrac{h \hspace{.05cm} c}{\lambda_{CD}}$$

i w efekcie:

$$\dfrac{1}{\lambda_{AD}} = \dfrac{1}{\lambda_{AB}} + \dfrac{1}{\lambda_{BC}} + \dfrac{1}{\lambda_{CD}} \hspace{1cm} \longrightarrow \hspace{1cm} \lambda_{AD} = \dfrac{\lambda_{AB} \hspace{.05cm} \lambda_{BC} \hspace{.05cm} \lambda_{CD}}{\lambda_{AB} \hspace{.05cm} \lambda_{BC} + \lambda_{AB} \hspace{.05cm} \lambda_{CD} + \lambda_{BC} \hspace{.05cm} \lambda_{CD}}$$

Prawidłowa odpowiedź: $\hspace{.2cm} \lambda_{AD} = \dfrac{\lambda_{AB} \hspace{.05cm} \lambda_{BC} \hspace{.05cm} \lambda_{CD}}{\lambda_{AB} \hspace{.05cm} \lambda_{BC} + \lambda_{AB} \hspace{.05cm} \lambda_{CD} + \lambda_{BC} \hspace{.05cm} \lambda_{CD}}$ .

Rozwiązania kolejnych zadań z tego arkusza maturalnego znajdziesz na poniższych stronach: