Arkusz maturalny z fizyki – poziom rozszerzony – rok 2015 („nowa matura”) – zadania nr 9 – 12

W zadaniu mamy do czynienia z kondensatorami płaskimi. Pojemność elektryczną tego rodzaju kondensatorów możemy obliczyć stosując poniższy wzór:

$$C = \frac{\varepsilon_0 \hspace{.05cm} \varepsilon_r \hspace{.05cm} S}{d}$$

gdzie:
ε₀  – przenikalność elektryczna próżni,
ε_r  – względna przenikalność elektryczna izolatora dzielącego dwie okładki kondensatora,
S  – powierzchnia okładki kondensatora,
d  – odległość między okładkami kondensatora.

Kondensator A składa się z dwóch płytek przedzielonych czterema kartkami, natomiast kondensator B z dwóch płytek przedzielonych jedną kartką. Powierzchnia S_A  = 0,14 m ⋅ 0,2 m = 0,028 m², powierzchnia S_B  = 0,07 m ⋅ 0,1 m = 0,007 m². Zauważ, że S_A  = 4 S_B . Oznaczmy grubość jednej kartki jako d_k ; wówczas d_k,A  = 4 d_kB . Po wprowadzeniu tych danych do wzoru na pojemność kondensatora dostaniemy szukaną wartość stosunku  $\dfrac{C_A}{C_B}$  równą:

$$\frac{C_A}{C_B} = \frac{\dfrac{\varepsilon_0 \hspace{.05cm} \varepsilon_r \hspace{.05cm} S_A}{d_{k,A}}}{\dfrac{\varepsilon_0 \hspace{.05cm} \varepsilon_r \hspace{.05cm} S_B}{d_{k,B}}} = \frac{S_A \hspace{.05cm} d_{k,B}}{S_B \hspace{.05cm} d_{k,A}} = \frac{4 \hspace{.05cm} S_B \cdot d_{k,B}}{S_B \cdot 4 \hspace{.05cm} d_{k,B}} = 1$$

Prawidłowa odpowiedź:  $\dfrac{C_A}{C_B}$  = 1.

Do jednostek podstawowych układu SI zaliczamy: m, s, kg, A, K, cd, mol (zobacz: Jednostki podstawowe układu SI).

Jednostką współczynnika Seebecka jest  $\rm \frac{V}{K}$.  Korzystając z definicji napięcia:  $U = \frac{W}{q}$, mamy:  $\rm V = \frac{J}{C}$.  Następnie korzystamy z definicji pracy (J), siły (N) oraz przekształconego, względem ładunku q  (C), wzoru na natężenie prądu elektrycznego. Dostaniemy:

$$\rm V = \frac{J}{C} = \frac{N \cdot m}{A \cdot s} = \frac{kg \cdot \tfrac{m}{s^2} \cdot m}{A \cdot s} = \frac{kg \cdot m^2}{A \cdot s^3}$$

Prawidłowa odpowiedź:  $\rm \dfrac{V}{K} = \dfrac{kg \cdot m^2}{A \cdot K \cdot s^3}$.

Podpunkt a)

Wybieramy taką parę materiałów, dla których wyrażenie  $(S_B \hspace{.15cm} – \hspace{.05cm} S_A)$  przyjmuje największą wartość. Spośród podanych materiałów największa różnica  $(S_B \hspace{.15cm} – \hspace{.05cm} S_A)$  występuje dla pary żelazo – nikiel:  $\rm 33,8 \frac{\mu V}{K}$.

Prawidłowa odpowiedź: żelazo – nikiel.

Podpunkt b)

Temperatura wody wrzącej pod normalnym ciśnieniem:  $T_1 = \rm 373,\hspace{-.1cm}15 K$,  temperatura topnienia lodu  $T_2 = \rm 273,\hspace{-.1cm}15 K$,  w związku z czym  $(T_1 \hspace{.15cm} – \hspace{.05cm} T_2) = (373,\hspace{-.1cm}15 \hspace{.05cm} \textrm{K} \hspace{.15cm} – \hspace{.05cm} 273,\hspace{-.1cm}15 \hspace{.05cm} \textrm{K}) = 100 \hspace{.05cm} \textrm{K}$  (w mianowniku jednostki wsp. Seebecka jest Kelwin, dlatego różnicę temperatur musimy wyrazić w Kelwinach). Różnicę  $(S_B \hspace{.15cm} – \hspace{.05cm} S_A)$  znamy, dlatego:

$$U = \left( S_B \hspace{.15cm} – \hspace{.05cm} S_A \right) \left( T_1 \hspace{.15cm} – \hspace{.05cm} T_2 \right) = 33,\hspace{-.1cm}8 \hspace{.05cm} \tfrac{\mu\textrm{V}}{\textrm{K}} \cdot 100 \hspace{.05cm} \textrm{K} = 3,\hspace{-.1cm}38 \hspace{.05cm} \textrm{mV}$$

Prawidłowa odpowiedź: U  = 3,38 mV.

Załóżmy, że termoogniwo spełnia prawo Ohma tj. natężenie prądu I  płynącego przez termoogniwo zmienia się proporcjonalnie do napięcia U.  Załóżmy ponadto, że pojedyncze ogniwo pozwala uzyskać napięcie U  = 5 mV, a opór wewnętrzny termoogniwa wynosi R_w  = 1/100 Ω. Dla tych wartości natężenie prądu płynącego przez termoogniwo jest równe  $I = \frac{U}{R} = 0,5 \hspace{.05cm} \textrm{A}$.

Uzyskanie prądu o natężeniu kilku amperów pod napięciem kilkudziesięciu woltów wymaga połączenia termoogniw w tzw. stosy termoelektryczne (termostosy). Wykonując proste obliczenia sprawdzimy jakie wartości napięcia i prądu możemy uzyskać, gdy połączymy termoogniwa szeregowo oraz równolegle:

Połączenie szeregowe

Bierzemy 5000 termoogniw. Opór wewnętrzny termostosu wynosi:

$$R_{c} = 5000 \cdot R_w = 5000 \cdot \frac{1}{100} = 50 \hspace{.05cm} \Omega$$

Każde ogniwo wytwarza napięcie 5 mV, zatem:

$$U_c = 5000 \cdot 5 \hspace{.05cm} \textrm{mV} = 25 \hspace{.05cm} \textrm{mV}$$

Natężenie prądu jest równe:

$$I_c = \frac{U_c}{R_c} = 0,5 \hspace{.05cm} \textrm{A}$$

Połączenie równoległe

Opór wewnętrzny termostosu wynosi:

$$\frac{1}{R_c} = 5000 \cdot \frac{1}{R_w} \hspace{1cm} \longrightarrow \hspace{1cm} R_c = \frac{R_w}{5000} = 2 \cdot 10^{-6} \hspace{.05cm} \Omega$$

Dla tego rodzaju połączenia napięcie U_c  wynosi:

$$U_c = U = 5 \hspace{.05cm} \textrm{mV}$$

a natężenie prądu jest równe:

$$I_c = \frac{U_c}{R_c} = 5000 \hspace{.05cm} \textrm{A}$$

Stosując połączenie szeregowe termoogniw możemy uzyskać dużą wartość siły elektromotorycznej (napięcia) przy małym natężeniu prądu. Stosując połączenie równoległe termoogniw możemy uzyskać dużą wartość natężenia prądu przy bardzo małym napięciu. Aby czerpać z termostosu prąd o natężeniu kilku amperów pod napięciem kilkudziesięciu woltów należy termoogniwa połączyć w sposób mieszany, czyli szeregowo i równolegle.

Prawidłowa odpowiedź: C – 3.

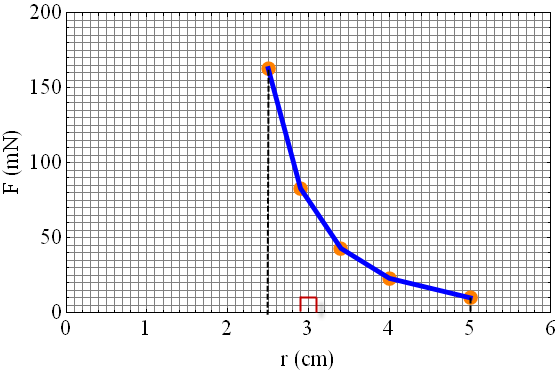
Praca wykonana przeciw sile F  przy zbliżaniu magnesów równa jest polu powierzchni pod krzywą F  (r ). Obszar odpowiadający polu powierzchni, wskazywany przez dwie pionowe, przerywane linie, możemy obliczyć poprzez zliczanie kratek. Jedną taką kratkę, oznaczoną kolorem czerwonym, pokazano na powyższym wykresie. Pole powierzchni czerwonej kratki odpowiada pracy Wk  = 10 mN ⋅ 0,2 cm = 0,02 mJ. Pod krzywą znajduje się ok. 54 takich kratek (bierzemy pod uwagę także ułamki kratek), w związku z czym całkowita praca wynosi około W  = 54 Wk = 1,08 mJ.

Prawidłowa odpowiedź: W  = 1,08 mJ.

Spadek swobodny to rodzaj ruchu odbywający się wyłącznie pod wpływem siły grawitacji. Przyspieszenie z jakim ciało opada na powierzchnię Ziemi równe jest przyspieszeniu ziemskiemu g  = 9,81 m/s². Spadek swobodny można więc traktować jako ruch jednostajnie przyspieszony z przyspieszeniem g. Zmianę wysokości ciała spadającego swobodnie opisuje poniższe równanie:

$$h = h_0 \hspace{.15cm} – \hspace{.05cm} \tfrac{1}{2} \hspace{.05cm} g \hspace{.05cm} t^2$$

gdzie:
h  – wysokość na jakiej znajduje się ciało,
h₀  – wysokość początkowa ciała (wysokość, z której spada ciało),
t  – czas.

Mamy sprawdzić czy spadek magnesu można uznać za spadek swobodny. W tym celu przekształcimy powyższy wzór względem t  i dokonamy obliczeń. Ponieważ h  = 0 m (magnes spadł na ziemię), h₀  = 0,4 m, dlatego:

$$h_0 = \tfrac{1}{2} \hspace{.05cm} g \hspace{.05cm} t^2 \hspace{1cm} \longrightarrow \hspace{1cm} t = \sqrt{\frac{\mathstrut 2 \hspace{.05cm} h}{g}} = \sqrt{\frac{\mathstrut 2 \cdot 0,\hspace{-.1cm}4 \hspace{.05cm} \textrm{m}}{9,\hspace{-.1cm}81 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2}}} = 0,\hspace{-.1cm}29 \hspace{.05cm} \textrm{s}$$

Czas spadania magnesu zmierzony doświadczalnie wyniósł 0,30 ± 0,03 s, w związku z czym spadek magnesu można uznać za swobodny.

Prawidłowa odpowiedź: można.

Jednostajny ruch magnesu na całej długości rurki świadczy o wystąpieniu dodatkowej siły działającej na magnes, zwróconej przeciwnie do siły ciężkości. Tą dodatkową siłą jest siła elektromotoryczna, powstająca na skutek zmian strumienia pola magnetycznego m.in. przy przesuwaniu magnesu względem przewodnika (miedź jest bardzo dobrym przewodnikiem elektrycznym).

Prawidłowa odpowiedź: C – 1.

Obraz przedmiotu uzyskiwany za pomocą soczewki rozpraszającej jest zawsze obrazem pozornym, dlatego bazą do wyznaczenia ogniskowej soczewki rozpraszającej jest wyznaczenie ogniskowej soczewki skupiającej, dającej obraz rzeczywisty przedmiotu (przy założeniu, że x  > f ), oraz ogniskowej układu soczewka rozpraszająca – soczewka skupiająca.

Wyznaczenie ogniskowej soczewki skupiającej

Układ doświadczalny wygląda następująco:

Czynności:

a) Ustawienie świeczki, soczewki skupiającej i ekranu w taki sposób, aby na ekranie powstał ostry obraz świeczki,
f) Pomiar odległości świeczki od soczewki (lub od zestawu soczewek),
g) Pomiar odległości ekranu od soczewki (lub od zestawu soczewek),
h) Zastosowanie wzoru $\frac{1}{f_1} = \frac{1}{x} + \frac{1}{y}$.

Wyznaczenie ogniskowej układu soczewka rozpraszająca – soczewka skupiająca

Układ doświadczalny praktycznie bez zmian – w miejsce soczewki skupiającej wstawiamy układ soczewka rozpraszająca – soczewka skupiająca.

Czynności:

c) Ustawienie świeczki, obu soczewek tuż obok siebie i ekranu w taki sposób, aby na ekranie powstał ostry obraz świeczki,
f) Pomiar odległości świeczki od soczewki (lub od zestawu soczewek),
g) Pomiar odległości ekranu od soczewki (lub od zestawu soczewek),
h) Zastosowanie wzoru  $\tfrac{1}{f} = \frac{1}{x} + \frac{1}{y}$.

Znając ogniskową soczewki skupiającej f₁  i ogniskową układu soczewek f  możemy wyznaczyć ogniskową f₂  soczewki rozpraszającej:

i) Przekształcenie wzoru  $\tfrac{1}{f} = \frac{1}{f_1} + \frac{1}{f_2}$  i obliczenie ogniskowej soczewki rozpraszającej.

Rozwiązania kolejnych zadań z tego arkusza maturalnego znajdziesz na poniższych stronach: