Arkusz maturalny z fizyki – poziom rozszerzony – rok 2015 („nowa matura”) – zadania nr 13 – 16

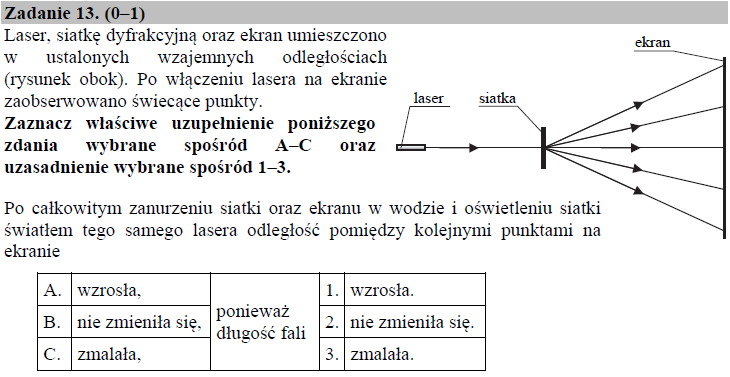
Prędkość rozchodzenia się fal elektromagnetycznych (EM) zależy od ośrodka, w którym fale te się poruszają. Prędkość fal EM w wodzie, ośrodku dużo gęstszym od powietrza, będzie mniejsza, niż w powietrzu.

Zgodnie ze wzorem  $V = \lambda \hspace{.05cm} f$,  prędkość fal EM jest wprost proporcjonalna do długości fali i częstotliwości jej drgań. Podczas przejścia fal EM przez dwa różne ośrodki, zmianie (oprócz prędkości) ulega tylko długość fali (częstotliwość drgań jest stała). W związku z tym faktem, długość fali światła laserowego przechodzącego przez warstwę wody musi ulec zmniejszeniu. Mniejsza długość fali to mniejszy kąt ugięcia światła na szczelinie (równanie siatki dyfrakcyjnej:  $d \hspace{.05cm} {\rm sin} \hspace{.03cm} \theta = n \hspace{.05cm} \lambda$) i w konsekwencji mniejsza odległość pomiędzy kolejnymi punktami na ekranie.

Prawidłowa odpowiedź: C – 3.

Jeden gram polonu  $^{210}\textrm{Po}$  wydziela ciepło o mocy około 140 W. Czas połowicznego zaniku tego izotopu wynosi 139 dni, co oznacza, że po upływie dwóch lat, czyli 730 lub 731 dni (przy założeniu roku przestępnego), z jednego grama  $^{210}\textrm{Po}$  pozostanie około 0,03125 g polonu (założyliśmy, że ilość jąder tego izotopu będzie pięciokrotnie maleć o połowę, bo 5 ⋅ 139 dni = 695 dni). Próbka zawierająca 0,03125 g polonu wydzieli ciepło o mocy około 4,375 W, co stanowi mniej niż 1/30 mocy początkowej.

Prawidłowa odpowiedź: D.

Stwierdzenie to wynika z drugiej zasady termodynamiki zgodnie, z którą nie jest możliwe zbudowanie perpetuum mobile drugiego rodzaju, czyli urządzenia, które pobierając ciepło z otoczenia zamieniałoby je całkowicie na pracę mechaniczną (w tym przypadku: energię elektryczną).

Polski fizyk Marian Smoluchowski (1872 – 1917) sformułował drugą zasadę termodynamiki następująco:

Korzystamy z zasady zachowania energii dla zjawiska fotoelektrycznego zewnętrznego:

$$E_f = W + E_k$$

gdzie:
E_f  – energia fotonu padającego na katodę fotokomórki,
W  – praca wyjścia elektronu z materiału katody,
E_k  – energia kinetyczna elektronu wybitego z powierzchni katody.

Zjawisko fotoelektryczne zewnętrzne występuje tylko wtedy, gdy energia fotonu E_f  padającego np. na katodę fotokomórki jest równa co najmniej pracy wyjścia materiału katody. Gdy E_f  > W, elektron wybity z powierzchni katody uzyskuje dodatkowo energię kinetyczną E_k .

Aby dowiedzieć się, z którego z metali, oświetlanego światłem o długości fali  λ = 370 nm, możemy wykonać katodę, obliczymy energię fotonów odpowiadającą  λ = 370 nm i następnie porównamy ją z pracą wyjścia dla każdego metalu. Dla E_f  ≥ W  otrzymamy rozwiązanie tego zadania.

Energię fotonu obliczymy z poniższego wzoru:

$$E_f = h \hspace{.05cm} \nu = h \hspace{.05cm} \frac{c}{\lambda}$$

gdzie:
h  – stała Plancka równa 6,626 ⋅ 10^-34 J ⋅ s,
c  – prędkość światła w próżni równa 3 ⋅ 10⁸ m/s,
λ  – długość fali fotonu równa 370 nm.

Po wykonaniu obliczeń, mamy:

$$E_f = \frac{6,\hspace{-.1cm}626 \cdot 10^{-34} \hspace{.05cm} \textrm{J} \cdot \textrm{s} \cdot 3 \cdot 10^8 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}}}{370 \cdot 10^{-9} \hspace{.05cm} \textrm{m}} = 5,\hspace{-.1cm}4 \cdot 10^{-19} \hspace{.05cm} \textrm{J} = 3,\hspace{-.1cm}4 \hspace{.05cm} \textrm{eV}$$

Z podanej listy metali tylko cez i lit mają pracę wyjścia mniejszą od energii fotonu, dlatego to właśnie z tych dwóch materiałów będzie można wykonać katodę fotokomórki.

Prawidłowa odpowiedź: cez, lit.

Przyłożenie napięcia do elektrod fotokatody skutkuje przepływem elektronów od katody, z powierzchni której zostały wybite, do anody fotokomórki. Im większa liczba wybitych elektronów, tym większe natężenie prądu. Zależność I  (U ) przedstawiona na powyższym wykresie odpowiada sytuacji, w której wszystkie elektrony wybite z katody dotarły do anody fotokomórki (osiągnięto tzw. stan nasycenia), w związku z czym dalszy wzrost napięcia nie może spowodować wzrostu natężenia prądu elektrycznego.

Podpunkt a)

Korzystamy z definicji mocy:

$$P = \frac{W}{t} = \frac{E_{cf}}{t}$$

gdzie:
P  – moc promieniowania lasera,
E_cf  – całkowita energia strumienia fotonów padających na powierzchnię katody,
t  – czas.

Energia całkowita E_cf  strumienia fotonów wynosi:

$$E_{cf} = n_f \cdot E_f = n_f \cdot \frac{h \hspace{.05cm} c}{\lambda}$$

gdzie:
n_f  – liczba fotonów padających na katodę,
E_f  – energia pojedynczego fotonu.

Po podstawieniu powyższej zależności do wzoru na moc promieniowania, otrzymamy:

$$P = \frac{n_f \cdot \frac{h \hspace{.05cm} c}{\lambda}}{t} \hspace{1cm} \longrightarrow \hspace{1cm} n_f = \frac{P \hspace{.05cm} t \hspace{.05cm} \lambda}{h \hspace{.05cm} c}$$

i w konsekwencji:

$$n_f = \frac{6 \cdot 10^{-6} \hspace{.05cm} \textrm{W} \cdot 1 \hspace{.05cm} \textrm{s} \cdot 370 \cdot 10^{-9} \hspace{.05cm} \textrm{m}}{6,\hspace{-.1cm}626 \cdot 10^{-34} \hspace{.05cm} \textrm{J} \cdot \textrm{s} \cdot 3 \cdot 10^8 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}}} = 1,\hspace{-.1cm}1 \cdot 10^{13}$$

Prawidłowa odpowiedź: Liczba fotonów n_f  = 1,1 ⋅ 10¹³.

Podpunkt b)

Korzystamy z definicji natężenia prądu elektrycznego:

$$I = \frac{q}{t}$$

gdzie:
I  – natężenie prądu elektrycznego,
q  – ładunek elektryczny,
t  – czas.

Po przekształceniu powyższego wzoru względem ładunku q, podstawieniu wartości liczbowych i wykonaniu obliczeń, dostaniemy:

$$q = I \cdot t = 5 \cdot 10^{-7} \hspace{.05cm} \textrm{A} \cdot 1 \hspace{.05cm} \textrm{s} = 5 \cdot 10^{-7} \hspace{.05cm} \textrm{C}$$

Ładunek elektryczny pojedynczego elektronu wynosi  $1 \hspace{.05cm} e = 1,\hspace{-.1cm}6021 \cdot 10^{-19} \hspace{.05cm} \textrm{C}$. Aby obliczyć liczbę elektronów przepływających w ciągu 1 s w obwodzie, wystarczy podzielić całkowity ładunek q  przez ładunek pojedynczego elektronu e :

$$n_e = \frac{q}{e} = \frac{5 \cdot 10^{-7} \hspace{.05cm} \textrm{C}}{1,\hspace{-.1cm}6021 \cdot 10^{-19} \hspace{.05cm} \textrm{C}} = 3,\hspace{-.1cm}1 \cdot 10^{12}$$

Prawidłowa odpowiedź: Liczba elektronów n_e  = 3,1 ⋅ 10¹².

Podpunkt c)

Znamy liczbę fotonów padających na katodę. Wiemy ile elektronów zostało wybitych z powierzchni katody. Liczba fotonów, która spowodowała wybicie elektronów z katody wynosi:

$$x = \frac{n_e}{n_f} \cdot 100\% = \frac{3,\hspace{-.1cm}1 \cdot 10^{12}}{1,\hspace{-.1cm}1 \cdot 10^{13}} \cdot 100\% = 28,\hspace{-.1cm}2\%$$

Powyższa wartość to nic innego jak wydajność zjawiska fotoelektrycznego zewnętrznego.

Prawidłowa odpowiedź: 28,2% fotonów spowodowało wybicie elektronów z katody.

Głównym źródłem energii Słońca jest proces syntezy termojądrowej zachodzący w jego wnętrzu, polegający na łączeniu się jąder lekkich w jądra ciężkie.

Układ Słoneczny nie znajduje się, jak początkowo sądzono, w centrum Drogi Mlecznej, lecz jest od niego oddalony o ok. 30 tys. lat świetlnych.

Wszechświat, którego częścią jest nasz Układ Słoneczny, stale się rozszerza, czego dowodem jest m.in. zjawisko przesunięcia ku czerwieni widma promieniowania elektromagnetycznego pochodzącego z odległych gwiazd, czy galaktyk.

Rozwiązania kolejnych zadań z tego arkusza maturalnego znajdziesz na poniższych stronach: