Arkusz maturalny z fizyki – poziom rozszerzony – rok 2015 („nowa matura”) – zadania nr 1 – 4

Aby obręcz po upadku mogła wrócić do gimnastyczki, kierunek obrotu obręczy musi być zgodny z kierunkiem ruchu wskazówek zegara .

Przy braku oporu powietrza wartość prędkości ruchu obrotowego obręczy nie będzie ulegać zmianie, w związku z czym prędkość obręczy będzie taka sama od momentu wyrzucenia aż do upadku.

Prawidłowa odpowiedź: D.

Zgodnie z zasadą zachowania momentu pędu moment pędu ciała pozostaje stały, gdy nie działa na nie żaden moment siły zewnętrznej. Brak obecności momentów sił zewnętrznych działających na obręcz powoduje, że kierunek wektora momentu pędu obręczy jest zachowany, w związku z czym obręcz po upadku w punkcie C może toczyć się w kierunku gimnastyczki.

Prawidłowa odpowiedź: zasada zachowania momentu pędu.

Powrót obręczy z położenia C do gimnastyczki jest skutkiem działania siły tarcia kinetycznego, zwróconej przeciwnie do kierunku ruchu obręczy.

Prawidłowa odpowiedź: B.

Gdy wózek znajduje się w spoczynku oraz, gdy porusza się ruchem jednostajnym prostoliniowym poziom cieczy w naczyniu jest nachylony pod pewnym kątem do powierzchni równi:

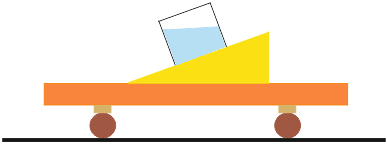
układ wagon - równia pochyła i naczynie wypełnione wodą - rysunek schematyczny - nowa matura 2015 - zadanie nr 2

Aby powierzchnia wody w naczyniu stała się równoległa do powierzchni równi, dodatkowa siła działająca na wózek musi być zwrócona w lewo (przyłożenie siły w prawą stronę jeszcze bardziej zwiększyłoby kąt nachylenia poziomu wody). Dla tak zdefiniowanego układu kierunek wózka nie wpłynie na położenie poziomu wody w naczyniu, dlatego ruch wózka może odbywać się w lewo lub w prawo.

Prawidłowa odpowiedź: B – 3.

Zdanie 1

Siła naciągu liny w każdym jej punkcie ma taką samą wartość, w związku z czym zdanie 1 jest fałszywe.

Zdanie 2

W początkowej fazie ruchu kąt β przyjmuje maksymalną wartość. Wraz z oddalaniem się traktora od podpory, kąt β stopniowo maleje, dlatego zdanie 2 jest prawdziwe.

Zdanie 3

Jeden koniec liny przymocowany jest do traktora, drugi koniec do górnego końca słupa, odległego o l (l – wysokość słupa) od jego podstawy. Im większa wysokość, tym większa siła potrzebna do postawienia słupa, a więc tym większa siła naciągu liny.

Prawidłowa odpowiedź: 1 – F, 2 – P, 3 – P.

Słup traktujemy jak bryłę sztywną. Wiemy, że środek masy słupa znajduje się w połowie jego długości l, w związku z czym siła ciężkości $\vec{F_g}$ działająca na słup jest przyłożona do niego właśnie w tym punkcie. Siłą działającą w tym samym kierunku, lecz przeciwnie zwróconą do siły ciężkości jest składowa $\vec{N_y}$ siły naciągu liny $\vec{N}$ równa $\vec{N_y} = \vec{N} \hspace{.05cm} \textrm{sin} \hspace{.03cm} \alpha$ :

podnoszenie słupa - rysunek schematyczny - nowa matura 2015 - zadanie nr 3_2

Aby obliczyć wartość siły naciągu liny skorzystamy z równowagi momentów sił: ciężkości oraz naciągu liny. Obydwa momenty sił zapiszemy względem osi przechodzącej przez obrotową podstawę walca, oznaczoną na powyższym rysunku linią przerywaną. Ramieniem siły ciężkości $\vec{F_g}$ jest odległość od środka masy do podstawy walca równa $\frac{l}{2}$, a ramieniem składowej siły naciągu $\vec{N_y}$ jest odległość od końca słupa do podstawy walca równa $l$. Z równowagi momentów sił mamy:

$$M_g = M_n \hspace{1cm} \longrightarrow \hspace{1cm} m \hspace{.05cm} g \hspace{.05cm} \tfrac{l}{2} = N \hspace{.05cm} \textrm{sin} \hspace{.03cm} \alpha \hspace{.05cm} l$$

Po przekształceniu i podstawieniu wartości liczbowych, dostaniemy:

$$N = \frac{m \hspace{.05cm} g}{2 \hspace{.05cm} \textrm{sin} \hspace{.03cm} \alpha} = \frac{2000 \hspace{.05cm} \textrm{kg} \cdot 9,\hspace{-.1cm}81 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2}}{2 \cdot \textrm{sin} \hspace{.03cm} 15^{\textrm{o}}} \cong 37,\hspace{-.1cm}9 \hspace{.05cm} \textrm{kN}$$

Prawidłowa odpowiedź: N = 37,9 kN.

W tym zadaniu korzystamy z zasady zachowania energii mechanicznej. W chwili zerwania liny całkowita energia mechaniczna słupa równa jest energii potencjalnej grawitacji słupa $E_p = m \hspace{.05cm} g \hspace{.05cm} \frac{l}{2}$ – środek masy słupa znajduje się w połowie jego długości, w związku z czym całkowita masa słupa skupiona jest właśnie w tym punkcie. W chwili upadku całkowita energia mechaniczna słupa równa jest energii kinetycznej ruchu obrotowego słupa $E_k = \frac{1}{2} \hspace{.05cm} I \hspace{.05cm} \omega^2$, gdzie I to moment bezwładności słupa równy $I = \frac{1}{3} \hspace{.05cm} m \hspace{.05cm} l^2$, ω – prędkość kątowa słupa równa $\omega = \frac{V}{l}$. Po przyrównaniu tych dwóch rodzajów energii otrzymamy:

$$m \hspace{.05cm} g \hspace{.05cm} \tfrac{l}{2} = \tfrac{1}{2} \hspace{.05cm} I \hspace{.05cm} \omega^2 = \tfrac{1}{2} \cdot \tfrac{1}{3} \cdot m \hspace{.05cm} l^2 \cdot \frac{V^2}{l^2} = \tfrac{1}{6} \hspace{.05cm} m \hspace{.05cm} V^2$$

i w konsekwencji:

$$V = \sqrt{\mathstrut 3 \hspace{.05cm} g \hspace{.05cm} l} = \sqrt{\mathstrut 3 \cdot 9,\hspace{-.1cm}81 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2} \cdot 12 \hspace{.05cm} \textrm{m}} = 18,\hspace{-.1cm}8 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}}$$

Prawidłowa odpowiedź: V = 18,8 m/s.

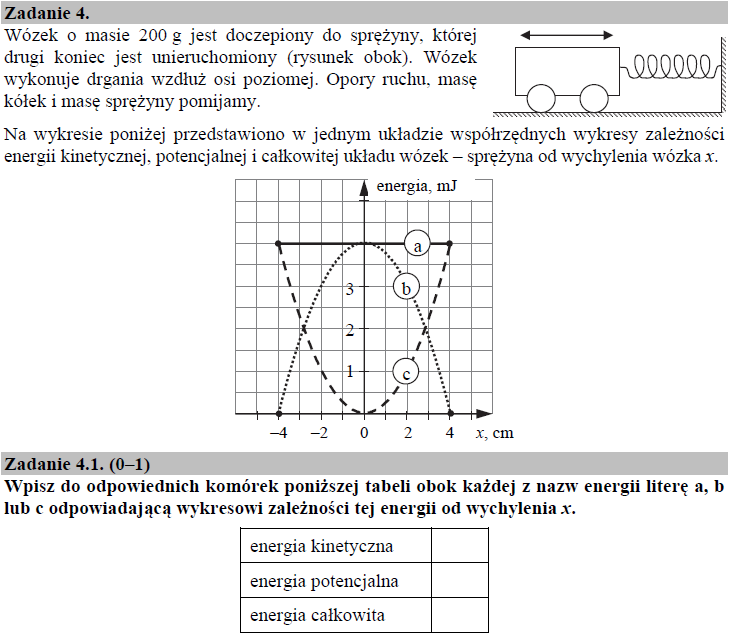
Wartość energii potencjalnej E_p układu wózek – sprężyna zależy wprost proporcjonalnie od wychylenia układu z położenia równowagi. Dla położenia x = 0 m E_p = 0 J, a dla x = x_max E_p = E_p,max. Zależność E_p (x ) poprawnie opisuje więc krzywa C.

Zupełnie odwrotna sytuacja, do opisanej powyżej, występuje w przypadku energii kinetycznej E_k układu wózek – sprężyna. Dla położenia x = 0 m E_k = E_k,max, a dla x = x_max E_k = 0 J. Zależność E_k (x ) poprawnie opisuje więc krzywa B.

Energia całkowita układu drgającego zawsze pozostaje stała w czasie (przy założeniu braku oporów ruchu), dlatego zależność E_c (x ) przedstawia krzywa A.

Więcej informacji znajdziesz w artykule Energia w ruchu harmonicznym.

Prawidłowa odpowiedź: energia kinetyczna – B, energia potencjalna – C, energia całkowita – A.