Arkusz maturalny z fizyki – poziom podstawowy – rok 2016 („stara matura”) – zadania nr 11 – 15

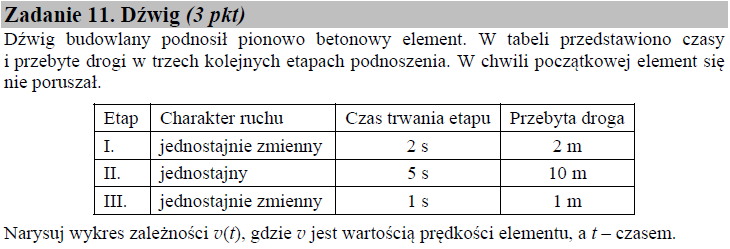
Etap 1

Betonowy element poruszał się ruchem jednostajnie zmiennym (zakładamy, że przyspieszenie było stałe w czasie). W chwili początkowej jego prędkość była równa V₀₁ = 0 m/s. W chwili końcowej tj. po przebyciu drogi s₁ = 2 m jego prędkość była równa V_k1. Korzystając ze wzoru na prędkość i drogę w ruchu jednostajnie przyspieszonym, dostaniemy:

$$V_{k1} = V_{01} + a_1 \hspace{.05cm} t_1 = a_1 \hspace{.05cm} t_1 \hspace{1cm} , \hspace{1cm} s_1 = V_{01} \hspace{.05cm} t_1 + \frac{a_1 \hspace{.05cm} t_1^2}{2} = \frac{a_1 \hspace{.05cm} t_1^2}{2}$$

Po przekształceniu wzoru na drogę s₁  względem przyspieszenia a₁, otrzymamy:

$$a_1 = \frac{2 \hspace{.05cm} s_1}{t_1^2} = \frac{2 \cdot 2 \hspace{.05cm} \textrm{m}}{\left( 2 \hspace{.05cm} \textrm{s} \right)^2} = 1 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2}$$

i w konsekwencji:

$$V_{k1} = a_1 \hspace{.05cm} t_1 = 1 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2} \cdot 2 \hspace{.05cm} \textrm{s} = 2 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}}$$

Etap 2

Betonowy element poruszał się ruchem jednostajnym prostoliniowym. Podczas trwania tego ruchu prędkość ciała pozostaje stała. Ponieważ prędkość końcowa V_k1  jest zarazem prędkością początkową V₀₂, dlatego V₂  = V₀₂  = 2 m/s:

$$V_2 = V_{02} = \frac{s_2}{t_2} = \frac{10 \hspace{.05cm} \textrm{m}}{5 \hspace{.05cm} \textrm{s}} = 2 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}}$$

Etap 3

Sytuacja podobna do opisu Etapu 1. Różnica polega na tym, że betonowy element po przebyciu drogi s₃, z prędkością początkową V₀₃  = 2 m/s, uległ zatrzymaniu. W związku z tym faktem prędkość końcowa V_k3  = 0 m/s.

Mamy wszystkie dane niezbędne do sporządzeniu wykresu V (t ), zatem:

Obliczmy na początek stałą sprężystości k  sprężyny. Wiemy, że pod wpływem siły zewnętrznej  $\vec{F_{z}}$  o wartości 1 N sprężyna rozciąga się o x  = 1 cm = 0,01 m. Skutkiem rozciągnięcia sprężyny jest powstanie przeciwnie skierowanej siły sprężystości  $\vec{F}$, w związku z czym  $\vec{F_z} = \hspace{.1cm} – \vec{F}$. Ponieważ siła sprężystości $F = \hspace{.1cm} – k x$,  dostaniemy:

$$F_z = \hspace{.15cm} – \hspace{.05cm} \left( \hspace{.15cm} – \hspace{.05cm} k \hspace{.05cm} x \right) = k \hspace{.05cm} x \hspace{1cm} \longrightarrow \hspace{1cm} k = \frac{F_z}{x} = \frac{1 \hspace{.05cm} \textrm{N}}{0,\hspace{-.1cm}01 \hspace{.05cm} \textrm{m}} = 100 \hspace{.05cm} \tfrac{\textrm{N}}{\textrm{m}}$$

Po przyczepieniu sprężyny do klocka o masie m  = 1 kg i ponownemu przyłożeniu siły zewnętrznej, na układ klocek – sprężyna, w kierunku poziomym, zaczną oddziaływać dwie siły: siła sprężystości  $\vec{F}$  oraz siła tarcia statycznego  $\vec{F_{TS}}$. Siły te zwrócone są w tym samym kierunku, ponieważ obydwie przeciwstawiają się zarówno zwiększeniu wydłużenia sprężyny, jak i ruchowi klocka. Z drugiej zasady dynamiki Newtona mamy:

$$\vec{F}_{TS} + \vec{F} = m \hspace{.05cm} \vec{a} = 0 \hspace{1cm} \longrightarrow \hspace{1cm} \vec{F}_{TS} = \hspace{.15cm} – \hspace{.05cm} \vec{F}$$

Zauważ, że siły te są równe co do wartości. Sprężyna rozciągnęła się o x₁ = 5 cm = 0,05 m, zatem:

$$F_{TS} = \hspace{.15cm} – \hspace{.05cm} \left( \hspace{.15cm} – \hspace{.05cm} k \hspace{.05cm} x_1 \right) = k \hspace{.05cm} x_1 = 100 \hspace{.05cm} \tfrac{\textrm{N}}{\textrm{m}} \cdot 0,\hspace{-.1cm}05 \hspace{.05cm} \textrm{m} = 5 \hspace{.05cm} \textrm{N}$$

Prawidłowa odpowiedź: F_TS  = F  = 5 N.

Korzystamy ze wzoru  $F_{TS} = k x$.  Siła tarcia statycznego  $F_{TS} = f_s \hspace{.05cm} m \hspace{.05cm} g$,  gdzie f_s  to współczynnik tarcia statycznego, m  – masa klocka, g  – przyspieszenie ziemskie, dlatego:

$$x_2 = \frac{f_s \hspace{.05cm} m \hspace{.05cm} g}{k} = \frac{0,\hspace{-.1cm}65 \cdot 1 \hspace{.05cm} \textrm{kg} \cdot 9,\hspace{-.1cm}81 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2}}{100 \hspace{.05cm} \tfrac{\textrm{N}}{\textrm{m}}} = 6,\hspace{-.1cm}4 \hspace{.05cm} \textrm{cm}$$

Prawidłowa odpowiedź: maksymalne wydłużenie sprężyny wynosi x₂  = 6,4 cm.

Układ klocek – sprężyna porusza się. Siłami działającymi na ten układ są: siła zewnętrzna  $\vec{F_{z1}}$  oraz siła tarcia kinetycznego  $\vec{F_{TK}}$, występująca pomiędzy klockiem a podłożem. Prędkość układu pozostaje stała, zatem siły $\vec{F_{z1}}$  i  $\vec{F_{TK}}$ muszą się równoważyć:

$$F_{z1} = F_{TK} = f_k \hspace{.05cm} m \hspace{.05cm} g \hspace{1cm} \longrightarrow \hspace{1cm} f_k = \frac{F_{z1}}{m \hspace{.05cm} g}$$

Po podstawieniu wartości liczbowych, dostaniemy:

$$f_k = \frac{5 \hspace{.05cm} \textrm{N}}{1 \hspace{.05cm} \textrm{N} \cdot 9,\hspace{-.1cm}81 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2}} = 0,\hspace{-.1cm}51$$

Prawidłowa odpowiedź: współczynnik tarcia kinetycznego wynosi f_k  = 0,51.

Siłami działającymi na układ sprężyna – ciężarek są siła ciężkości  $\vec{F}_g$  związana z ciężarkiem o masie m  oraz siła sprężystości  $\vec{F}$  związana ze sprężyną o stałej sprężystości k, zwrócona przeciwnie do siły ciężkości. Z warunku równowagi tych dwóch sił (bo układ sprężyna – ciężarek nie zmienia swojego położenia), dostaniemy:

$$m \hspace{.05cm} g = \hspace{.15cm} – \hspace{.05cm} k \hspace{.05cm} \Delta \hspace{.03cm} x$$

gdzie:
g  – przyspieszenie ziemskie,
Δx  – długość rozciągnięcia sprężyny po zawieszeniu na niej ciężarka – wydłużenie sprężyny możemy bardzo łatwo zmierzyć (podczas pomiaru układ sprężyna – ciężarek pozostaje nieruchomy, dzięki czemu błąd pomiaru jest dużo mniejszy).

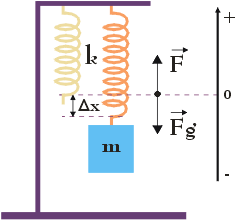
Zgodnie z powyższym rysunkiem Δx  przyjmuje ujemną wartość, w związku z czym wyrażenie – k Δx  będzie dodatnie.

Po przekształceniu powyższego równania względem g, otrzymamy:

$$g = \hspace{.15cm} – \hspace{.05cm} \frac{k}{m} \hspace{.05cm} \Delta \hspace{.03cm} x$$

Wielkości k  oraz m  powiążemy z częstością kołową ω  drgań tego układu (zobacz: Siła w ruchu harmonicznym):

$$\omega = \sqrt{\frac{\mathstrut k}{m}} \hspace{2cm} \longrightarrow \hspace{2cm} \omega^2 = \frac{k}{m}$$

z kolei częstość kołową ω  z okresem drgań T :

$$\omega^2 = \left( \frac{2 \hspace{.05cm} \pi}{T} \right)^2 = \frac{k}{m}$$

Po podstawieniu powyższego równania do wzoru na przyspieszenie ziemskie dostaniemy (Δx  jest ujemne, dlatego przyspieszenie ziemskie będzie mieć dodatnią wartość):

$$g = \hspace{.15cm} – \hspace{.05cm} \left( \frac{2 \hspace{.05cm} \pi}{T} \right)^2 \Delta \hspace{.03cm} x$$

Prawidłowa odpowiedź: należy wybrać pomiar b).

Wynik eksperymentu (wartość przyspieszenia) jest uzależniony od dokładności pomiaru wielkości mierzonych, czyli czasu i długości. Zmniejszenie niepewności pomiaru, i tym samym uzyskanie dokładniejszej wartości przyspieszenia ziemskiego, można uzyskać stosując metodę stosowaną np. na zajęciach laboratoryjnych z fizyki: dziesięciokrotny pomiar okresu drgań oraz wydłużenia sprężyny i obliczenie wartości średniej dla tych dwóch wielkości fizycznych.

Zacznijmy od ustalenia znaku ładunku q_B  zgromadzonego na kulce B. Siłami działającymi na kulkę B są siła ciężkości  $\vec{F}_g$  oraz siła oddziaływania elektrostatycznego  $\vec{F}_{BA}$  (siła z jaką kulka A działa na kulkę B). Wiemy, że siły  $\vec{F}_g$  i  $\vec{F}_{BA}$  równoważą się. Siła ciężkości jest zawsze zwrócona w dół, zatem siła oddziaływania elektrostatycznego musi być zwrócona w górę (w kierunku przeciwnym do zwrotu siły ciężkości):

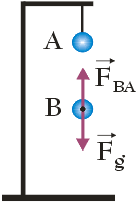
Zgodnie z tym faktem, na kulce B musi być zgromadzony ładunek ujemny, bo tylko wtedy siła  $\vec{F}_{BA}$  zwrócona jest ku górze.

Obliczmy teraz wartość ładunku q_B. Z warunku równowagi sił dostaniemy:

$$\hspace{.15cm} – \hspace{.05cm} k \hspace{.05cm} \frac{q_A \hspace{.05cm} q_B}{r^2} = m_B \hspace{.05cm} g$$

skąd po przekształceniu względem q_B , otrzymamy:

$$q_B = \hspace{.15cm} – \hspace{.05cm} \frac{m_B \hspace{.05cm} g \hspace{.1cm} r^2}{k \hspace{.05cm} q_A}$$

Po podstawieniu wartości liczbowych uzyskamy:

$$q_B = \hspace{.15cm} – \hspace{.05cm} \frac{2 \cdot 10^{-4} \hspace{.05cm} \textrm{kg} \cdot 9,\hspace{-.1cm}81 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2} \cdot 9 \cdot 10^{-4} \hspace{.05cm} \textrm{m}^2}{9 \cdot 10^9 \hspace{.05cm} \tfrac{\textrm{N} \hspace{.05cm} \cdot \hspace{.05cm} \textrm{m}^2}{\textrm{C}^2} \cdot 15 \cdot 10^{-9} \hspace{.05cm} \textrm{C}} = \hspace{.15cm} – \hspace{.05cm} 13,\hspace{-.1cm}1 \hspace{.05cm} \textrm{nC}$$

Prawidłowa odpowiedź: na kulce B zgromadził się ładunek ujemny o wartości – 13,1 nC.

W zadaniu tym mamy do czynienia ze zjawiskiem indukcji elektrostatycznej. Przysunięcie dodatnio naładowanej kulki A do metalowej kuli C (przewodnika) spowoduje przemieszczenie ładunków – elektronów – w kuli. Skutkiem tego zjawiska będzie wystąpienie tzw. ładunku indukowanego na powierzchni kuli, przy czym część powierzchni kuli bliższa kulce A będzie naładowana ujemnie, a przeciwległa jej część – dodatnio (kula jako całość pozostanie obojętna elektrycznie). W konsekwencji dodatnio naładowana kulka A odchyli się w stronę ujemnie naładowanej powierzchni metalowej kuli.

Prawidłowa odpowiedź: 1 – I.

Odległość między kulkami wzrosła, dlatego wartość siły oddziaływania elektrostatycznego zmalała. Wartość siły ciężkości nie uległa zmianie, w związku z czym $\vec{F}_g > \vec{F}_{BA}$. Konsekwencją tej sytuacji będzie zmiana położenia kulki B względem kulki A – kulka B zacznie spadać.

Prawidłowa odpowiedź: 3 – III.

Odległość obrazu od zwierciadła przyjmuje wartość dodatnią, zatem obraz znajduje się po tej samej stronie zwierciadła co przedmiot. Oznacza to, że otrzymany obraz jest obrazem rzeczywistym. Wszystkie obrazy rzeczywiste uzyskane przy pomocy zwierciadła wklęsłego są obrazami odwróconymi. Zwróć uwagę, że odległość przedmiotu od zwierciadła jest równa odległości obrazu od zwierciadła, w związku z czym powiększenie obrazu p  jest równe jedności i dlatego uzyskany obraz jest tej samej wielkości co przedmiot.

Prawidłowa odpowiedź: obraz rzeczywisty, odwrócony, tej samej wielkości co przedmiot.

Z pomiaru nr 1 mamy: odległość przedmiotu od zwierciadła x  = 15 cm, odległość obrazu od zwierciadła y  = 30 cm. Związek pomiędzy x, y  i f  opisuje równanie zwierciadła:

$$\frac{1}{x} + \frac{1}{y} = \frac{1}{f}$$

Po podstawieniu wartości liczbowych, dostaniemy:

$$\frac{1}{15 \hspace{.05cm} \textrm{cm}} + \frac{1}{30 \hspace{.05cm} \textrm{cm}} = \frac{2}{30 \hspace{.05cm} \textrm{cm}} + \frac{1}{30 \hspace{.05cm} \textrm{cm}} = \frac{3}{30 \hspace{.05cm} \textrm{cm}} = \frac{1}{10 \hspace{.05cm} \textrm{cm}} = \frac{1}{f}$$

i w efekcie:

$$f = 10 \hspace{.05cm} \textrm{cm}$$

Prawidłowa odpowiedź: ogniskowa zwierciadła jest równa 10 cm.

Wielkością szukaną jest odległość obrazu od zwierciadła y. Korzystając z równania zwierciadła, otrzymamy:

$$\frac{1}{y} = \frac{1}{f} \hspace{.15cm} – \hspace{.05cm} \frac{1}{x} = \frac{1}{10 \hspace{.05cm} \textrm{cm}} \hspace{.15cm} – \hspace{.05cm} \frac{1}{30 \hspace{.05cm} \textrm{cm}} = \frac{3}{30 \hspace{.05cm} \textrm{cm}} \hspace{.15cm} – \hspace{.05cm} \frac{1}{30 \hspace{.05cm} \textrm{cm}} = \frac{2}{30 \hspace{.05cm} \textrm{cm}} = \frac{1}{15 \hspace{.05cm} \textrm{cm}}$$

i w konsekwencji:

$$y = 15 \hspace{.05cm} \textrm{cm}$$

Prawidłowa odpowiedź: odległość obrazu od zwierciadła wynosi 15 cm.

Rozwiązania kolejnych zadań z tego arkusza maturalnego znajdziesz na poniższych stronach: