Arkusz maturalny z fizyki – poziom podstawowy – rok 2016 („stara matura”) – zadania nr 21 – 22

Na początek zapiszmy równanie soczewki w postaci ogólnej, nazywane również wzorem szlifierzy soczewek:

$$\frac{1}{f} = \left( \frac{n}{n_{osr}} \hspace{.15cm} – \hspace{.05cm} 1 \right) \left( \frac{1}{r_1} \hspace{.15cm} – \hspace{.05cm} \frac{1}{r_2} \right)$$

gdzie:
f  – ogniskowa soczewki,
n  – współczynnik załamania światła materiału soczewki,
n_osr  – współczynnik załamania światła ośrodka, z którego wnikają do soczewki promienie świetlne,
r₁  i r₂  – promienie krzywizny soczewki, przy czym r₁  to promień krzywizny powierzchni załamującej soczewki znajdującej się bliżej przedmiotu, z kolei r₂  – promień krzywizny drugiej powierzchni załamującej soczewki.

Znaki dla promieni krzywizny dobieramy w następujący sposób:
– gdy przedmiot znajduje się przed wypukłą powierzchnią załamującą soczewki, promień krzywizny r  przyjmujemy za dodatni,
– gdy przedmiot znajduje się przed wklęsłą powierzchnią załamującą soczewki, promień krzywizny r  przyjmujemy za ujemny.

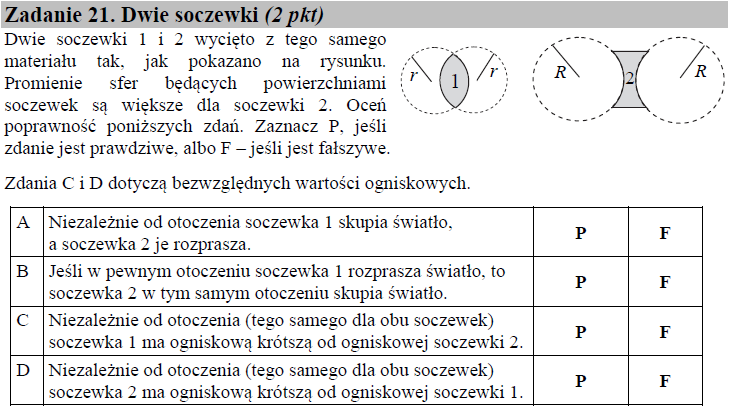
Wiemy, że r₁  = r₂  = r   i  R₁  = R₂  = R  oraz, że r  < R. Zgodnie z tymi informacjami równanie soczewki dla pierwszej, dwuwypukłej soczewki będzie równe:

$$\frac{1}{f} = \left( \frac{n}{n_{osr}} \hspace{.15cm} – \hspace{.05cm} 1 \right) \left( \frac{1}{r} + \frac{1}{r} \right) = \left( \frac{n}{n_{osr}} \hspace{.15cm} – \hspace{.05cm} 1 \right) \frac{2}{r}$$

Dodatnia wartość ogniskowej oznacza, że soczewka ma rzeczywiste ognisko (znajdujące się po przeciwnej stronie niż przedmiot), a więc jest ona soczewką skupiającą promienie świetlne.

Dla drugiej, dwuwklęsłej soczewki:

$$\frac{1}{f} = \left( \frac{n}{n_{osr}} \hspace{.15cm} – \hspace{.05cm} 1 \right) \left( \hspace{.15cm} – \hspace{.05cm} \frac{1}{R} \hspace{.15cm} – \hspace{.05cm} \frac{1}{R} \right) = \hspace{.15cm} – \hspace{.05cm} \left( \frac{n}{n_{osr}} \hspace{.15cm} – \hspace{.05cm} 1 \right) \frac{2}{R} \hspace{1cm} \longrightarrow \hspace{1cm} \hspace{.15cm} – \hspace{.05cm} \frac{1}{f} = \left( \frac{n}{n_{osr}} \hspace{.15cm} – \hspace{.05cm} 1 \right) \frac{2}{R}$$

Ujemna wartość ogniskowej oznacza, że soczewka ma pozorne ognisko (znajdujące się po tej samej stronie co przedmiot), a więc jest ona soczewką rozpraszającą promienie świetlne.

Zdanie A i B

W normalnych warunkach tj. gdy ośrodkiem, w którym rozchodzą się i z którego wnikają do soczewki promienie świetlne jest powietrze (n_osr ≅ 1), soczewka 1 jest soczewką skupiającą, a soczewka 2 – soczewką rozpraszającą. Jest tak dlatego, ponieważ wyrażenie (n/n_osr – 1) > 0 – dla tego przypadku równania soczewki dla soczewki 1 i 2 będą dokładnie takie, jak zapisano powyżej. W sytuacji, gdy n_osr > n, wyrażenie (n/n_osr – 1) < 0, w związku z czym soczewka 1 będzie mieć ujemną ogniskową i tym samym będzie rozpraszać światło, a soczewka 2 będzie mieć dodatnią ogniskową i w konsekwencji będzie skupiać światło. Tak więc zdanie A jest fałszywe, z kolei zdanie B – prawdziwe.

Zdanie C i D

Tu sytuacja jest prosta. Wartość ogniskowej soczewki nie zależy od otoczenia. Porównaj równania soczewki dla soczewki 1 i 2. Wzory te różnią się znakiem oraz wielkością promienia krzywizny. Wiemy, że R  > r. Ogniskowa soczewki, jak i promień krzywizny występują w mianowniku, dlatego im większy promień krzywizny tym większa jest długość ogniskowej. W związku z tym faktem, soczewka 1 ma ogniskową krótszą od soczewki 2. Zdanie C – prawdziwe, zdanie D – fałszywe.

Prawidłowa odpowiedź: A – F,   B – P,   C – P,   D – F.

Jednym z faktów obserwacyjnych potwierdzającym hipotezę Wielkiego Wybuchu jest występowanie mikrofalowego promieniowania tła (tzw. promieniowania reliktowego), które według wielu źródeł pochodzi z okresu około 380 tysięcy lat po wystąpieniu Wielkiego Wybuchu. Drugim z faktów jest przesunięcie ku czerwieni widma promieniowania elektromagnetycznego pochodzącego np. z odległych galaktyk – zjawisko to jest przejawem ekspansji (rozszerzania się) Wszechświata.

Prawidłowa odpowiedź: mikrofalowe promieniowanie tła, przesunięcie ku czerwieni.

Rozwiązania kolejnych zadań z tego arkusza maturalnego znajdziesz na poniższych stronach: