Arkusz maturalny z fizyki – poziom podstawowy – rok 2016 („stara matura”) – zadania nr 16 – 20

a) Przepływ prądu w obwodzie spowodowany jest wybiciem elektronów z powierzchni płytki. Zjawisko to, po raz pierwszy opisane przez Alberta Einsteina, nosi nazwę zjawiska fotoelektrycznego zewnętrznego. Emisja elektronów z powierzchni płytki zachodzi tylko wtedy, gdy energia fotonów (kwantów promieniowania elektromagnetycznego) padających na płytkę równa jest co najmniej pracy wyjścia elektronów z płytki. Praca wyjścia to wielkość charakteryzująca dany materiał równa najmniejszej energii, jaką należy dostarczyć elektronowi, aby opuścił on powierzchnię płytki i stał się elektronem swobodnym.
b) Umowny kierunek przepływu prądu elektrycznego odbywa się od bieguna o wyższym potencjale (biegunie dodatnim) do bieguna o niższym potencjale (biegunie ujemnym). Umowa ta jest prawdziwa dla nośników obdarzonych ładunkiem dodatnim. W przypadku metali, w których nośnikami prądu są ujemnie naładowane elektrony swobodne, kierunek przepływu prądu odbywa się w kierunku przeciwnym, czyli od bieguna ujemnego do bieguna dodatniego. Zgodnie z rysunkiem do bieguna ujemnego źródła napięcia podłączona jest płytka P, zatem to elektrony wybite z powierzchni tej płytki spowodują wychylenie wskazówki mikroamperomierza.
Prawidłowa odpowiedź: a) zjawisko fotoelektryczne zewnętrzne, b) płytka P.

Wielkością szukaną jest maksymalna długość fali promieniowania elektromagnetycznego, nazywana również długością graniczną fali, która może spowodować przepływ prądu elektrycznego w obwodzie. Maksymalnej długości fali odpowiada minimalna energia, jaką musi posiadać foton, aby spowodować wystąpienie zjawiska fotoelektrycznego zewnętrznego. Zasadę zachowania energii dla tego zjawiska opisuje poniższe równanie:
$$E_f = W + E_k$$
gdzie:
Ef – energia fotonu,
W – praca wyjścia elektronu z płytki,
Ek – energia kinetyczna wybitego elektronu.
Zgodnie z informacją zamieszczoną wyżej, energia fotonu o granicznej długości fali równa jest dokładnie pracy wyjścia elektronu z powierzchni płytki (szukamy minimalnej energii fotonu, a więc energia kinetyczna fotonu musi być równa zero), w związku z czym:
$$E_f = W$$
Ponieważ energia fotonu jest równa:
$$E_f = h \hspace{.05cm} \nu = h \hspace{.05cm} \frac{c}{\lambda}$$
gdzie:
h – stała Plancka równa 6,626 ⋅ 10-34 J ⋅ s,
ν – częstotliwość drgań fotonu,
c – prędkość światła w próżni równa 3 ⋅ 108 m/s,
λ – długość fali fotonu,
zatem:
$$\lambda = \frac{h \hspace{.05cm} c}{E_f} = \frac{h \hspace{.05cm} c}{W} = \frac{6,\hspace{-.1cm}626 \cdot 10^{-34}
\hspace{.05cm} \textrm{J} \cdot \textrm{s} \cdot 3 \cdot 10^8 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}}}{7,\hspace{-.1cm}2 \cdot 10^{-19} \hspace{.05cm} \textrm{J}} = 2,\hspace{-.1cm}76 \cdot 10^{-7} \hspace{.05cm} \textrm{m} = 276 \hspace{.05cm} \textrm{nm}$$
Prawidłowa odpowiedź: maksymalna długość fali fotonu wynosi λ = 276 nm.
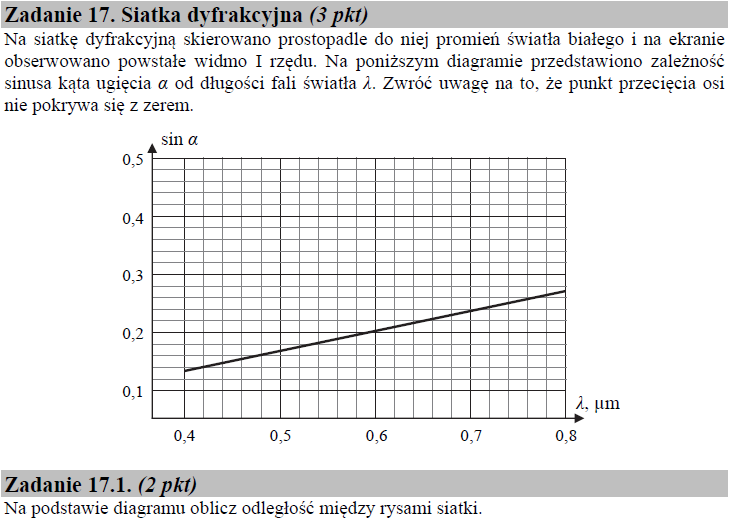
Odległość między rysami (szczelinami) siatki dyfrakcyjnej to tzw. stała siatki dyfrakcyjnej, oznaczana literą d. Białe światło padające na siatkę dyfrakcyjną ulega rozłożeniu na fale składowe, widoczne na ekranie w postaci widma. Widmo to składa się z szeregu linii, których położenie na ekranie związane jest z kątem α ugięcia fali na szczelinie. Związek między stałą siatki d, kątem ugięcia α i długością λ fali światła oraz rzędem widma n wyraża poniższe równanie:
$$d \hspace{.05cm} \textrm{sin} \hspace{.05cm} \alpha = n \hspace{.05cm} \lambda$$
(rząd widma to liczba przypisana każdej linii widmowej określająca jej pozycję w stosunku do linii centralnej widma).
Po przekształceniu powyższego wzoru względem stałej siatki d, dostaniemy:
$$d = \frac{n \hspace{.05cm} \lambda}{\textrm{sin} \hspace{.05cm} \alpha}$$
Wykres przedstawia zależność sinusa kąta ugięcia α od długości λ fali światła dla widma pierwszego rzędu, w związku z czym n = 1. Aby obliczyć stałą siatki wybierzmy współrzędne jednego z punktów leżących na wykresie np. λ = 0,5 μm, sin α = 0,17 i dokonajmy obliczeń:
$$d = \frac{0,\hspace{-.1cm}5 \hspace{.05cm} \mu\textrm{m}}{0,\hspace{-.1cm}17} = 2,\hspace{-.1cm}94 \hspace{.05cm} \mu\textrm{m} \cong 3,\hspace{-.1cm}0 \hspace{.05cm} \mu\textrm{m}$$
Prawidłowa odpowiedź: d ≅ 3,0 μm.

Dla widma drugiego rzędu n = 2, w związku z czym:
$$\textrm{sin} \hspace{.05cm} \alpha = \frac{2 \hspace{.05cm} \lambda}{d}$$
Stałą siatki znamy. Długości fal, dla których mamy obliczyć sinus kąta ugięcia mamy podane na wykresie. Dokonajmy więc obliczeń:
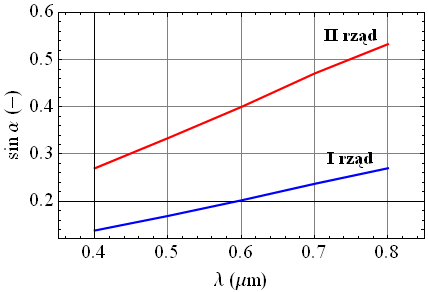
| Długość fali λ (μm) | sin α |
|---|---|
| 0,4 | 0,27 |
| 0,5 | 0,33 |
| 0,6 | 0,40 |
| 0,7 | 0,47 |
| 0,8 | 0,53 |
i narysujmy zależność sin α ( λ) :

Odpowiedzi znajdziesz w artykule Zasady termodynamiki pod hasłem Druga zasada termodynamiki.
Prawidłowa odpowiedź: 1 – poprawne, 2 – błędne, 3 – poprawne.

Wielkością szukaną jest wartość energii, jaką uzyskamy z rozszczepienia jąder uranu 235U zawartych w próbce wzbogaconego uranu o masie 1 kg. Wiemy, że uran wzbogacony zawiera 4% izotopu 235U, w związku z czym masa m tego izotopu wynosi m = 4% ⋅ 1 kg = 40 g. Następnie obliczmy ilość jąder uranu odpowiadających tej masie. Wiemy, że 1 mol 235U = 235 g, dlatego:
$$n = \frac{40 \hspace{.05cm} \textrm{g}}{235 \hspace{.05cm} \textrm{g}} \cdot 1 \hspace{.05cm} \textrm{mol} = 0,\hspace{-.1cm}17 \hspace{.05cm} \textrm{mol}$$
gdzie n to liczba jąder uranu wyrażona w molach.
Korzystając z definicji mola:
$$n = \frac{N}{N_A}$$
gdzie:
N – liczba jąder uranu,
NA – stała Avogadra równa NA = 6,023 ⋅ 1023 $\rm \frac{1}{mol}$,
otrzymamy liczbę jąder uranu równą:
$$N = n \cdot N_A = 0,\hspace{-.1cm}17 \hspace{.05cm} \textrm{mol} \cdot 6,\hspace{-.1cm}023 \cdot 10^{23} \hspace{.05cm} \tfrac{1}{\textrm{mol}} = 1,\hspace{-.1cm}02 \cdot 10^{23}$$
Energia rozszczepienia jednego jądra uranu 235U wynosi 207 MeV. Energia pochodząca z rozszczepienia 1,02 ⋅ 1023 jąder wyniesie:
$$E = 1,\hspace{-.1cm}02 \cdot 10^{23} \cdot 207 \hspace{.05cm} \textrm{MeV} = 211,\hspace{-.1cm}14 \cdot 10^{23} \hspace{.05cm} \textrm{MeV} = 211,\hspace{-.1cm}14 \cdot 10^{29} \hspace{.05cm} \textrm{eV}$$
Korzystając z faktu, że 1 eV = 1,6 ⋅ 10-19 J, dostaniemy:
$$E = 211,\hspace{-.1cm}14 \cdot 10^{29} \cdot 1,\hspace{-.1cm}6 \cdot 10^{-19} \hspace{.05cm} \textrm{J} = 338 \cdot 10^{10} \hspace{.05cm} \textrm{J}$$
Aby uzyskać taką energię ze spalania węgla należałoby zużyć:
$$m_C = \frac{E}{E_C} = \frac{338 \cdot 10^{10} \hspace{.05cm} \textrm{J}}{2 \cdot 10^7 \hspace{.05cm} \textrm{J}} = 1,\hspace{-.1cm}69 \cdot 10^5 \hspace{.05cm} \textrm{kg} = 169 \hspace{.05cm} \textrm{t}$$
Prawidłowa odpowiedź: energia z rozszczepienia 1 kg wzbogaconego uranu wyniesie E = 338 ⋅ 1010J – odpowiada to energii pochodzącej ze spalenia 169 ton węgla.

Suma liczb masowych A i liczb atomowych Z substratów reakcji musi być równa sumie liczb masowych i atomowych produktów reakcji. Dokonajmy zatem bilansu reakcji:
– suma liczb masowych przed reakcją: As = 10 + 4 = 14,
– suma liczb masowych po reakcji: Ap = 13,
– suma liczb atomowych przed reakcją: Zs = 5 + 2 = 7,
– suma liczb atomowych po reakcji: Zp = 7.
Zs = Zp, wobec czego liczba protonów substratów równa jest liczbie protonów produktów reakcji.
As > Ap, w związku z czym po reakcji „brakuje” nam jednego neutronu (liczba masowa jest sumą protonów i neutronów zgromadzonych w jądrze atomowym). Oznacza to, że $\rm X = \hspace{.05cm} ^1_0 n$.
Prawidłowa odpowiedź: neutron.
Rozwiązania kolejnych zadań z tego arkusza maturalnego znajdziesz na poniższych stronach:
Arkusz maturalny z fizyki – poziom podstawowy – rok 2016 – zadania nr 1 – 5
Arkusz maturalny z fizyki – poziom podstawowy – rok 2016 – zadania nr 6 – 10
Arkusz maturalny z fizyki – poziom podstawowy – rok 2016 – zadania nr 11 – 15
Arkusz maturalny z fizyki – poziom podstawowy – rok 2016 – zadania nr 21 – 22

Dodaj komentarz