Test: Ruch harmoniczny – poziom średni

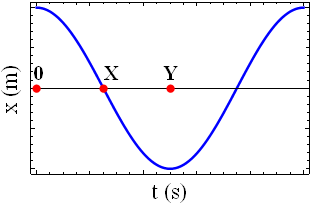
Znamy częstotliwość drgań ciała, więc z łatwością możemy obliczyć okres jednego pełnego drgania:

$$T = \frac{1}{f} = \frac{1}{50 \hspace{.05cm} \textrm{Hz}} = 0,\hspace{-.1cm}02 \hspace{.05cm} \textrm{s} = 20 \hspace{.05cm} \textrm{ms}$$

Teraz wystarczy z rysunku odczytać miejsce przecięcia wykresu z punktem X oraz Y na osi czasu i dokonać stosownych obliczeń.

Aby obliczyć częstotliwość drgań ciężarka należy rozpatrzyć dwa zdarzenia: jedno, gdy ciężarek znajduje się w położeniu równowagi, drugie, gdy ciężarek znajduje się w skrajnym położeniu tj. gdy wychylenie ciężarka odpowiada amplitudzie drgań (x  = A ). Dla pierwszego przypadku dostaniemy:

$$x (t = 0 \hspace{.05cm} \textrm{s}) = 0 \hspace{.05cm} \textrm{m} = A \hspace{.05cm} \textrm{sin} \left( \omega \cdot 0 \hspace{.05cm} \textrm{s} + \varphi \right) = A \hspace{.05cm} \textrm{sin} \varphi$$

Warunek  $\textrm{sin} \hspace{.03cm} \varphi = 0$  spełnia  $\varphi = 0$.

Dla drugiego przypadku otrzymamy:

$$x(t = 0,\hspace{-.1cm}1 \hspace{.05cm} \textrm{s}) = A = A \hspace{.05cm} \textrm{sin} \left( \omega \cdot 0,\hspace{-.1cm}1 \hspace{.05cm} \textrm{s} + \varphi \right) = A \hspace{.05cm} \textrm{sin} \left( 0,\hspace{-.1cm}2 \hspace{.05cm} \pi \hspace{.05cm} f \right)$$

Po skróceniu:

$$\textrm{sin} \left( 0,\hspace{-.1cm}2 \hspace{.05cm} \pi \hspace{.05cm} f \right) = 1$$

Warunek ten spełniony jest wtedy, gdy wyrażenie:

$$0,\hspace{-.1cm}2 \hspace{.05cm} \pi \hspace{.05cm} f = \frac{\pi}{2}$$

co oznacza, że szukana wartość częstotliwości f  = 2,5 Hz.

W punkcie maksymalnego wychylenia ciała z położenia równowagi prędkość ciała wynosi 0 m/s, a przyspieszenie przyjmuje maksymalną wartość (zobacz prędkość i przyspieszenie w ruchu harmonicznym). Korzystając ze wzoru:

$$a (t) = \hspace{.1cm} - \hspace{.05cm} \omega^2 \hspace{.05cm} x (t)$$

otrzymamy:  $a = \hspace{.1cm} - \hspace{.05cm} \omega^2 \hspace{.05cm} A$.  Wiedząc, że  $\omega = \frac{2 \hspace{.05cm} \pi}{T}$,  dostaniemy:

$$a = \hspace{.1cm} - \hspace{.05cm} \frac{4 \hspace{.05cm} \pi^2 \hspace{.05cm} A}{T^2} \approx \hspace{.1cm} - \hspace{.05cm} 5 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2}$$

(maksymalna wartość przyspieszenia zmienia się w zakresie  $\pm 5 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2}$)

Zobacz prędkość i przyspieszenie w ruchu harmonicznym - zadanie nr 4.

Siła działająca na ciało drgające ruchem harmonicznym jest wprost proporcjonalna i przeciwnie skierowana do wychylenia ciała (zobacz siła w ruchu harmonicznym). Oznacza to, że zależność pomiędzy wychyleniem x  ciała a siłą F  ma charakter liniowy (wykres jest linią prostą). Gdy x  = 0 m, siła F  = 0 N; gdy x  = A, siła F  = - k A . Gdy x  = - A , siła F  = k A . Warunki te spełnia tylko wykres a).

Zacznijmy od zapisania związku łączącego wychylenie i przyspieszenie ciała drgającego ruchem harmonicznym (zobacz prędkość i przyspieszenie w ruchu harmonicznym):

$$a(t) = \hspace{.1cm} - \hspace{.05cm} \omega^2 \hspace{.05cm} x (t)$$

Następnie wprowadźmy oznaczenia: a₁, x₁ oraz a₂, x₂, gdzie x₂ to szukane wychylenie ciała, dla którego przyspieszenie a₂ = 4 m/s². Po wprowadzeniu oznaczeń do powyższego wzoru, dostaniemy:

$$a_1 = \hspace{.1cm} - \hspace{.05cm} \omega^2 \hspace{.05cm} x_1$$

oraz:

$$a_2 = \hspace{.1cm} - \hspace{.05cm} \omega^2 \hspace{.05cm} x_2$$

Z pierwszego równania mamy:

$$\hspace{.1cm} - \hspace{.05cm} \omega^2 = \frac{a_1}{x_1}$$

Po wstawieniu tej zależności do drugiego równania oraz wykonaniu przekształceń względem x₂, otrzymamy:

$$x_2 = \frac{a_2}{a_1} \hspace{.05cm} x_1 = 6 \hspace{.05cm} \textrm{cm}$$

Korzystamy z zależności (zobacz prędkość i przyspieszenie w ruchu harmonicznym):

$$a (t) = \hspace{.1cm} - \hspace{.05cm} \omega^2 \hspace{.05cm} x (t)$$

W punkcie maksymalnego wychylenia ciała, odpowiadającego amplitudzie drgań A, przyspieszenie drgań osiąga maksymalną wartość, dlatego też:

$$a_{max} = \hspace{.1cm} - \hspace{.05cm} \omega^2 \hspace{.05cm} A$$

Częstość kołowa ω nie jest znana, lecz możemy ją powiązać z amplitudą A  oraz prędkością maksymalną V_max. Prędkość maksymalna drgań osiągana jest wtedy, gdy  $x (t) = 0 \hspace{.05cm} \textrm{m}$, w związku z czym:

$$0 = A \hspace{.05cm} \textrm{sin} \left( \omega \hspace{.05cm} t + \varphi \right)$$

Warunek ten spełniony jest, gdy  $\omega \hspace{.05cm} t = \hspace{-.1cm} - \hspace{.05cm} \varphi$.  Po wstawieniu tego warunku do wzoru na prędkość:

$$V_{max} = \omega \hspace{.05cm} A \hspace{.05cm} \textrm{cos} \left( \omega \hspace{.05cm} t + \varphi \right)$$

otrzymamy po przekształceniu:

$$\omega = \frac{V_{max}}{A}$$

Ostatecznie wzór na przyspieszenie maksymalne przyjmie następującą postać:

$$a_{max} = \hspace{-.1cm} - \hspace{.05cm} \frac{V^2_{max}}{A}$$

(znak minus możemy pominąć w obliczeniach, gdyż szukamy wartości przyspieszenia).

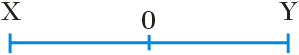
W położeniu równowagi ciało posiada maksymalną prędkość; w punktach skrajnych X i Y prędkość ciała wynosi 0 m/s. Oznacza to, że ciało na odcinku 0 - Y zwalnia. Dodatkowo wiemy, że drgania harmoniczne powodowane są przez siłę o zmiennej wartości (zobacz siła w ruchu harmonicznym), dlatego ruch ciała pomiędzy punktami 0 i Y jest ruchem niejednostajnie opóźnionym.

Wartość siły w ruchu harmonicznym zmienia się zgodnie z równaniem:

$$F (t) = \hspace{.1cm} - \hspace{.05cm} k \hspace{.05cm} x (t)$$

Maksymalna wartość siły F_max  występuje wtedy, gdy x  = A , zatem:

$$F_{max} = \hspace{.1cm} - \hspace{.05cm} k \hspace{.05cm} A$$

(znak minus informuje nas o tym, że siła jest przeciwnie skierowana do kierunku wychylenia ciała; ponieważ interesuje nas wartość siły, dlatego w kolejnych wzorach znak minus będziemy pomijać). Stałą sprężystości k  możemy powiązać z masą m  ciężarka oraz z częstością kołową ω  jego drgań:

$$k = m \hspace{.05cm} \omega^2$$

(zobacz siła w ruchu harmonicznym). Ponieważ:

$$\omega = \frac{2 \hspace{.05cm} \pi}{T}$$

dlatego:

$$F_{max} = \frac{4 \hspace{.05cm} \pi^2 \hspace{.05cm} m \hspace{.05cm} A}{T^2}$$