Arkusz maturalny z fizyki – poziom rozszerzony – rok 2017 („nowa matura”) – zadania nr 9 – 12

Sytuację opisaną w treści zadania przedstawiono poniżej:

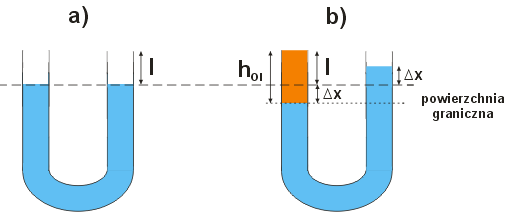
Oznaczmy szukaną maksymalną wysokość słupa oleju jako h_ol . Zgodnie z rysunkiem:

$$h_{ol} = l + \Delta \hspace{.03cm} x$$

gdzie:
l  – odległość od powierzchni słupa wody do górnego końca rurki równa 8 cm,
Δx  – zmiana wysokości słupa wody po dolaniu oleju.

Aby obliczyć h_ol  skorzystamy z warunku równowagi statycznej zgodnie, z którym ciśnienie hydrostatyczne w obydwu ramionach U-rurki na poziomie powierzchni granicznej (oznaczonej na rysunku) przyjmuje jednakową wartość (zobacz: Płyny w spoczynku, ciśnienie hydrostatyczne – zadanie nr 3):

$$p_0 + \rho_{ol} \hspace{.05cm} g \left( l + \Delta \hspace{.03cm} x \right) = p_0 + \rho_w \hspace{.05cm} g \hspace{.1cm} 2 \hspace{.05cm} \Delta \hspace{.03cm} x$$

gdzie:
p₀  – ciśnienie atmosferyczne,
g  – przyspieszenie ziemskie,
ρ_w  – gęstość wody.

Po wyeliminowaniu ciśnienia p₀  oraz po podzieleniu obydwu stron powyższego równania przez g, dostaniemy:

$$\rho_{ol} \hspace{.05cm} l + \rho_{ol} \hspace{.05cm} \Delta \hspace{.03cm} x = 2 \hspace{.05cm} \rho_w \hspace{.05cm} \Delta \hspace{.03cm} x$$

skąd mamy:

$$\rho_{ol} \hspace{.05cm} l = \Delta \hspace{.03cm} x \left( 2 \hspace{.05cm} \rho_w \hspace{.15cm} – \hspace{.05cm} \rho_{ol} \right) \hspace{1cm} \longrightarrow \hspace{1cm} \Delta \hspace{.03cm} x = \frac{\rho_{ol} \hspace{.05cm} l}{2 \hspace{.05cm} \rho_w \hspace{.15cm} – \hspace{.05cm} \rho_{ol}}$$

Po wykonaniu obliczeń otrzymamy wartość Δx  równą:

$$\Delta \hspace{.03cm} x = \frac{0,\hspace{-.1cm}82 \hspace{.05cm} \tfrac{\textrm{g}}{\textrm{cm}^3} \cdot 8 \hspace{.05cm} \textrm{cm}}{2 \cdot 1 \hspace{.05cm} \tfrac{\textrm{g}}{\textrm{cm}^3} \hspace{.15cm} – \hspace{.05cm} 0,\hspace{-.1cm}82 \hspace{.05cm} \tfrac{\textrm{g}}{\textrm{cm}^3}} = 5,\hspace{-.1cm}6 \hspace{.05cm} \textrm{cm}$$

Maksymalna wysokość słupa oleju h_ol  wynosi wobec tego:

$$h_{ol} = l + \Delta \hspace{.03cm} x = 8 \hspace{.05cm} \textrm{cm} + 5,\hspace{-.1cm}6 \hspace{.05cm} \textrm{cm} = 13,\hspace{-.1cm}6 \hspace{.05cm} \textrm{cm}$$

Prawidłowa odpowiedź: maksymalna wysokość słupa oleju h_Ol  = 13,6 cm.

Analiza rysunku: do cieczy 3 wlewamy ciecz 1. Wysokość słupa cieczy 1 w lewym ramieniu U-rurki będzie większa od wysokości słupa cieczy 3 tylko wtedy, gdy ρ₃  > ρ₁. Następnie do prawego ramienia U-rurki wlewamy ciecz 2 o gęstości ρ₂. Aby uzyskać w prawym ramieniu U-rurki takie rozmieszczenie płynów, jak na powyższym rysunku, gęstość cieczy 2 musi być mniejsza zarówno od gęstości cieczy 1, jak i 3, ponieważ tylko wtedy nacisk cieczy 2 na obydwie ciecze będzie na tyle mały, że nie wpłynie on znacząco na przesunięcie się poziomu słupa cieczy 1 i 3.

Prawidłowa odpowiedź: D.

Zacznijmy od stworzenia odpowiedniego rysunku schematycznego:

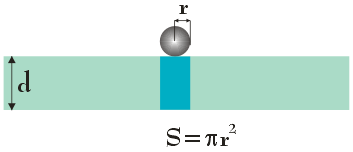
Aby kula przeszła na drugą stronę tafli musimy, zgodnie z powyższym rysunkiem, stopić lód (niebieski prostokąt) o objętości  $V_l = S \cdot d = \pi \hspace{.05cm} r^2 \hspace{.05cm} d$  (wzór na objętość walca). Wiemy, że temperatura lodu wynosi T_l  = 0 ^oC, dlatego energia cieplna rozgrzanej kulki będzie zużyta tylko i wyłącznie na stopienie lodu o objętości V_l . Równanie bilansu cieplnego dla tej sytuacji przedstawia się następująco:

$$m_k \hspace{.05cm} c_{w,st} \left( T_k \hspace{.15cm} – \hspace{.05cm} T_l \right) = m_l \hspace{.05cm} c_{T,l}$$

gdzie:
m_k  – masa kulki,
c_w,st  – ciepło właściwe stali,
T_k  – szukana minimalna temperatura kulki,
m_l  – masa lodu, który musi stopić kulka,
c_T,l  – ciepło topnienia lodu.

Ponieważ T_l  = 0^o C, dlatego:

$$m_k \hspace{.05cm} c_{w,st} \hspace{.05cm} T_k = m_l \hspace{.05cm} c_{T,l}$$

Korzystając z definicji gęstości możemy masę lodu m_l  wyrazić jako:

$$m_l = \rho_l \hspace{.05cm} V_l = \rho_l \hspace{.05cm} \pi \hspace{.05cm} r^2 \hspace{.05cm} d$$

Po przekształceniu i podstawieniu:

$$m_k \hspace{.05cm} c_{w,st} \hspace{.05cm} T_k = m_l \hspace{.05cm} c_{T,l} \hspace{1cm} \longrightarrow \hspace{1cm} T_k = \frac{m_l \hspace{.05cm} c_{T,l}}{m_k \hspace{.05cm} c_{w,st} \hspace{.05cm} T_k} = \frac{\rho_l \hspace{.05cm} V_l \hspace{.05cm} c_{T,l}}{m_k \hspace{.05cm} c_{w,st} \hspace{.05cm} T_k} = \frac{\rho_l \hspace{.05cm} \pi \hspace{.05cm} r^2 \hspace{.05cm} d \hspace{.05cm} c_{T,l}}{m_k \hspace{.05cm} c_{w,st} \hspace{.05cm} T_k}$$

oraz wykonaniu obliczeń, dostaniemy:

$$T_k = \frac{3,\hspace{-.1cm}14 \cdot \left( 2 \cdot 10^{-2} \hspace{.05cm} \textrm{m} \right)^2 \cdot 3 \cdot 10^{-2} \hspace{.05cm} \textrm{m} \cdot 900 \hspace{.05cm} \tfrac{\textrm{kg}}{\textrm{m}^3} \cdot 335000 \hspace{.05cm} \tfrac{\textrm{J}}{\textrm{kg}}}{0,\hspace{-.1cm}26 \hspace{.05cm} \textrm{kg} \cdot 460 \hspace{.05cm} \tfrac{\textrm{J}}{\textrm{kg} \hspace{.05cm} \cdot \hspace{.05cm} ^{\textrm{o}} \textrm{C}}} = 95 \hspace{.05cm} ^{\textrm{o}} \textrm{C}$$

Prawidłowa odpowiedź: minimalna temperatura kulki musi być równa T_k  = 95 ^oC.

Zdanie 1

Od długości fali padającego światła zależy położenie minimów i maksimów interferencyjnych, czyli miejsc wygaszania i wzmacniania fal, tworzących obraz interferencyjny, w związku z czym zmiana długości fali wpływa na zmianę obrazu interferencyjnego.

Zdanie 2

Odpowiedź na to pytanie zawarto powyżej. Ciemne prążki odpowiadają minimom interferencyjnym, z kolei jasne prążki – maksimom interferencyjnym.

Zdanie 3

Wraz ze zmianą odległości zwierciadła Z₂ od ekranu obraz interferencyjny ulegnie zmianie, ponieważ zmieni się droga przebywana przez promień świetlny i tym samym, podobnie jak w przypadku zmiany długości fali padającego światła, zmieni się położenie minimów i maksimów interferencyjnych.

Zdanie 4

Zmiana odległości źródła światła od płytki półprzepuszczalnej nie wpływa na zmianę obrazu interferencyjnego, ponieważ zmianie tej nie towarzyszy ani zmiana długości fali, ani zmiana dróg promieni świetlnych po przejściu przez płytkę półprzepuszczalną.

Prawidłowa odpowiedź: 1 – F,  2 – P,  3 – P,  4 – F.

Korzystamy z danych zawartych w opisie zadania. Jeden metr odpowiada 1553163,5 długości fali światła emitowanego przez lampę kadmową. Mamy zatem:

$$1553163,\hspace{-.1cm}5 \cdot \lambda = 1 \hspace{.05cm} \textrm{m} \hspace{1cm} \longrightarrow \hspace{1cm} \lambda = \frac{1 \hspace{.05cm} \textrm{m}}{1553163,\hspace{-.1cm}5} = 6,\hspace{-.1cm}44 \cdot 10^{-7} \hspace{.05cm} \textrm{m}$$

Znając długość fali λ  możemy obliczyć częstotliwość drgań światła lampy kadmowej. Korzystamy z poniższego wzoru:

$$\nu = \frac{c}{\lambda}$$

gdzie c  to prędkość światła w próżni równa 3 ⋅ 10⁸ m/s.

Po podstawieniu wartości liczbowych i wykonaniu obliczeń, dostaniemy:

$$\nu = \frac{c}{\lambda} = \frac{3 \cdot 10^8 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}}}{6,\hspace{-.1cm}44 \cdot 10^{-7} \hspace{.05cm} \textrm{m}} = 4,\hspace{-.1cm}66 \cdot 10^{14} \hspace{.05cm} \textrm{Hz}$$

Prawidłowa odpowiedź: ν  = 4,66 ⋅ 10¹⁴ Hz.

Prawidłowa odpowiedź: B – 2 i 4.

Prawidłowa odpowiedź: A.

Rozwiązania kolejnych zadań z tego arkusza maturalnego znajdziesz na poniższych stronach: