Arkusz maturalny z fizyki – poziom rozszerzony – rok 2017 („nowa matura”) – zadania nr 5 – 8

Przy założeniu stałej wartości przyspieszenia, ruch kulki po równi pochyłej możemy traktować jak ruch jednostajnie przyspieszony. Wiemy, że prędkość początkowa V₀  kuli wynosi 0 m/s, w związku z czym wzór na prędkość końcową V_k  oraz drogę s  wynosi:

$$V_k = a \hspace{.05cm} t$$

$$s = \tfrac{1}{2} \hspace{.05cm} a \hspace{.05cm} t^2$$

Po przekształceniu wzoru na drogę względem przyspieszenia a, mamy:

$$s = \tfrac{1}{2} \hspace{.05cm} a \hspace{.05cm} t^2 \hspace{1cm} \longrightarrow \hspace{1cm} a = \frac{2 \hspace{.05cm} s}{t^2}$$

Prędkość końcowa V_k  kuli wynosi zatem:

$$V_k = a \hspace{.05cm} t = \frac{2 \hspace{.05cm} s}{t^2} \cdot t = \frac{2 \hspace{.05cm} s}{t}$$

Wyprowadzenie wzoru na prędkość końcową kulki jest niepoprawne, ponieważ nie uwzględniono w nim energii kinetycznej ruchu obrotowego kuli równej  $E_{k,obr} = I \omega^2$, gdzie I  to moment bezwładności kuli, ω  – prędkość kątowa.

Prawidłowa odpowiedź: wyprowadzenie wzoru jest niepoprawne.

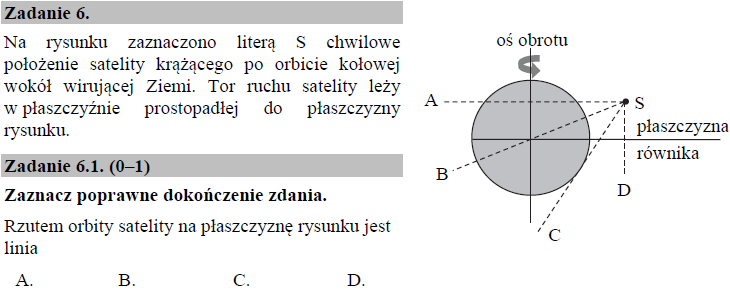
Prawidłowa odpowiedź: B.

Zdanie 1

Satelitę poruszającą się po orbicie kołowej wokół wirującej Ziemi nazywamy satelitą geostacjonarnym, gdy orbita, po której się porusza, zawiera się w płaszczyźnie równika. Satelita poruszający się po takiej orbicie zachowuje stałą pozycję nad wybranym punktem równika Ziemi. Satelita S nie może więc być satelitą geostacjonarnym, ponieważ orbita kołowa, po której się porusza nie jest, zgodnie z rysunkiem do zadania 6.1, zawarta w płaszczyźnie równika.

Zdanie 2 i 3

Aby udzielić odpowiedzi na twierdzenie 2 oraz 3 zapiszmy wzór na prędkość liniową satelity znajdującego się na wysokości h  np. nad powierzchnią Ziemi (zobacz: Prawa Keplera – zadanie nr 4):

$$V = \sqrt{\frac{\mathstrut G \hspace{.05cm} M_Z}{R_Z + h}}$$

gdzie M_Z  i R_Z  to odpowiednio masa oraz promień Ziemi.

Zwróć uwagę, że prędkość liniowa satelity nie zależy od masy satelity. Dodatkowo, wraz ze wzrostem odległości h  od powierzchni Ziemi, prędkość liniowa satelity będzie maleć (h  jest w mianowniku ułamka).

Prawidłowa odpowiedź: 1 – F,  2 – F,  3 – P.

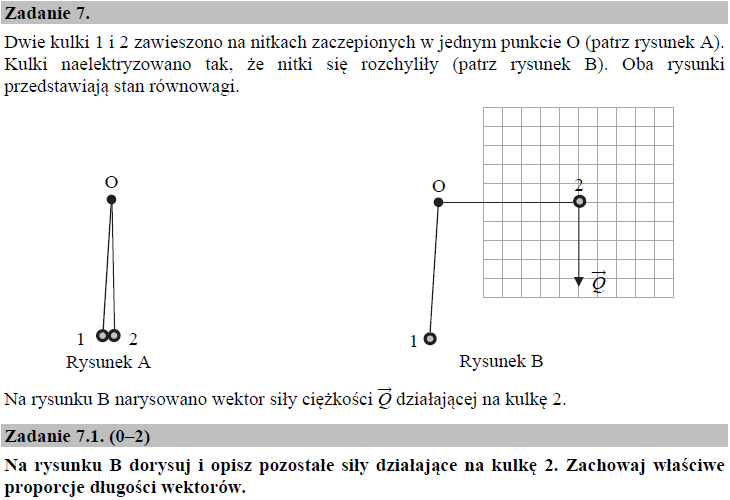
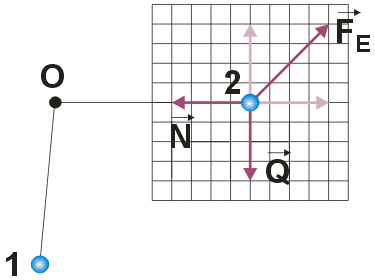
Na kulkę 2 oprócz siły ciężkości  $\vec{Q}$  działa siła oddziaływania elektrostatycznego  $\vec{F_E}$  oraz siła reakcji nici  $\vec{N}$. Kulka 2 znajduje się w położeniu równowagi, dlatego długość wektorów  $\vec{F_E}$  i  $\vec{N}$  musi być tak dobrana, aby suma sił działających na kulkę w kierunku poziomym i pionowym była równa 0. Dla większej czytelności składowe siły  $\vec{F_E}$  zostały zaznaczone na rysunku nieco jaśniejszym odcieniem koloru fioletowego:

Odchylenie obydwu, początkowo obojętnych elektrycznie, kulek spowodowała siła wzajemnego oddziaływania elektrostatycznego o charakterze odpychającym, w związku z czym kulki musiały zostać naładowane jednoimiennym ładunkiem. Stopień odchylenia obydwu kul świadczy ponadto o tym, że masa kulki 1 jest dużo większa od masy kulki 2 (gdyby kulki posiadały jednakową masę odchyliłyby się względem siebie o jednakową odległość).

Prawidłowa odpowiedź: A.

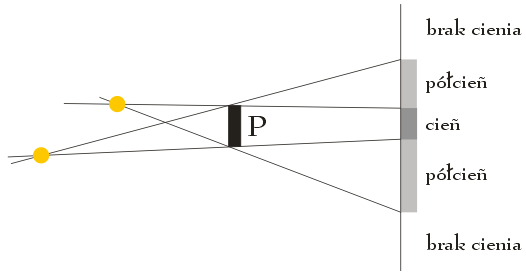
Aby konstrukcyjnie wyznaczyć położenie źródeł światła wystarczy poprowadzić cztery linie mające początek w skrajnych położeniach obszaru cienia i półcienia, styczne do krawędzi przeszkody. Punkty przecięcia się tych linii wskażą położenie źródeł światła:

Rozwiązania kolejnych zadań z tego arkusza maturalnego znajdziesz na poniższych stronach: