Arkusz maturalny z fizyki – poziom rozszerzony – rok 2017 („nowa matura”) – zadania nr 1 – 4

W zadaniu tym mamy do czynienia z ruchem jednostajnie przyspieszonym z przyspieszeniem a  < 0, ponieważ prędkość samochodu zmienia się z V₀  = 50 km/h na V_k  = 0 km/h. Aby obliczyć czas hamowania t_h  samochodu skorzystamy ze wzoru na prędkość i drogę w ruchu jednostajnie przyspieszonym (pamiętając, że a  < 0):

$$V_k = V_0 \hspace{.15cm} – \hspace{.05cm} a \hspace{.05cm} t_h$$

$$s = V_0 \hspace{.05cm} t_h \hspace{.15cm} – \hspace{.05cm} \tfrac{1}{2} \hspace{.05cm} a \hspace{.05cm} t_h^2$$

gdzie:
V₀  i V_k  to odpowiednio prędkość początkowa i końcowa samochodu,
a  – przyspieszenie samochodu,
t_h  – czas hamowania,
s  – droga hamowania.

Wielkością znaną jest s, V₀  i V_k. Przekształcając wzór na V_k  względem przyspieszenia a, dostaniemy:

$$V_k = V_0 \hspace{.15cm} – \hspace{.05cm} a \hspace{.05cm} t_h \hspace{1cm} \longrightarrow \hspace{1cm} a \hspace{.05cm} t_h = V_0 \hspace{.15cm} – \hspace{.05cm} V_k \hspace{1cm} \longrightarrow \hspace{1cm} a = \frac{V_0 \hspace{.15cm} – \hspace{.05cm} V_k}{t_h}$$

W ten sposób wyeliminowaliśmy jedną z dwóch niewiadomych. Aby obliczyć wartość t_h  podstawmy wzór na przyspieszenie a  do wzoru na drogę s :

$$s = V_0 \hspace{.05cm} t_h \hspace{.15cm} – \hspace{.05cm} \tfrac{1}{2} \hspace{.05cm} t_h^2 \cdot \left( \frac{V_0 \hspace{.15cm} – \hspace{.05cm} V_k}{t_h} \right) = V_0 \hspace{.05cm} t_h \hspace{.15cm} – \hspace{.05cm} \tfrac{1}{2} \hspace{.05cm} V_0 \hspace{.05cm} t_h + \tfrac{1}{2} \hspace{.05cm} V_k \hspace{.05cm} t_h = \tfrac{1}{2} \hspace{.05cm} V_0 \hspace{.05cm} t_h + \tfrac{1}{2} \hspace{.05cm} V_k \hspace{.05cm} t_h$$

Po przekształceniu powyższego wzoru względem t_h , otrzymamy:

$$t_h = \frac{2 \hspace{.05cm} s}{V_0 + V_k}$$

Czas hamowania samochodu mamy wyrazić w sekundach, dlatego prędkości V₀  i V_k  podane w km/h musimy wyrazić w m/s. Korzystamy z zależności:  $1 \frac{\rm m}{\rm s} = 3,\hspace{-.1cm}6 \frac{\rm km}{\rm h}$, w związku z czym  $V_0 = 13,\hspace{-.1cm}89 \frac{\rm m}{\rm s}$,  $V_k = 0 \frac{\rm m}{\rm s}$. W efekcie mamy:

$$t_h = \frac{2 \cdot 12 \hspace{.05cm} \textrm{m}}{13,\hspace{-.1cm}89 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}} + 0 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}}} = 1,\hspace{-.1cm}73 \hspace{.05cm} \textrm{s}$$

Prawidłowa odpowiedź: czas hamowania samochodu t_h  = 1,73 s.

Zdanie 1

Zjawisko tarcia jest bezpośrednio związane z niedoskonałością powierzchni, po której się poruszamy. Im większa niedoskonałość (chropowatość) powierzchni, tym większa wartość współczynnika tarcia, a więc tym większa siła tarcia działająca na poruszające się ciało.

Zdanie 2

Im większa wartość współczynnika tarcia opon o jezdnię, tym większa wartość siły tarcia działającej na poruszający się samochód i tym samym krótsza droga hamowania samochodu.

Zdanie 3

Zjawisko poślizgu wpływa bardzo niekorzystnie na ruch samochodu przyczyniając się do chwilowej lub całkowitej utraty sterowności nad samochodem. Jednym z bezpośrednich efektów poślizgu jest wydłużenie minimalnej drogi hamowania samochodu – wskutek chwilowego „braku kontaktu” opon z podłożem prędkość samochodu nie ulega zmniejszeniu wraz z pokonywaniem kolejnych odcinków jezdni.

Prawidłowa odpowiedź: 1 – P,  2 – P,  3 – P.

Podobnie jak w zadaniu 1.1 rozwiązywanie tego zadania rozpoczniemy od zapisania wzorów na prędkość V_k  i drogę s :

$$V_k = V_0 \hspace{.15cm} – \hspace{.05cm} a \hspace{.05cm} t_h$$

$$s = V_0 \hspace{.05cm} t_h \hspace{.15cm} – \hspace{.05cm} \tfrac{1}{2} \hspace{.05cm} a \hspace{.05cm} t_h^2$$

Zgodnie z treścią zadania przyspieszenie a  samochodu wynosi tyle samo, co przyspieszenie samochodu z zadania 1.1, dlatego:

$$a = \frac{13,\hspace{-.1cm}89 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}} + 0 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}}}{1,\hspace{-.1cm}73 \hspace{.05cm} \textrm{s}} = 8,\hspace{-.1cm}03 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2}$$

Ze wzoru na V_k  dostaniemy wyrażenie na t_h  równe:

$$V_k = V_0 \hspace{.15cm} – \hspace{.05cm} a \hspace{.05cm} t_h \hspace{1cm} \longrightarrow \hspace{1cm} a \hspace{.05cm} t_h = V_0 \hspace{.15cm} – \hspace{.05cm} V_k \hspace{1cm} \longrightarrow \hspace{1cm} t_h = \frac{V_0 \hspace{.15cm} – \hspace{.05cm} V_k}{a}$$

Po podstawieniu wzoru na t_h  do wzoru na drogę s, otrzymamy:

$$s = V_0 \cdot \left( \frac{V_0 \hspace{.15cm} – \hspace{.05cm} V_k}{a} \right) \hspace{.15cm} – \hspace{.05cm} \tfrac{1}{2} \hspace{.05cm} a \cdot \left( \frac{V_0 \hspace{.15cm} – \hspace{.05cm} V_k}{a} \right)^2 = \frac{V_0^2}{a} \hspace{.15cm} – \hspace{.05cm} \frac{V_0 \hspace{.05cm} V_k}{a} \hspace{.15cm} – \hspace{.05cm} \frac{1}{2 \hspace{.05cm} a} \cdot \left( V_0^2 \hspace{.15cm} – \hspace{.05cm} 2 \hspace{.05cm} V_0 \hspace{.05cm} V_k + V_k^2 \right)$$

Po skróceniu:

$$s = \frac{V_0^2}{a} \hspace{.15cm} – \hspace{.05cm} \frac{V_0 \hspace{.05cm} V_k}{a} \hspace{.15cm} – \hspace{.05cm} \frac{V_0^2}{2 \hspace{.05cm} a} + \frac{V_0 \hspace{.05cm} V_k}{a} \hspace{.15cm} – \hspace{.05cm} \frac{V_k^2}{2 \hspace{.05cm} a} = \frac{V_0^2}{2 \hspace{.05cm} a} \hspace{.15cm} – \hspace{.05cm} \frac{V_k^2}{2 \hspace{.05cm} a} = \frac{\left( V_0^2 \hspace{.15cm} – \hspace{.05cm} V_k^2 \right)}{2 \hspace{.05cm} a}$$

i przekształceniu względem V_k  dostaniemy wzór na prędkość samochodu w chwili zderzenia z przeszkodą:

$$V_k^2 = V_0^2 \hspace{.15cm} – \hspace{.05cm} 2 \hspace{.05cm} a \hspace{.05cm} s \hspace{1cm} \longrightarrow \hspace{1cm} V_k = \sqrt{\mathstrut V_0^2 \hspace{.15cm} – \hspace{.05cm} 2 \hspace{.05cm} a \hspace{.05cm} s}$$

Po podstawieniu wartości liczbowych i wykonaniu obliczeń dostaniemy (pamiętamy o zamianie jednostek prędkości:  $V_0 = 60 \frac{\rm km}{\rm h} = 16,\hspace{-.1cm}67 \frac{\rm m}{\rm s}$):

$$V_k = \sqrt{\left( \mathstrut 16,\hspace{-.1cm}67 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}} \right)^2 \hspace{.15cm} – \hspace{.05cm} 2 \cdot 8,\hspace{-.1cm}03 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2} \cdot 12 \hspace{.05cm} \textrm{m}} = 9,\hspace{-.1cm}23 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}}$$

Prawidłowa odpowiedź: prędkość samochodu w chwili uderzenia w przeszkodę V_k  = 9,23 m/s.

Aby rozłożyć wektor prędkości  $\vec{V}$  kuli K1 na składowe  $\vec{V_I}$  i  $\vec{V_{II}}$  należy poprowadzić dwie proste równoległe do osi I i II, styczne do końca wektora prędkości  $\vec{V}$.

Kierunek ruchu kuli K1 jest zgodny z kierunkiem osi II, z kolei kuli K2 – z kierunkiem osi I.

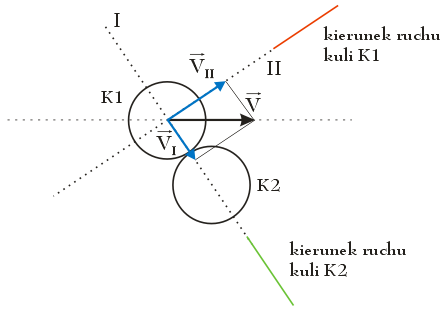
Prawidłowa odpowiedź: C.

Wyrażenie opisujące strumień indukcji pola magnetycznego $\Phi$  przedstawia się następująco:

$$\Phi = \vec{B} \cdot \vec{S} = B \hspace{.05cm} S \hspace{.05cm} \textrm{cos} \hspace{.03cm} \alpha$$

gdzie:
$\vec{B}$  – wektor indukcji pola magnetycznego,
$\vec{S}$  – wektor powierzchni S,
$\alpha$  – kąt zawarty między wektorami  $\vec{B}$  i  $\vec{S}$.

Zgodnie z treścią zadania linie pola magnetycznego ustawione są prostopadle względem ramki, w związku z czym wektory  $\vec{B}$  i  $\vec{S}$  są względem siebie równoległe ($\vec{B}$  ||  $\vec{S}$) (wektor  $\vec{S}$  związany z ramką jest ustawiony prostopadle do ramki i ma kierunek zgodny z kierunkiem wektora indukcji  $\vec{B}$ ). Dla równoległego ustawienia tychże wektorów kąt α  = 0^o.

Po podstawieniu wartości liczbowych do powyższego wzoru, otrzymamy:

$$\Phi = B \hspace{.05cm} S \hspace{.05cm} \textrm{cos} \hspace{.03cm} 0^{\textrm{o}} = 0,\hspace{-.1cm}2 \hspace{.05cm} \textrm{T} \cdot 0,\hspace{-.1cm}05 \hspace{.05cm} \textrm{m} \cdot 0,\hspace{-.1cm}1 \hspace{.05cm} \textrm{m} \cdot 1 = 0,\hspace{-.1cm}001 \hspace{.05cm} \textrm{Wb}$$

Prawidłowa odpowiedź: strumień indukcji $\Phi$  = 0,001 Wb.

Oznaczmy szukany kąt jako β, a odpowiadającą mu wartość strumienia indukcji pola magnetycznego jako  $\Phi_k$.  Z warunków zadania mamy:

$$\Phi_k = \tfrac{1}{2} \hspace{.05cm} \Phi$$

Wiemy, że:

$$\Phi_k = B \hspace{.05cm} S \hspace{.05cm} \textrm{cos} \hspace{.03cm} \beta \hspace{1cm} , \hspace{1cm} \Phi = B \hspace{.05cm} S \hspace{.05cm} \textrm{cos} \hspace{.03cm} \alpha$$

Po podstawieniu powyższych wyrażeń do wzoru  $\Phi_k = \frac{1}{2} \hspace{.05cm} \Phi$  dostaniemy (wiemy z zadania 3.1, że kąt α  = 0⁰, dla którego cos 0^o = 1):

$$B \hspace{.05cm} S \hspace{.05cm} \textrm{cos} \hspace{.03cm} \beta = \tfrac{1}{2} \cdot B \hspace{.05cm} S \hspace{.05cm} \textrm{cos} \hspace{.03cm} \alpha = \tfrac{1}{2} \hspace{.05cm} B \hspace{.05cm} S \hspace{1cm} \longrightarrow \hspace{1cm} \textrm{cos} \hspace{.03cm} \beta = \tfrac{1}{2}$$

Powyższy warunek spełnia kąt  β  = 60⁰.

Prawidłowa odpowiedź: szukany kąt wynosi 60^o.

Zgodnie z prawem indukcji Faradaya wartość siły elektromotorycznej ε  indukowanej w obwodzie zależy od szybkości zmian strumienia  $Φ$  indukcji pola magnetycznego przechodzącego przez obwód:

$$\varepsilon = \hspace{.15cm} – \hspace{.05cm} \frac{d\Phi}{dt}$$

gdzie wyrażenie  $\dfrac{d\Phi}{dt}$  opisuje wspomnianą szybkość zmiany strumienia indukcji pola magnetycznego.

Gdy w miejsce strumienia  $\Phi$  podstawimy zależność  $\Phi = B \hspace{.05cm} S \hspace{.05cm} \textrm{cos} \hspace{.03cm} \alpha$  i następnie obliczymy pochodną  $\dfrac{d\Phi}{dt}$, dostaniemy:

$$\varepsilon = \hspace{.15cm} – \hspace{.05cm} \frac{d}{dt} \left( B \hspace{.05cm} S \hspace{.05cm} \textrm{cos} \hspace{.03cm} \alpha \right) = B \hspace{.05cm} S \hspace{.05cm} \textrm{sin} \hspace{.03cm} \alpha$$

Zgodnie z powyższym wzorem największą wartość siły elektromotorycznej (i tym samym największe wskazanie woltomierza) uzyskamy dla kąta α  = 90^o, a więc dla przypadku, w którym wektor indukcji pola magnetycznego  $\vec{B}$  będzie ustawiony prostopadle do wektora powierzchni  $\vec{S}$  (innymi słowy: linie pola magnetycznego będą ustawione równolegle – pod kątem 0^o – do powierzchni ramki).

Prawidłowa odpowiedź: A – 3.

Korzystamy z drugiej zasady dynamiki Newtona oraz wzoru na drogę w ruchu jednostajnie przyspieszonym (na kamień działa stała siła ciężkości oraz stała siła oporu). Na kamień upuszczony z okna z wysokości h  działa siła ciężkości  $\vec{F_g}$  oraz stała siła oporu powietrza  $\vec{F_T}$. Mamy:

$$F_g \hspace{.15cm} – \hspace{.05cm} F_T = m \hspace{.05cm} a \hspace{1cm} \longrightarrow \hspace{1cm} m \hspace{.05cm} g \hspace{.15cm} – \hspace{.05cm} F_T = m \hspace{.05cm} a \hspace{1cm} \longrightarrow \hspace{1cm} a = \frac{m \hspace{.05cm} g \hspace{.15cm} – \hspace{.05cm} F_T}{m} = g \hspace{.15cm} – \hspace{.05cm} \frac{F_T}{m}$$

Ze wzoru na drogę w ruchu jednostajnie przyspieszonym, którą oznaczymy jako h, mamy:

$$s = h = V_0 \hspace{.05cm} t + \tfrac{1}{2} \hspace{.05cm} a \hspace{.05cm} t^2$$

Ponieważ  $V_0 = 0 \frac{\rm m}{\rm s}$, dlatego:

$$h = \tfrac{1}{2} \hspace{.05cm} a \hspace{.05cm} t^2 \hspace{1cm} \longrightarrow \hspace{1cm} t^2 = \frac{2 \hspace{.05cm} h}{a} \hspace{1cm} \longrightarrow \hspace{1cm} t = \sqrt{\frac{\mathstrut 2 \hspace{.05cm} h}{a}}$$

Po wstawieniu w miejsce a  wyrażenia  $a = g \hspace{.15cm} – \hspace{.05cm} \frac{F_T}{m}$, dostaniemy:

$$t = \sqrt{\frac{\mathstrut 2 \hspace{.05cm} h}{g \hspace{.15cm} – \hspace{.05cm} \dfrac{F_T}{m}}} = \sqrt{\frac{\mathstrut 2 \cdot 19,\hspace{-.1cm}4 \hspace{.05cm} \textrm{m}}{9,\hspace{-.1cm}81 \hspace{.05cm} \tfrac{\textrm{m}}{\textrm{s}^2} \hspace{.15cm} – \hspace{.05cm} \dfrac{0,\hspace{-.1cm}148 \hspace{.05cm} \textrm{N}}{0,\hspace{-.1cm}255 \hspace{.05cm} \textrm{kg}}}} = 2,\hspace{-.1cm}05 \hspace{.05cm} \textrm{s}$$

Prawidłowa odpowiedź: przyjęty model zjawiska poprawnie opisuje zaistniałą sytuację.

Siła oporu powietrza jest wprost proporcjonalna do kwadratu prędkości poruszającego się ciała, dlatego tuż przed upadkiem kamienia na ziemię, wartość siły oporu F_T  będzie większa od wartości 0,148 N.

Prawidłowa odpowiedź: B – 1.

Rozwiązania kolejnych zadań z tego arkusza maturalnego znajdziesz na poniższych stronach: