Test: Prąd elektryczny – poziom łatwy
Poniższy rysunek przedstawia prosty obwód elektryczny składający się z dwóch idealnych źródeł SEM oraz dwóch rezystorów. Przez oporniki R1 i R2 płyną prądy:
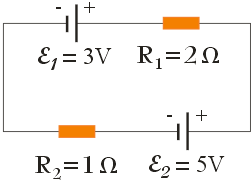
Korzystamy z drugiego prawa Kirchhoffa. Wszystkie elementy obwodu połączone są szeregowo, zatem przez rezystory przepływa prąd o jednakowym natężeniu. Kierunek przepływu prądu w obwodzie wyznaczony jest przez źródło o większej wartości SEM (źródło ε2), w związku z czym odbywa się on przeciwnie do ruchu wskazówek zegara. Drugie prawo Kirchhoffa zastosowane do tego obwodu wynosi:
$$\varepsilon_2 \hspace{.15cm} - \hspace{.05cm} I \hspace{.05cm} R_1 \hspace{.15cm} - \hspace{.05cm} \varepsilon_1 \hspace{.15cm} - \hspace{.05cm} I \hspace{.05cm} R_2 = 0$$Po przekształceniu tego wyrażenia względem prądu I, dostaniemy:
$$I = \frac{\varepsilon_2 \hspace{.15cm} - \hspace{.05cm} \varepsilon_1}{R_1 + R_2} = \tfrac{2}{3} \hspace{.05cm} \textrm{A}$$Trzy jednakowe opory o wartości 4 Ω połączono równolegle. Opór zastępczy oporników wynosi:
Zobacz równoległe łączenie rezystorów.
Trzy żarówki o mocach 100 W, 250 W i 500 W są przystosowane do pracy przy napięciu 230 V. Stosunek ich oporów (w temperaturach pracy) wynosi:
Korzystamy ze wzoru na opór $R = \frac{U}{I}$ oraz moc prądu elektrycznego $P = U \hspace{.05cm} I$. Wielkością szukaną jest opór R, zatem:
$$R = \frac{U}{I} = \frac{U^2}{P}$$Po podstawieniu do powyższego wzoru wartości liczbowych i wykonaniu obliczeń dostaniemy szukany stosunek oporów równy 1:0,4:0,2.
Trzy jednakowe opory o wartości 3 Ω połączono szeregowo. Opór zastępczy oporników wynosi:
Zobacz szeregowe łączenie rezystorów.
Dwa przewody wykonano z jednakowego materiału, przy czym jeden z nich jest dwa razy dłuższy od drugiego. Opór dłuższego przewodu w porównaniu z przewodem krótszym jest:
Opór R krótszego przewodu jest równy $R_k = \rho \hspace{.05cm} \frac{l}{S}$, z kolei dłuższego $R_d = \rho \hspace{.05cm} \frac{2 \hspace{.05cm} l}{S}$. Po podzieleniu Rd przez Rk , dostaniemy:
$$\frac{R_d}{R_k} = \frac{2 \hspace{.05cm} \rho \hspace{.05cm} l \hspace{.05cm} S}{\rho \hspace{.05cm} l \hspace{.05cm} S} = 2$$Poniższy rysunek przedstawia prosty obwód elektryczny składający się z dwóch idealnych źródeł SEM oraz dwóch rezystorów. Potencjał w punkcie A, B i C wynosi odpowiednio:
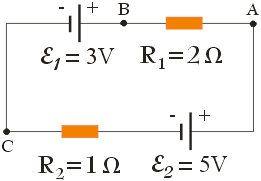
Aby wyznaczyć natężenie prądu przepływającego przez obwód skorzystamy z drugiego prawa Kirchhoffa:
$$\varepsilon_2 \hspace{.15cm} - \hspace{.05cm} I \hspace{.05cm} R_1 \hspace{.15cm} - \hspace{.05cm} \varepsilon_1 \hspace{.15cm} - \hspace{.05cm} I \hspace{.05cm} R_2 = 0$$Po przekształceniu powyższego wzoru względem I, otrzymamy:
$$I = \frac{\varepsilon_2 \hspace{.15cm} - \hspace{.05cm} \varepsilon_1}{R_1 + R_2} = \tfrac{2}{3} \hspace{.05cm} \textrm{A}$$Znając prąd możemy przystąpić do wyznaczenia potencjałów. Potencjał w punkcie A jest równy SEM źródła ε2, więc VA = 5 V. Potencjał w punkcie B jest pomniejszony o spadek napięcia na rezystorze R1:
$$U_1 = I \hspace{.05cm} R_1 = \tfrac{4}{3} \hspace{.05cm} \textrm{V}$$więc:
$$V_B = 5 \hspace{.05cm} \textrm{V} \hspace{.15cm} - \hspace{.05cm} \tfrac{4}{3} \hspace{.05cm} \textrm{V} = 3 \tfrac{2}{3} \hspace{.05cm} \textrm{V}$$Potencjał w punkcie C pomniejszony jest o spadek na źródle ε1, zatem:
$$V_C = V_B \hspace{.15cm} - \hspace{.05cm} \varepsilon_1 = 3 \tfrac{2}{3} \hspace{.05cm} \textrm{V} \hspace{.1cm} - \hspace{.05cm} 3 \hspace{.05cm} \textrm{V} = \tfrac{2}{3} \hspace{.05cm} \textrm{V}$$Zwiększając ilość rzeczywistych ogniw połączonych szeregowo powodujemy, że:
Odbiornik o oporze 20 Ω pobiera w ciągu 0,5 h 1 kWh energii elektrycznej. Oznacza to, że natężenie prądu wynosi:
Praca wykonywana przez prąd elektryczny wynosi $W = U \hspace{.05cm} I \hspace{.05cm} t$. Ponieważ praca jest rodzajem energii, zatem energię E pobieraną przez odbiornik możemy wyrazić jako $E = U \hspace{.05cm} I \hspace{.05cm} t$. Korzystając z definicji oporu elektrycznego $R = \frac{U}{I}$, otrzymamy: $E = I^2 \hspace{.05cm} R \hspace{.05cm} t$, skąd po przekształceniu względem I, dostaniemy:
$$I = \sqrt{\frac{\mathstrut E}{R \hspace{.05cm} t}}$$Po wyrażeniu energii w J (1kWh = 3 600 000 J) oraz czasu w sekundach (0,5 h = 1800 s) otrzymamy szukaną wartość natężenia prądu równą I = 10 A.
Przewód o oporze R przecięto w połowie długości i otrzymane części połączono równolegle. Opór tak otrzymanego przewodnika wynosi:
Opór R dowolnego przewodnika możemy wyrazić wzorem $R = \rho \hspace{.05cm} \frac{l}{S}$, gdzie ρ - opór właściwy, l - długość, S - pole przekroju poprzecznego przewodnika. Po przecięciu przewodnika na dwie równe połowy, opór każdej części będzie równy $R = \rho \hspace{.05cm} \frac{0,5 \hspace{.05cm} l}{S}$. Po podstawieniu tych oporów do wyrażenia pozwalającego obliczyć opór zastępczy oporników połączonych równolegle dostaniemy, że:
$$R_z = \tfrac{1}{4} \hspace{.05cm} \rho \hspace{.05cm} \tfrac{l}{S} = \tfrac{1}{4} \hspace{.05cm} R$$Aby wyznaczyć opór właściwy dowolnego przewodnika musimy dysponować źródłem napięcia, woltomierzem, amperomierzem oraz:
Przekształcając wyrażenie $R = \rho \hspace{.05cm} \frac{l}{S}$ względem oporu właściwego ρ, dostaniemy:
$$\rho = \frac{R \hspace{.05cm} S}{l}$$Korzystając z definicji oporu $R = U \hspace{.05cm} I$, otrzymamy:
$$\rho = \frac{U \hspace{.05cm} S}{l \hspace{.05cm} I}$$Brakującymi przyrządami są więc przymiar metrowy do wyznaczenia długości l oraz śruba mikrometryczna do wyznaczenia pola przekroju poprzecznego S przewodnika.

1 komentarz
Małgorzata
Dodano dnia 14 stycznia 2020 o godz. 20:32
Dobry test