Test: Mechanika płynów – poziom średni

Aby obliczyć maksymalny ciężar jaki może unieść większy tłok prasy hydraulicznej skorzystamy z prawa Pascala. Zgodnie z tym prawem zmiana ciśnienia przenoszona jest bez zmiany wartości do każdego miejsca w płynie oraz do ścianek zbiornika. W naszym przypadku zmiana ciśnienia spowodowana naciskiem mniejszego tłoka przenoszona jest bez zmiany wartości do tłoka większego. Korzystając z tego faktu oraz definicji ciśnienia możemy zapisać, że  $\frac{F_1}{S_1} = \frac{F_2}{S_2}$.  Po wykonaniu przekształceń oraz obliczeń dostaniemy szukaną wartość siły F₂ .

Aby obliczyć stosunek ciśnień wywieranych przez wodę na dno obydwu szklanek należy skorzystać ze wzoru na ciśnienie hydrostatyczne. Wysokość cieczy w szklankach możemy wyrazić poprzez objętość oraz pole podstawy szklanki (korzystamy ze wzoru na objętość walca). Objętość wody jest jednakowa w obydwu szklankach. Pola podstawy są różne. Po podstawieniu ich do wzoru i wykonaniu obliczeń dostaniemy szukaną wartość stosunku ciśnień hydrostatycznych.

Ciężar kawałka metalu zmierzony w wodzie oraz w nieznanej cieczy jest jego ciężarem pozornym. Korzystając z definicji ciężaru pozornego, możemy dla pierwszego przypadku, czyli przypadku, w którym metal znajduje się w wodzie, wyznaczyć objętość wody wypartej przez metal. Ponieważ metal całkowicie zanurzony jest w wodzie, dlatego też objętość ta musi być równa objętości metalu. Zapisując podobne równanie na ciężar pozorny ciała dla drugiego przypadku i wstawiając w miejsce objętości nieznanej cieczy objętość wyznaczoną z pierwszego przypadku dostaniemy szukaną gęstość cieczy.

Gdy łódka pływa po basenie częściowo wynurzona, siła wyporu równoważy siłę ciężkości łódki oraz przedmiotu znajdującego się na jej powierzchni. Jeżeli ciało wyrzucone z łódki ma gęstość większą od gęstości wody, ciało to opadnie oczywiście na dno basenu. Taka sytuacja spowoduje, że siła wyporu działająca na ciało znajdujące się na dnie basenu będzie mniejsza od siły ciężkości i w związku z tym poziom wody, ze względu na zmianę objętości wypartej wody, ulegnie zmianie (nieco opadnie). Zjawisko to dotyczy kamienia, wiosła oraz beczki soli. Koło ratunkowe po wyrzuceniu z łódki będzie pływać po powierzchni basenu - siłę ciężkości łódki i koła będzie równoważyć siła wyporu o takiej samej wartości - zatem poziom wody w basenie nie ulegnie zmianie.

Odczytaj z wykresu dla ustalonego przez siebie punktu wartość ciśnienia oraz głębokości i skorzystaj następnie ze wzoru na ciśnienie hydrostatyczne.

Zgodnie z prawem Archimedesa ciało o gęstości mniejszej niż gęstość płynu, w którym jest zanurzone, pływa. Gęstość lodu wynosi 900 kg/m³, gęstość wody - 1000 kg/m³. Oznacza to, że 1/10 objętości góry lodowej unosi się nad powierzchnią wody, z kolei 9/10 góry znajduje się tuż pod powierzchnią wody. Dzieląc te dwie wielkości przez siebie otrzymamy szukany ułamek równy 1/9.

Klocek pływa, a więc siła wyporu działająca na klocek ze strony cieczy równa się sile ciężkości działającej na klocek. Po zapisaniu tej równości i następnie podstawieniu w miejsce objętości cieczy wypartej przez klocek ułamka objętości klocka znajdującego się pod jej powierzchnią dostaniemy szukaną wartość gęstości cieczy.

Wartość siły wyporu zależy od masy płynu wypartego przez dane ciało oraz od przyspieszenia grawitacyjnego, którego wartość jest proporcjonalna do masy obiektu przyciągającego to ciało. Masa Ziemi jest większa od masy Księżyca, zatem przyspieszenie grawitacyjne na Ziemi jest większe niż na Księżycu. Oznacza to, że siła wyporu na Księżycu jest mniejsza niż na Ziemi.

Siła wyporu działająca na ciało ze strony płynu zależy m.in. od masy płynu wypartego przez to ciało. Masę płynu możemy przedstawić jako iloczyn gęstości i objętości płynu. Zgodnie z treścią pytania wszystkie kulki są całkowicie zanurzone w wodzie, zatem objętość wypartego płynu równa się objętości kulek. Ponieważ wszystkie kulki mają jednakowy promień, dlatego też każda z kulek wypełnia taką samą objętość (która nie zależy od tego czy kulka jest pełna, czy też wydrążona w środku). Oznacza to, że siła wyporu działająca na każdą z kulek musi mieć wobec tego jednakową wartość.

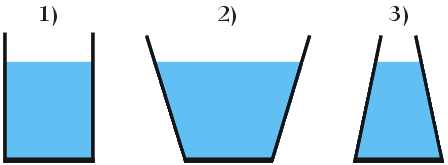
Siła parcia równa się iloczynowi ciśnienia p  oraz pola powierzchni S, na które działa. Wszystkie naczynia mają jednakowe dna, zatem pole powierzchni S  dna jest identyczne we wszystkich naczyniach. Z podobną sytuacją mamy do czynienia w przypadku ciśnienia p. Wartość ciśnienia hydrostatycznego wywieranego na dno naczynia zależy tylko i wyłącznie od wysokości słupa cieczy. Nie zależy ani od wymiarów, ani od kształtu naczynia. Ponieważ poziom wody jest jednakowy we wszystkich naczyniach, zatem ciśnienie p  jest takie samo w każdym z naczyń. Taka sama wartość S  oraz p  dla każdego z trzech przypadków oznacza, że siła z jaką woda działa na dno naczynia jest jednakowa we wszystkich naczyniach.