Test: Energia w ruchu harmonicznym – poziom łatwy
Zależność energii kinetycznej od wychylenia ciała drgającego ruchem harmonicznym prawidłowo przedstawia rysunek:
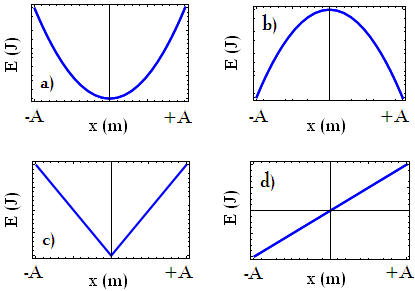
Zobacz energia w ruchu harmonicznym.
Zależność energii potencjalnej od wychylenia ciała drgającego ruchem harmonicznym prawidłowo przedstawia rysunek:
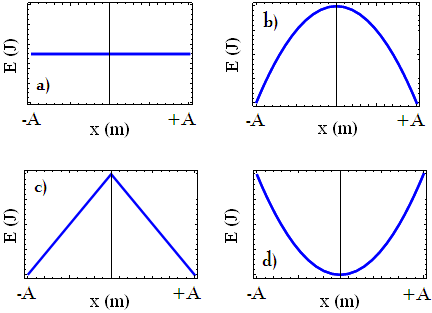
Zobacz energia w ruchu harmonicznym.
Maksymalny pęd ciała wykonującego drgania harmoniczne wynosi p = 10-3 kg ⋅ m/s. Wiedząc, że masa ciała m = 0,02 kg, oblicz ile wynosi jego energia potencjalna w punkcie maksymalnego wychylenia z położenia równowagi.
Aby rozwiązać to zadanie należy zauważyć dwie rzeczy:
a) maksymalny pęd p ciała, podobnie jak energia kinetyczna Ek , osiągany jest w punkcie położenia równowagi (x = 0 m) ciała drgającego harmonicznie. Energia całkowita Ec ciała w tym punkcie jest równa energii kinetycznej ciała: $E_c = E_k = \frac{p^2}{2 m}$,
b) w punkcie maksymalnego wychylenia ciała z położenia równowagi energia potencjalna Ep przyjmuje maksymalną wartość, w związku z czym $E_c = E_p$.
Porównując stronami obydwa wzory, dostaniemy:
$$E_p = \frac{p^2}{2 \hspace{.05cm} m} = 25 \cdot 10^{-6} \hspace{.05cm} \textrm{J}$$Działając na sprężynę siłą o wartości 20 N powodujemy jej wydłużenie o 0,2 m. Jeżeli na takiej sprężynie zawiesimy ciężarek o masie 1 kg i wprawimy go w ruch drgający, częstość kołowa drgań ω będzie równa:
Aby wyznaczyć częstość kołową drgań ω układu sprężyna - ciężarek skorzystamy ze wzoru $k = m \hspace{.05cm} \omega^2$ (zobacz: Siła w ruchu harmonicznym). Stała sprężystości k sprężyny nie jest znana. Możemy ją jednak wyznaczyć ze wzoru $F = \hspace{.1cm} - \hspace{.05cm} k \hspace{.05cm} x$, ponieważ znamy reakcję sprężyny (zmiana długości) na przyłożoną do niej siłę. Po przekształceniu wzoru na siłę względem stałej k i pominięciu znaku minus (interesuje nas wartość reakcji sprężyny na działającą siłę), otrzymamy:
$$k = \frac{F}{x}$$Tak więc:
$$m \hspace{.05cm} \omega^2 = \frac{F}{x}$$Po przekształceniu powyższego wzoru względem częstości kołowej ω, dostaniemy:
$$\omega = \sqrt{\frac{\mathstrut F}{m \hspace{.05cm} x}} = 10 \hspace{.05cm} \textrm{s}^{-1}$$W położeniu równowagi całkowita energia drgań harmonicznych ciała odpowiada wartości jego energii kinetycznej E. Jeżeli wychylenie ciała będzie równe x = A /2, to jego energia kinetyczna będzie wynosić:
Wiemy, że w położeniu równowagi energia kinetyczna E ciała drgającego ruchem harmonicznym odpowiada jego całkowitej energii drgań Ec , dlatego
$$E = E_c = \tfrac{1}{2} \hspace{.05cm} k \hspace{.05cm} A^2$$Gdy wychylenie ciała będzie równe $x = \frac{A}{2}$, wówczas jego całkowita energia drgań będzie wynosić $E_c = E_p + E$, gdzie Ep to energia potencjalna drgań ciała równa
$$E_p = \tfrac{1}{2} \hspace{.05cm} k \hspace{.05cm} x^2$$Przekształcając wyrażenie na energię całkowitą względem energii kinetycznej, dostaniemy:
$$E = E_c \hspace{.1cm} - \hspace{.05cm} E_p = \tfrac{1}{2} \hspace{.05cm} k \hspace{.05cm} A^2 \hspace{.1cm} - \hspace{.05cm} \tfrac{1}{2} \hspace{.05cm} k \hspace{.05cm} \tfrac{A^2}{4}$$Po wykonaniu obliczeń, uzyskamy:
$$E_k = \tfrac{1}{2} \hspace{.05cm} k \hspace{.05cm} \tfrac{3 \hspace{.05cm} A^2}{4}$$Ponieważ $E_c = \tfrac{1}{2} \hspace{.05cm} k \hspace{.05cm} A^2$, zatem:
$$E = \tfrac{3}{4} \hspace{.05cm} E_c$$Ciało wykonuje drgania harmoniczne o amplitudzie A i okresie T. Jeżeli okres drgań zmaleje trzykrotnie, a amplituda nie ulegnie zmianie to maksymalna energia kinetyczna ciała:
Gdy ciało drgające ruchem harmonicznym osiąga maksymalną wartość energii kinetycznej, jego energia potencjalna wynosi 0 J. Oznacza to, że Ekmax = Ec , gdzie Ec to całkowita energia drgań ciała równa:
$$E_c = \tfrac{1}{2} \hspace{.05cm} k \hspace{.05cm} A^2$$Stałą sprężystości k możemy wyrazić jako:
$$k = m \hspace{.05cm} \omega^2 = m \hspace{.05cm} \frac{4 \hspace{.05cm} \pi^2}{T^2}$$Po podstawieniu i skróceniu, dostaniemy:
$$E_{kmax} = E_c = \frac{2 \hspace{.05cm} \pi^2 \hspace{.05cm} m \hspace{.05cm} A^2}{T^2}$$Wzór, który otrzymaliśmy odpowiada sytuacji przed zmianą okresu T. Gdy okres zmaleje trzykrotnie, otrzymamy:
$$E_{kmax2} = \frac{2 \hspace {.05cm} \pi^2 \hspace{.05cm} m \hspace{.05cm} A^2}{\left(\frac{T}{3}\right)^2} = \frac{18 \hspace{.05cm} \pi^2 \hspace{.05cm} m \hspace{.05cm} A^2}{T^2}$$Porównując obydwa wzory możemy stwierdzić, że energia kinetyczna ciała po zmianie okresu T wzrośnie dziewięciokrotnie.
Zależność energii kinetycznej i potencjalnej ciała drgającego ruchem harmonicznym prawidłowo przedstawiają wyrażenia (zakładamy, że wychylenie ciała zmienia się zgodnie z równaniem $x (t) = A \hspace{.05cm} cos \left( \omega \hspace{.05cm} t + \varphi \right)$
Zobacz energia w ruchu harmonicznym.
Jeżeli przez A oznaczymy amplitudę ruchu harmonicznego pewnego ciała, to energia potencjalna równa jest jego energii kinetycznej dla wychylenia x równego (zakładamy, że wychylenie ciała w funkcji czasu zmienia się zgodnie ze wzorem: $x (t) = A \hspace{.05cm} cos \left( \omega \hspace{.05cm} t + \varphi \right)$ ):
Zacznijmy od zapisania warunku równości energii potencjalnej i kinetycznej ciała: Ep = Ek . Wiemy, że:
$$E_p = \tfrac{1}{2} \hspace{.05cm} k \hspace{.05cm} A^2 = \tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} \omega^2 \hspace{.05cm} A^2 \hspace{.05cm} \textrm{cos}^2 \left(\omega \hspace{.05cm} t + \varphi \right)$$oraz, że:
$$E_k = \tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} V^2 = \tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} \omega^2 \hspace{.05cm} A^2 \hspace{.05cm} \textrm{sin}^2 \left(\omega \hspace{.05cm} t + \varphi \right)$$Po przyrównaniu stronami i skróceniu, otrzymamy:
$$\textrm{cos}^2 \left(\omega \hspace{.05cm} t + \varphi \right) = \textrm{sin}^2 \left(\omega \hspace{.05cm} t + \varphi \right)$$Po skorzystaniu z jedynki trygonometrycznej $\textrm{sin}^2 x + \textrm{cos}^2 x = 1$, uzyskamy:
$$2 \hspace{.05cm} \textrm{cos}^2 \left(\omega \hspace{.05cm} t + \varphi \right) = 1$$i w konsekwencji:
$$\omega \hspace{.05cm} t + \varphi = \frac{\pi}{4}$$Znając fazę drgań możemy przystąpić do obliczenia wychylenia:
$$x^2 = \frac{m \hspace{.05cm} V^2}{k} = \frac{m \hspace{.05cm} \omega^2 \hspace{.05cm} A^2 \hspace{.05cm} \rm{cos}^2 \left(\frac{\pi}{4} \right)}{m \hspace{.05cm} \omega^2}$$Po skróceniu i spierwiastkowaniu, dostaniemy:
$$x = \tfrac{\sqrt{2}}{2} \hspace{.05cm} A$$Która z podanych wielkości fizycznych opisujących ruch harmoniczny nie zależy od fazy początkowej fazy drgań φ ?
Zarówno wartość siły, energii potencjalnej, jak i energii kinetycznej ciała drgającego ruchem harmonicznym zależy bezpośrednio, bądź pośrednio od wychylenia ciała x , w związku z czym wielkości te są uzależnione od początkowej fazy drgań φ. Wielkością niezależną od fazy drgań jest energia całkowita, której wartość zależy tylko od stałej sprężystości k oraz amplitudy drgań A: $$E_c = \tfrac{1}{2} \hspace{.05cm} k \hspace{.05cm} A^2$$
Jak zmieni się całkowita energia drgań harmonicznych pewnego ciała, jeżeli okres T oraz amplitudę A drgań zwiększymy czterokrotnie?
Zacznijmy od zapisania wzoru na energię całkowitą w ruchu harmonicznym:
$$E_c = \tfrac{1}{2} \hspace{.05cm} k \hspace{.05cm} A^2 = \tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} \omega^2 \hspace{.05cm} A^2 = \frac{2 \hspace{.05cm} \pi^2 \hspace{.05cm} m \hspace{.05cm} A^2}{T^2}$$Wzór ten opisuje początkową energię całkowitą ciała (przed zmianą T i A ). Po zmianie okresu i amplitudy drgań wzór ten przyjmie następującą postać:
$$E_{c} = \frac{2 \hspace{.05cm} \pi^2 \hspace{.05cm} m \cdot 16 \hspace{.05cm} A^2}{16 \hspace{.05cm} T^2} =\frac{2 \hspace{.05cm} \pi^2 \hspace{.05cm} m \hspace{.05cm} A^2}{T^2}$$Widzimy więc, że energia całkowita ciała nie ulegnie zmianie.

Dodaj komentarz