Test: Mechanika płynów – poziom trudny
Drewniany klocek o gęstości 0,7 g/cm3 pływa częściowo zanurzony w wodzie o gęstości 1000 kg/m3. Jeżeli masa klocka wynosi 0,15 kg, to siła zewnętrzna potrzebna do całkowitego zanurzenia klocka jest równa (g = 10 m/s2):
Pod wpływem zewnętrznej siły przyłożonej do klocka, klocek ulega całkowitemu zanurzeniu. Oznacza to, że:
$$F + F_g = F_{wyp}$$gdzie F - siła zewnętrzna, Fg - siła ciężkości, Fwyp - siła wyporu.
Po wstawieniu w miejsce Fg wyrażenia $m_k \hspace{.05cm} g$ oraz $F_{wyp} = \rho_w \hspace{.05cm} g \hspace{.05cm} \frac{m_k}{\rho_k}$ oraz po przekształceniu powyższego wzoru względem F , dostaniemy:
$$F = F_{wyp} \hspace{.1cm} - \hspace{.05cm} F_g = \rho_w \hspace{.05cm} g \hspace{.05cm} \frac{m_k}{\rho_k} \hspace{.1cm} - \hspace{.05cm} m_k \hspace{.05cm} g = g \left[ \rho_w \cdot \left( \dfrac{m_k}{\rho_k} \right) \hspace{.05cm} - \hspace{.05cm} m_k \right]$$gdzie mk i ρk to odpowiednio masa i gęstość klocka, ρw - gęstość wody.
W szklance w kształcie walca, której pole podstawy wynosi 10 π dm2 znajduje się woda. Do szklanki wrzucono kulkę ołowianą o promieniu 5 cm, która całkowicie zanurzyła się w wodzie. Ciśnienie hydrostatyczne wywierane przez wodę na dno naczynia wzrosło po wrzuceniu kulki o (g = 10 m/s2):
Korzystamy ze wzoru na ciśnienie hydrostatyczne. Przed wrzuceniem kulki do szklanki ciśnienie hydrostatyczne p0 wynosiło:
$$p_0 = \rho_w \hspace{.05cm} g \hspace{.05cm} h$$Wysokość słupa wody nie jest znana, jednak korzystając ze wzoru na objętość walca możemy ją wyrazić jako:
$$h = \dfrac{V_w}{S}$$gdzie Vw to objętość wody, S - pole podstawy szklanki.
Po wrzuceniu kulki poziom wody nieznacznie się zwiększył, zatem ciśnienie hydrostatyczne po wrzuceniu kulki wynosi teraz:
$$p_1 = \rho_w \hspace{.05cm} g \cdot \left( \dfrac{V_w + V_k}{S} \right)$$gdzie Vk to objętość kulki równa $V_k = \frac{4}{3} \hspace{.05cm} \pi \hspace{.05cm} r^3$.
Znając obydwa ciśnienia możemy obliczyć ich różnicę:
$$\Delta \hspace{.03cm} p = p_1 \hspace{.1cm} - \hspace{.05cm} p_0 = \rho_w \hspace{.05cm} g \cdot \left( \dfrac{V_w + V_k}{S} \right) \hspace{.1cm} - \hspace{.05cm} \frac{\rho_w \hspace{.05cm} g \hspace{.05cm} V_w}{S} = \dfrac{\rho_w \hspace{.05cm} g \hspace{.05cm} V_k}{S}$$Do jakiej wysokości h należy nalać jednorodną ciecz do naczynia w kształcie walca, aby siła parcia cieczy na ścianę boczną tego naczynia była równa sile parcia cieczy na dno tego naczynia?
Pole powierzchni podstawy walca wynosi $S = \pi \hspace{.05cm} r^2$. Pole powierzchni ściany bocznej dostaniemy dzieląc walec na dwie równe części. Rozwijając następnie tą część walca na płaszczyźnie dostaniemy prostokąt o bokach h i π r (połowa obwodu koła). Podstawiając następnie obydwa pola powierzchni do wzoru na siłę parcia (F = p S ) dostaniemy szukaną wysokość wody w walcu.
Drewniana kulka o masie 20 g przymocowana jest sznurkiem do dna zbiornika wypełnionego wodą o gęstości 1000 kg/m3. Jeżeli objętość kulki wynosi 40 cm3, to siła naprężenia sznurka jest równa (g = 10 m/s2):
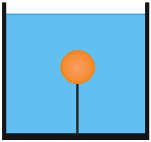
Aby obliczyć siłę naprężenia sznurka należy skorzystać z drugiej zasady dynamiki Newtona. Kulka znajduje się w spoczynku, zatem:
$$F_n + F_g = F_{wyp}$$gdzie Fn - siła naprężenia sznurka, Fg - siła ciężkości działająca na kulkę, Fwyp - siła wyporu działająca na kulkę.
Po podstawieniu w miejsce Fg wyrażenia $m_k \hspace{.05cm} g$ oraz $F_{wyp} = \rho_w \hspace{.05cm} V_k \hspace{.05cm} g$, dostaniemy:
$$F_n = F_{wyp} \hspace{.1cm} - \hspace{.05cm} F_g = \rho_w \hspace{.05cm} V_k \hspace{.05cm} g \hspace{.1cm} - \hspace{.05cm} m_k \hspace{.05cm} g = g \left( \rho_w \hspace{.05cm} V_k \hspace{.1cm} - \hspace{.05cm} m_k \right)$$gdzie ρw - gęstość wody, Vk - objętość kulki, mk - masa kulki.
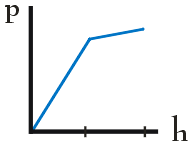
W pewnym naczyniu znajdują się dwie ciecze o gęstościach ρ1 i ρ2, przy czym ρ1 > ρ2. Zależność ciśnienia hydrostatycznego p od głębokości h prawidłowo przedstawia wykres:
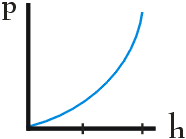
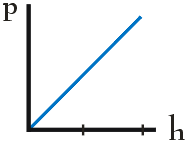
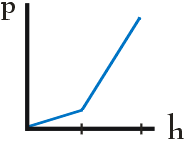
Dwa sześcienne klocki wykonane z dwóch różnych metali: pierwszy - z ołowiu o gęstości 11300 kg/m3, drugi - z niklu o gęstości 8725 kg/m3 zanurzono w wodzie o gęstości 1000 kg/m3. Pomiary ciężaru każdego z klocków wykonane w wodzie wykazały, że ciężar obydwu klocków jest jednakowy. Oznacza to, że stosunek objętości pierwszego klocka do objętości klocka drugiego wynosi:
Ciężar klocków zmierzony w wodzie to ich ciężar pozorny. Wiemy, że ciężar pozorny obydwu klocków jest jednakowy, zatem korzystając z definicji ciężaru pozornego, dostaniemy:
$$Q_1 \hspace{.1cm} - \hspace{.05cm} F_{wyp1} = Q_2 \hspace{.1cm} - \hspace{.05cm} F_{wyp2}$$gdzie Q1 i Q2 to ciężar odpowiednio pierwszego oraz drugiego klocka, Fwyp1 i Fwyp2 - siła wyporu działająca odpowiednio na pierwszy oraz drugi klocek.
Po wstawieniu w miejsce ciężaru i siły wyporu odpowiednich wyrażeń i po przekształceniu otrzymanego równania względem objętości obydwu klocków, dostaniemy ogólny wzór pozwalający obliczyć stosunek tych dwóch objętości:
$$\frac{V_1}{V_2} = \frac{\rho_2 \hspace{.1cm} - \hspace{.05cm} \rho_w}{\rho_1 \hspace{.1cm} - \hspace{.05cm} \rho_w}$$Ile wynosi objętość ciała, które w wodzie waży o 2 N mniej niż w powietrzu? Gęstość wody wynosi 1000 kg/m3, gęstość powietrza - 1,2 kg/m3.
Korzystamy z definicji ciężaru pozornego. Zapisujemy odpowiednie równanie dla przypadku, w którym ciało znajduje się w wodzie oraz dla przypadku, w którym ciało znajduje się w powietrzu. Z warunków zawartych w treści zadania, mamy:
$$Q_{poz,p} = Q_{poz,w} + 2 \hspace{.05cm} \textrm{N}$$gdzie Qpoz,p to ciężar pozorny ciała w powietrzu, Qpoz,w - ciężar pozorny ciała w wodzie.
Po podstawieniu w miejsce ciężarów pozornych odpowiednich wyrażeń dostaniemy objętość ciała równą:
$$V = \frac{2}{\rho_w \hspace{.05cm} g \hspace{.1cm} - \hspace{.05cm} \rho_p \hspace{.05cm} g}$$gdzie ρw - gęstość wody, ρp - ciężar powietrza.
Na głębokości h = 2 m poniżej poziomu wody o gęstości 1000 kg/m3 znajduje się drewniana kulka o gęstości 800 kg/m3. Jeżeli kulkę tą swobodnie puścimy, wysokość na jaką wyskoczy ponad poziom wody wyniesie:
Aby obliczyć wysokość na jaką z wody wyskoczy kulka należy skorzystać z drugiej zasady dynamiki Newtona oraz ze wzorów na prędkość i drogę w ruchu jednostajnie przyspieszonym. Na początku należy obliczyć prędkość kulki w momencie dotarcia do powierzchni wody. Prędkość ta będzie jednocześnie prędkością końcową po przebyciu drogi w wodzie oraz prędkością początkową "nowego" ruchu - od powierzchni wody do wysokości wzniesienia się nad powierzchnię wody. Po zapisaniu i przekształceniu wzorów na prędkość oraz drogę w ruchu jednostajnie przyspieszonym dostaniemy szukaną wysokość równą:
$$s = h \cdot \left( \frac{\rho_w}{\rho_d} \hspace{.1cm} - \hspace{.05cm} 1 \right)$$Dwa identyczne naczynia wypełniono wodą o gęstości ρ, do tej samej wysokości równej h. Następnie naczynia te umieszczono w dwóch windach. Pierwsza z nich porusza się do góry z przyspieszeniem a = 2/3 g, druga z nich - w dół z przyspieszeniem a = 1/3 g. Jeżeli pole przekroju każdego z naczyń wynosi S, to różnica ciśnień wywieranych na dno naczynia znajdującego się w pierwszej oraz w drugiej windzie wynosi:
Ciśnienie hydrostatyczne równa się iloczynowi gęstości płynu ρ, wysokości słupa płynu h oraz przyspieszenia grawitacyjnego g. Wiemy, że poziom wody w obydwu naczyniach jest jednakowy. Wiemy także, że naczynia te znajdują się w dwóch różnych windach poruszających się w przeciwnych kierunkach z różnym przyspieszeniem.
W pierwszym przypadku, winda porusza się w górę z przyspieszeniem a = 2/3 g, zatem całkowite przyspieszenie, z jakim porusza się winda (a więc również i naczynie) wynosi g + 2/3 g (aby otrzymać tą wartość należy skorzystać z drugiej zasady dynamiki Newtona).
W drugim przypadku winda porusza się w dół z przyspieszeniem a = 1/3 g, zatem w tym przypadku całkowite przyspieszenie układu wynosi g - 1/3 g. Po podstawieniu tych przyspieszeń do wzoru na ciśnienie hydrostatyczne i następnie obliczeniu różnicy tych ciśnień otrzymamy wynik: ρ g h.
Dwa drewniane, sześcienne klocki pływają zanurzone do połowy w pewnej cieczy. Bok małego klocka wynosi a, dużego - 4 a. Działając siłą na górne ściany klocków, spowodowano ich całkowite zanurzenie. Zanurzenie większego klocka wymagało wykonania pracy
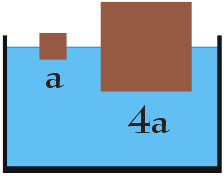
Aby obliczyć pracę potrzebną do zanurzenia małego oraz dużego klocka musimy znać wartość siły, jaka musi działać na powierzchnię górnej ściany klocka oraz odległość o jaką musi przemieścić się klocek, aby uległ całkowitemu zanurzeniu w cieczy. Wiemy, że obydwa klocki zanurzone są do połowy, zatem przemieszczenie mniejszego klocka wynosi 1/2 a, a większego 2 a. Aby obliczyć wartość siły jaką musimy przyłożyć do klocka, aby spowodować jego zanurzenie należy skorzystać z drugiej zasady dynamiki Newtona. Po zapisaniu odpowiednich równań powinniśmy dostać:
$$F_1 = a^3 \hspace{.05cm} g \left( \rho_w \hspace{.1cm} - \hspace{.05cm} \rho_k \right)$$oraz:
$$F_2 = 64 \hspace{.05cm} a^3 \hspace{.05cm} g \left( \rho_w \hspace{.1cm} - \hspace{.05cm} \rho_k \right)$$Po podstawieniu siły i przemieszczenia do wzoru na pracę oraz po wykonaniu obliczeń otrzymamy szukaną wartość stosunku pracy równą 256.

Dodaj komentarz