Energia w ruchu harmonicznym

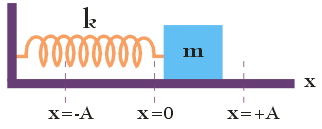
Gdy przemieszczenie układu składającego się z klocka o masie m  i sprężyny o stałej sprężystości k  (zobacz rysunek), drgającego ruchem harmonicznym jest liniowo proporcjonalne ze znakiem minus do siły, która ten ruch wywołała, wówczas układ taki nazywamy liniowym oscylatorem harmonicznym. Zależność F(t)  dla takiego układu przedstawiono w artykule Siła w ruchu harmonicznym. W tym artykule zajmiemy się opisem energii mechanicznej w ruchu harmonicznym. Przekonasz się, że energia mechaniczna liniowego oscylatora harmonicznego zmienia się z energii kinetycznej w energię potencjalną i odwrotnie, przy czym suma tych dwóch energii przez cały czas trwania ruchu pozostaje stała (zakładamy brak jakichkolwiek sił tarcia działających na układ).

Energia potencjalna i energia kinetyczna w ruchu harmonicznym – wzór

Na początku założymy, że masa układu klocek – sprężyna związana jest tylko i wyłącznie z masą m  klocka, z kolei stała sprężystości k  ze sprężyną. W takim przypadku wartość energii potencjalnej sprężystości E_p(t)  zależy tylko od stopnia rozciągnięcia lub ściśnięcia x(t)  sprężyny, natomiast energia kinetyczna E_k(t)  – od prędkości klocka V(t). W oparciu o powyższe założenia energię potencjalną sprężystości sprężyny możemy wyrazić jako:

$$E_p (t) = \tfrac{1}{2} \hspace{.05cm} k \hspace{.05cm} x^2 (t) = \tfrac{1}{2} \hspace{.05cm} k \hspace{.05cm} A^2 \hspace{.05cm} \textrm{cos}^2 \left( \omega \hspace{.05cm} t + \varphi \right)$$

z kolei energię kinetyczną klocka poprzez:

$$E_k (t) = \tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} V^2 (t) = \tfrac{1}{2} \hspace{.05cm} m \hspace{.05cm} A^2 \hspace{.05cm} \omega^2 \hspace{.05cm} \textrm{sin}^2 \left( \omega \hspace{.05cm} t + \varphi \right)$$

gdzie w miejsce x(t)  i V(t)  wstawiliśmy zależność opisującą odpowiednio przemieszczenie oraz prędkość ciała w ruchu harmonicznym.

Jeżeli częstość kołową ω  wyrazimy jako:

$$\omega = \sqrt{\frac{\mathstrut k}{m}}$$

i podstawimy do wyrażenia na E_k(t), dostaniemy:

$$E_k (t) = \tfrac{1}{2} \hspace{.05cm} k \hspace{.05cm} A^2 \hspace{.05cm} \textrm{sin}^2 \left( \omega \hspace{.05cm} t + \varphi \right)$$

Energia całkowita w ruchu harmonicznym – wzór

Suma wyrażeń E_p(t)  i E_k(t)  pozwoli nam uzyskać wzór na całkowitą energię mechaniczną E  liniowego oscylatora harmonicznego:

$$E = E_p (t) + E_k (t) = \tfrac{1}{2} \hspace{.05cm} k \hspace{.05cm} A^2 \left[ \textrm{cos}^2 \left( \omega \hspace{.05cm} t + \varphi \right) + \textrm{sin}^2 \left( \omega \hspace{.05cm} t + \varphi \right) \right] = \tfrac{1}{2} \hspace{.05cm} k \hspace{.05cm} A^2$$

(aby otrzymać powyższą zależność skorzystaliśmy ze wzoru jedynki trygonometrycznej: $\textrm{cos}^2 \left( \omega \hspace{.05cm} t + \varphi \right) + \textrm{sin}^2 \left( \omega \hspace{.05cm} t + \varphi \right) = 1$).

Zgodnie z powyższym wyrażeniem całkowita energia mechaniczna liniowego oscylatora harmonicznego przez cały czas trwania jego ruchu pozostaje stała. Możesz się o tym przekonać analizując poniższe wykresy, na których przedstawiono zależność energii potencjalnej sprężystości, energii kinetycznej oraz całkowitej energii mechanicznej oscylatora liniowego w funkcji czasu t  i przemieszczenia x.

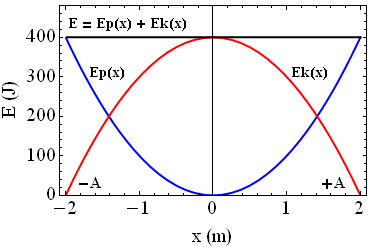
Zwróć uwagę, że zgodnie z tym co napisaliśmy na początku tego artykułu, energia całkowita w funkcji czasu zmienia się z energii kinetycznej w energię potencjalną i odwrotnie, przy czym całkowita energia mechaniczna układu pozostaje stała. Dodatkowo, gdy klocek i sprężyna znajdują się w położeniu równowagi (x  = 0), całkowita energia układu odpowiada energii kinetycznej klocka, a gdy x = ± A  – energia układu związana jest tylko i wyłącznie z energią potencjalną sprężystości sprężyny.